一道竞赛试题的多解探究及其推广

文帅 李乾瑞 梁明端

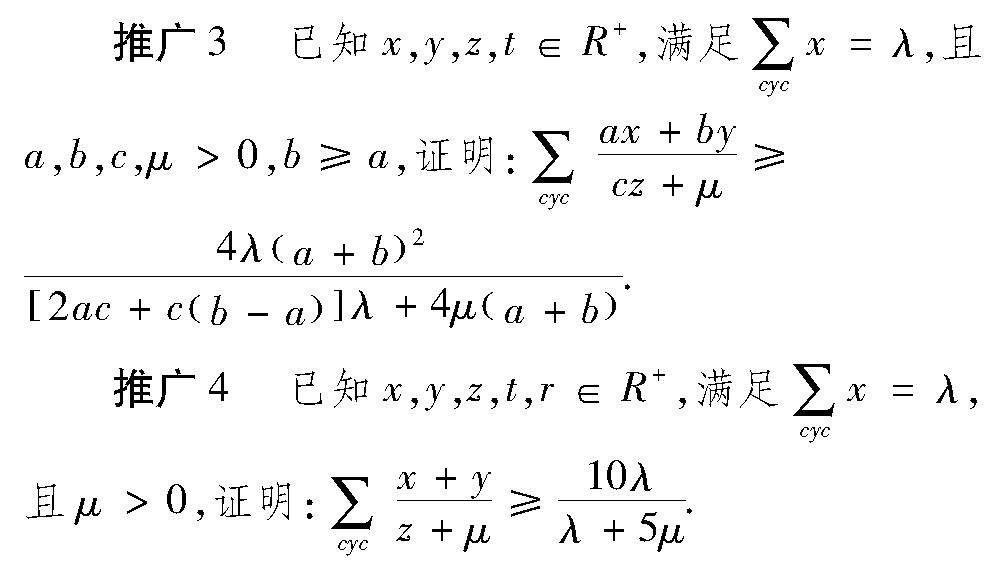
1.试题呈现

分析：这是2023年愛尔兰奥林匹克竞赛试题的一道不等式证明题，其中不等式的左侧是以循环和的形式呈现，具有数学的美感，本文对该题进行解法探究，并对其进行变式和推广.

2．解法探究

评注：此证法借助于权方和不等式与基本不等式的推广，使不等式得以证明.

评注：此证法利用函数的凹凸性与琴生不等式，将不等式问题转化为求函数最值问题，从而使得不等式得以证明.

评注： 此证法利用切线的性质，将不等式问题转化为求函数最值问题，从而使不等式得以证明.

评注：此变式是在试题的基础上改变题设条件而得到的，其证明方法是结合权方和不等式与基本不等式的推广，使得不等式得以证明.

4.试题推广

推广是数学研究中极为重要的手段之一，笔者将试题中的未知数a，b，c改写为x，y，z来加以研究.

4.1 对不等式中所含数字及系数一般化

4.3 增加不等式中未知数的个数

4.4 改变不等式的结构

推广6 已知x，y，z∈R+，n≥1，证明：∑cycxn+ynzn+xyn2≥3.

上述推广是在试题的基础上改变不等式结构以及题设条件而得到的，下面列举推广3和推广6的证明，其它推广的证明过程不再叙述.

推广，对于数学学习、数学竞赛和数学研究有着十分重要的意义.在数学学习中，推广可以加强观察、分析、比较、综合、概括、归纳、类比和发现的能力，拓展不同的解题思路，提升创造性的思维.在数学竞赛中，推广可以激发学习兴趣与求知欲，引领新的发现. 在数学研究中，推广可以产生新问题与新方法，加深自身对问题的认识与理解［1］.

参考文献

［1］朱华伟，张景中.论推广［J］.数学通报，2005（04）：55-57+28.