多证源于结构 推广顺其自然
2024-06-11 03:51:03张庆
中学数学研究 2024年6期
张庆

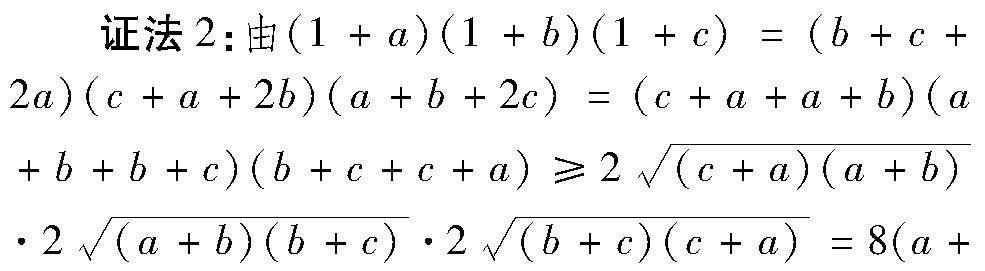

由证法1知(1-a)(1-b)(1-c)=(b+c)(c+a)(a+b),因此,把(1+a)(1+b)(1+c)中的1逆代后,重新拆分变形,可以获得证法2.
不等式(1)的左边是三个因式的积,右边是一个立方根项,如果把左边先变形为立方根的形式,那么可以获得证法3.
成立.
以上三种证法都是从左边去证明右边的,如果反而行之,那么可以获得证法4.
点评:上述四种不同的证法,都是充分挖掘了不等式(1)的结构特点,入手自然有据,思路清晰有理,前三种证法是常规性思维,由左到右循序渐进,后一种证法采取了逆向思维,过程简捷漂亮,由此彰显了不等式(1)的内在价值.
点评:对于不等式(1),分别从改变常数项和变量幂指数两个方面得到推广1和推广2,
其证法思路与上述证法2和证法4完全一致,尤其是推广2,如果没有证法4的浮出,那么很难给出这么精彩的证明.因此,多視角、多层次解决数学问题,对于问题的推广和引申极为重要.
猜你喜欢
小学生作文·小学低年级适用(2023年2期)2023-11-01 11:04:02
数理天地(高中版)(2023年5期)2023-07-06 03:16:12
中学生数理化·七年级数学人教版(2023年3期)2023-03-21 00:45:16
物理学报(2022年1期)2022-01-19 04:44:04
考试与评价·高一版(2020年1期)2020-10-26 02:25:46
山西教育·招考(2019年6期)2019-09-10 07:22:44
中学生数理化·七年级数学人教版(2018年3期)2018-05-30 06:58:18
中学生数理化·七年级数学人教版(2017年3期)2018-01-20 12:45:56
军事运筹与系统工程(2017年1期)2017-07-31 18:19:01
考试周刊(2016年99期)2016-12-26 10:54:30

