落实主体地位 构建生命课堂

周晓琳

在数学学习过程中，学生常用“枯燥”、“抽象”、“难学”来评价数学学习，表现为学习兴趣不高，学习效率低下.出现这一现象大多与教师的教学相关，不少教师的课堂教学，常常独占课堂，忽视学生的主体地位，使得学生在课堂上不能表达自己的所思、所想，限制学生学习能力和思维能力的发展.因此，在数学教学中，教师要将课堂还给学生，充分发挥学生的主体价值，以确保促进学生全面发展的数学教学目标的落实.本文笔者以一道解析几何题的教学为例，谈谈如何将课堂还给学生，提升教学有效性的一些思考.

一、问题呈现

120°时，求证：（i）点P一定在经过A、B、C三点的圆M上；（ii）PA=PB+PC.

二、教学过程

1.互动交流，启迪思维

师：若想证明一点在一定圆上，常用的方法有哪些？

生1：证明该点到圆心的距离等于半径.

生2：证明该点的坐标适合圆的方程.

师：还有其他方法吗？

生3：证明凸四边形的对角互补.

师：非常好，生1和生2的方法本质上是一致的，接下来请大家选择适合自己的方案给出分析过程.

设计意图：教学中，教师将问题进行拆分，首先让学生思考证明一点在一定圆上的方法，以此降低思维难度，唤醒学生的原认知，帮助学生探寻解题的突破口.

2.交流展示，拓宽视野

教学中，教师预留充足的时间让学生独立思考，并让学生选择适合自己的解题方案.几分钟后，大多数学生已经形成解题思路，教师重视展示学生的解题方法.

师：谁来说一说，你是如何证明点P一定在经过A、B、C三点的圆M上的呢？

师：很好，还有其他方法吗？

生5：我是用生3的思路证明的.由β－α=120°可知，点P在x轴下方，如图1，只需要证明∠BAC+∠BPC=180°即可.由已知可知∠BCP=α，∠CBP=180°－β.所以∠BPC=180°－（∠BCP+∠PBC）=180－（α+180°－β）=β－α=120°，又因为ΔABC是正三角形，所以∠BAC=60°，所以∠BAC+∠BPC=180°，问题获证.

师：很好，生4是将几何问题代数化，根据已知将α、β转化为正切函数，通过证明点P的坐标适合圆的方程，证明了结论；生5直接运用几何法解决问题，通过“对角互补的四边形一定是圆的内接四边形”这一性质，证明了结论.这样从“数”和“形”两个角度解决问题，彰显了数形结合的魅力.

设计意图：教学中，教师尊重学生、相信学生，鼓励学生运用自己喜欢的方式解决问题，充分体现了以生为本的教学理念.同时通过互动交流，拓宽学生的视野，丰富学生的基本活动经验，提高学生分析和解决问题的能力.

3.小组合作，激发思维

经历以上自主探究过程，学生的学习兴致高涨，教师将主动权交给学生，引导学生通过小组合作的方式共同探究（ii）的解法.教师预留时间让各小组充分交流，然后展示学生的交流成果.

师：如何证明PA=PB+PC？你想如何表示线段PA、PB、PC的长度呢？

生6：运用两点间的距离公式可以分别表示它们的长度.

生7：也可以将线段长度放在三角形中，运用正、余弦定理表示.

师：大家都说得非常好，请各组结合上面的分析，给出具体解法.

（学生积极运算、积极交流，课堂氛围活跃）

师：很好，该方法思路简单，易于理解，不过对运算能力的要求较高，大家在计算时一定要细心.还有其他方法嗎？

生11：我是将PA、PB、PC放在三角形中研究，利用正弦定理来处理.

生13：我是利用几何法证明的.

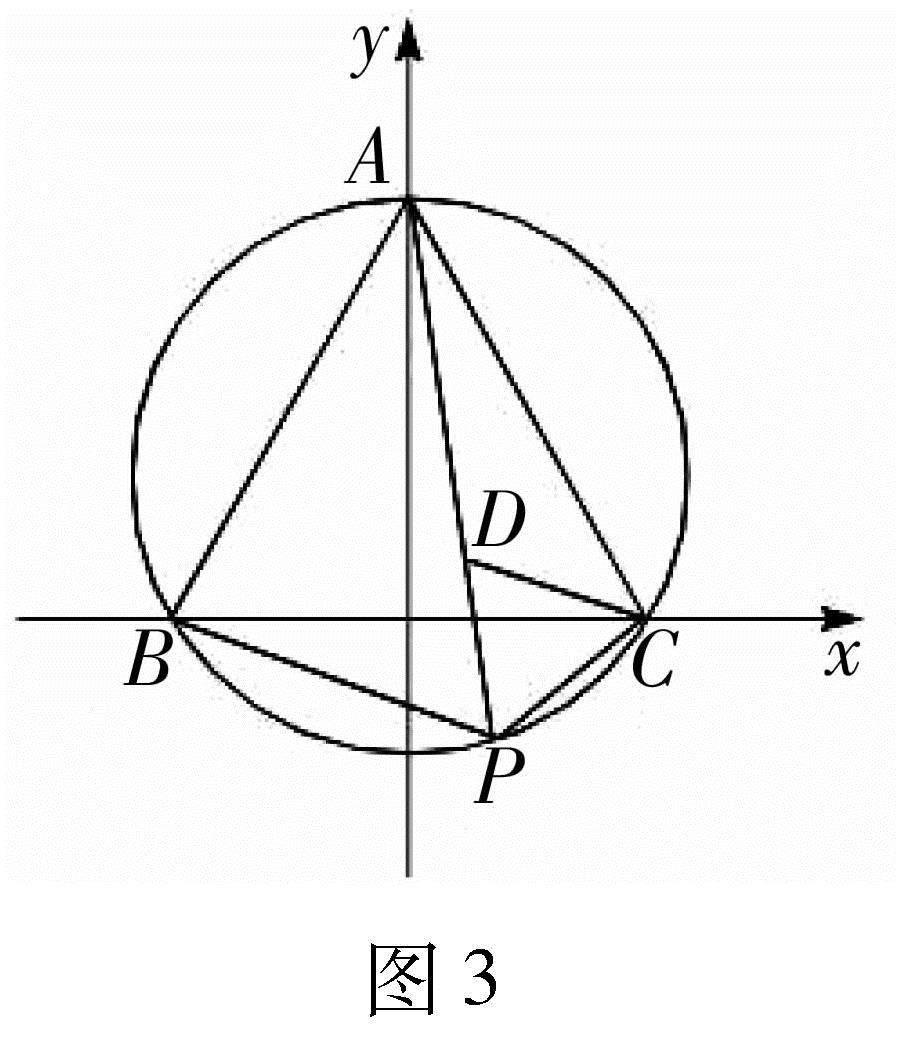
如图3，在线段PA上截取PD=PC.因为ΔABC是正三角形，所以有∠ABC=60°.根据同弧所对圆周角相等，易证∠PAC=PBC，∠DPC=60°，又PD=PC，所以ΔDPC也为正三角形.所以DC=PC，∠PDC=60°，∠ADC=120°，又因为β－α=120°，所以∠BPC=120°，∠BPC=∠ADC，图3∠ACD=∠BCP，又AC=BC，DC=PC，所以ΔADCΔBPC，AD=PB，又PD=PC，所以PA=AD+PD=PB+PC.

师：能想到用初中所学的截长补短法来证明，非常棒.对于同一题目，从不同角度观察，往往会得到不同的结果，在平时练习中，我们要尝试从不同角度去分析，这样往往可以获得柳暗花明的效果.

设计意图：教学中，教师启发学生以“长度的表示”这一核心知识点为抓手，寻求不同的解决方案.学生通过交流分别从代数、三角、几何的角度解决了问题，充分展示了解题方法的多样性.在此过程中，教师让学生以小组为单位，通过相互启发、相互补充，让不同思维碰撞出火花，顺利地突破了这一难点问题，促进了学生解题能力的提升和思维能力的发展.

三、教学思考

在本案例教学中，教师相信学生，放手让学生思考、交流、实践，使课堂呈现了勃勃生机，让学生充分体会了数学探究的兴趣，使学生的自信心和实践能力得到了有效的锻炼，有利于发展学生的综合能力和综合素养.

事实上，真正有效的课堂离不开学生的参与，教学中要提供机会让学生多参与活动，而不是教师在讲，学生在听.教师要变“主宰”为“主导”，既要提供时间和空间让学生独立思考和合作交流，也要给予适时的指导，让学生充分体验成功的快乐，增加学生对数学的热爱，提升课堂教学效果.

总之，在课堂教学中，尤其在解题教学中，不应该是直接讲授，更多的应该是启发和点拨，将思考、展示、交流的空间还给学生，让学生真正地走进数学课堂，获得可以持续学习的必备品格和关键能力，提升学生数学核心素养.