高中数学教学中学生直观想象素养的培养策略探析

田自上

【摘要】新课程改革背景下，教师应当重视学生的学习实践，通过多元化的教学方式，将抽象的知识点以直观、形象的形式呈现出来，这对培养学生良好的直观想象素养具有积极的影响作用.鉴于此，文章以“发展学生的直观想象核心素养，提高学生运用数学知识解决问题的综合能力”作为研究目的，通过新旧对比、创设情境、信息技术、构建模型、数形结合、实验探究、综合评价等教学策略，培养高中学生的直观想象核心素养.

【关键词】高中数学；直观想象；培养对策

直观想象是高中数学核心素养的主要组成，要求学生能借助空间分析事物的形态变化、运动规律、位置关系.同时，也能通过图形的基本描述，解决复杂的数学问题，构建与问题有关的数学模型，将数与形的关系直观呈现出来，探究合理的解析思路.对于课程改革背景下的高中数学教学而言，培养学生良好的直观想象核心素养，对其思维能力与应用能力的发展均具有重要意义.

一、对比新旧课程，加深知识联系

在高中数学课程中，新知识与旧知识之间往往存在千丝万缕的关系.尤其对数函数和指数函数，其图像有着较高的相似度.笔者认为，在学习新的函数课程时，教师可以将已学过的数学课程作为切入点，让学生通过对比两种函数的概念、图像、结构等特点，更好地加深学习认知.这样既能顺应学生的数学认知特点，也能体现从特殊到一般的教学思想，帮助学生深入理解函数的基本性质，培养学生的数学直观想象素养.

以湘教版高一数学必修第一册第3章“函数的概念与性质”的教学为例，教师在讲解“函数的单调性”这一知识点时，先带领学生温习指数函数、对数函数的图像，并针对二者的函数公式y=ax与y=logax，分别规定a>1以及01时，指数函数与对数函数的图像均有“y随x增大而增大”的特点，当0

二、创设教学情境，结合生活元素

由于高中阶段的数学知识比较抽象难懂，教师如果沿袭陈旧的教学思路，很容易使学生产生枯燥乏味的学习感觉.若想培养学生形成良好的直观想象素养，教师应当通过情境教学法，结合富有趣味性、真实性的生活元素，将复杂、抽象的数学概念形象化，充分提高学生的学习代入感.

仍以“函数的单调性”教学为例，教师可以引入以下情境：图1所呈现的是某市一天内的气温变化曲线图.通过这张图片，你是否能准确叙述气温的变化特点？天气预报是学生日常生活中经常接触的事物，每天气温的波动情况也是学生十分关注的事情.通过生活情境的导入，学生能结合自己的实际经历，体会气温在不同时间段内的升降特点.在此基础上，教师再将变化趋势与函数图像的单调性相结合，以加强学生的感性认知，为后续的理性学习做好准备.由此可见，在教学中将抽象的数学知识结合生活实际，不仅可以加深学生的学习印象，还可以充分培养学生的直观想象素养.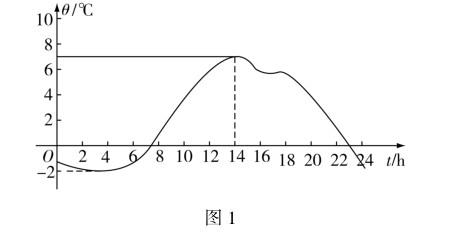

三、运用信息技术，优化学习体验

随着素质教育的深入实施，高中数学教师若想落实核心素养教育任务，应当摒弃陈旧落后的教学思路，重视学生的学习体验.信息化教学具有良好的直观性，可以变静为动，迅速吸引学生的学习注意力.对此，教师在实际教学中，应合理运用信息技术，将抽象难懂的数学知识层层剖析，充分优化学生的学习体验，培养学生的数学直观想象素养.

四、制作实物模型，引导空间想象

高中阶段，几何课程需要从二维层面过渡到三维层面.学生在接触立体几何的课程时，需要改变平面几何的思维方式，通过良好的空间想象，分析物体的位置关系.然而在实际教学中，教师发觉许多学生欠缺良好的空间想象能力，导致学生学习该部分课程会产生举步维艰的感觉.对此，教师要引导学生亲手制作实物模型，根据模型代入立体几何的知识要点，在类比分析的过程中强化直观想象能力.

例如，教師在教学湘教版高一数学必修第二册第4章“立体几何初步”的课程时，先和学生一起制作了圆锥模型，并剪开圆锥侧面，让学生观察展开图.学生可以明确了解到，圆锥侧面的展开图是一个扇形.以此为基础，教师还要提醒学生从二维角度观察展开图，从三维角度观察圆锥模型，剖析平面几何与立体几何之间的转化关系.经过观察，学生不难发现，圆锥侧面在展开之后，其底面圆的周长恰好与扇形的弧长相等.由此，在转化过程中，学生就能迅速把握其中的数据变化特点.

五、注重数形结合，剖析经典例题

直观想象核心素养是高中生挖掘问题、提出问题、分析问题、解决问题的主要手段，可以帮助学生在探索新知识的过程中形成良好的论证思路，完成综合性的逻辑推理，构建出形象、完整的知识体系.想要培养学生良好的直观想象能力，教师不能急于求成，而是要通过针对性的引导，选择合适的数学研究方法，让学生能在解决问题的过程中进行精准的判断和推理.通过实践发现，在高中数学教学中，采用数形结合的方式，搭配经典的数学例题，可以有效促进学生直观想象核心素养的提升.

数形结合思想充分体现了直观想象核心素养的应用.在处理本道例题时，教师有意识地引导学生从图像的角度确定坐标的关系，将题干内容转化成图像中的对应线段，并结合抛物线、直线、圆等方程的基本定义，达成数形转化的目的，充分激发了学生的直观想象学习意识.

六、组织探究实践，深化知识应用

在高中阶段，许多数学课程不再死板套用公式，而是深入探究空间与数量之间的隐藏关系.因此，教师的教学思路应当与时俱进，改变以理论为主的教学方式，选择组织富有趣味性的探究实验活动，弥补传统数学教学体系的不足之处，鼓励学生在实践过程中应用所学的数学知识.这不仅能营造集思广益的学习环境，也能有效发展学生的直观想象能力.

例如，教师在教学湘教版高一数学必修第二册第4章“立体几何初步”中“直线与平面垂直的判定”这一知识点时，引入了两个富有趣味性的探究实验.实验一，教师展示了一张旗杆在一天中影子变化的不同照片.随着太阳的东升西落，旗杆的影子位置会不断发生变化.教师让学生思考：在太阳移动的过程中，旗杆与其影子形成的角度是否会发生变化？针对这个问题，教师并没有让学生立即作答，而是先前往操场，实地考察国旗旗杆，用量角器测量旗杆与影子的角度大小，在实践和讨论过程中大胆给出答案.实验二：在△ABC的底边BC随机选一点D，沿直线AD将三角形对折，将对折后的三角形立在桌面上，保证底边与桌面重合.此时，分析AD与该桌面是否属于垂直关系.在大多数学生的想象中，折叠后的三角形可以轻易稳定在桌面上.继而会产生一种错觉，认为AD与桌面属于垂直关系.但经过亲手实践、亲眼观察，学生能明显发现AD所在的直线不一定与平面垂直，从而推翻之前的错误结论.由此，通过实践操作的方式，让学生的推理论证过程更为严谨，使其在探究过程中慢慢总结出直线垂直于平面的判定要点，有效培养学生的直观想象核心素养.

七、实施综合评价，加强反思总结

在培养学生直观想象素养的教学过程中，教师不能只重视教学过程，还应当完善教学评价环节，全面评估学生的直观想象发展情况，并做好归纳工作.可采用综合性的评价方式，从多角度入手，帮助学生加强反思总结.具体实施如下：

一方面，教师可为学生准备几道试题，题目内容如下：①已知某学校建设了400米标准跑道，两个弯道为半径为36米的半圆弧，试求直道的长度为多少.该题需要学生能准确计算圆的周长为多少，求出半圆弧长的具体长度，再求解出直道的距离.②在平面直角坐标系中，点A的坐标为（1，0），点B的坐標为（4，0），两点到直线l的距离恰好为1和2，试求直线l有多少条.该题需要学生能联想到圆与直线相切的知识点.同时，通过画图的方式，确定以A和B为圆心的两个圆恰好属于相切的关系，从而找出第三条特殊直线x=2.最后，根据学生解答的具体步骤以及选择的解析方法，教师可以全面评估学生的直观想象素养水平.

另一方面，借助移动设备，将学生的上课情况摄录下来.通过视频回放，教师能认真观察到学生的学习表现，根据学生回答问题的具体情况，评价学生的直观想象能力发展情况.例如，有的学生在回答时不能将数学问题直观化，思维过程有一定的局限性，缺乏数形结合的做题意识.有的学生缺乏良好的空间想象力，不能从三维的角度理解图形的变化特点.针对学生的不足之处，教师在后续的教学中要制订训练计划，为学生发放合适的练习题，或布置有针对性的实践活动，以起到查缺补漏的教学效果.

结 语

综上所述，情境教学、实验教学等多种方式，可以消除传统数学课堂“重理论，轻实践”的弊病，将抽象难懂的几何、函数等知识放置在学生熟知的生活情景或实践活动之中.这样能让学生产生身临其境的学习感受，有效简化数学知识的理解难度，对学生直观想象核心素养的发展也大有裨益.

【参考文献】

[1]曹素玲.高中数学课堂教学中落实直观想象素养培养的设计[J].上海中学数学，2022（9）：39-41.

[2]俞大明.浅谈在高中数学教学中培养学生直观想象素养的策略[J].求知导刊，2022（13）：35-37.

[3]金仕针.高中数学教学中直观想象素养培养的路径探究[J].考试周刊，2022（17）：87-90.