异构多智能体输出调节量化自适应跟踪控制

马梓元，万茹，龚华军，王新华

（南京航空航天大学自动化学院，南京 211106）

0 引言

多智能体系统（Multi-agent system，MAS）概念的提出旨在解决复杂控制系统中多个被控对象同时参与多种控制任务的问题，并且被广泛应用于无人机［1］、航天器［2］和无人船［3］等领域。当前，多智能体系统在理论及工程应用领域都得到极大关注，多智能体系统的研究通常针对复杂条件下一阶、二阶甚至更高阶智能体模型之间的协同控制［4-5］，同时被控对象的自适应能力与更好的编队跟踪能力也成为研究学者重点关注的问题，并在无人飞行器感知及协同编队、复杂航天器协同自适应控制［6］等领域取得了较为瞩目的理论及应用成果。

MAS 通常由智能体的动力学模型集合、通信拓扑和分布式控制器3个基本要素构成。有关于分布式控制器的设计则往往基于通信拓扑下跟踪误差的重新整定。一致性控制问题是MAS 的主要研究分支之一，旨在利用通信网络拓扑实现MAS 内每个智能体向参考指令的一致性跟踪。每个智能体的跟踪控制器需考虑通讯拓扑结构，即认为跟踪控制器输出信号的计算依赖于通信网络拓扑，以及在该网络拓扑下的一致性跟踪误差，具有显著的聚集行为特征。

然而，在多智能体系统一致性跟踪控制问题的研究中，关于部分状态信息丢失的研究较少，尤其在部分通道信息整体丢失时，如何利用降维输出变量构建基于输出调节的一致性跟踪控制器，成为MAS 一致性控制问题中的新难点。当前，关于输出调节问题的研究仍多集中于单一被控对象，如文献［7］在固定翼飞行器的控制律设计中，运用输出调节模型参考自适应方法将飞机的近似开环线性模型配置到稳定的闭环极点上，而文献［8］则进一步讨论了该方法所采用的输出变量信号的最小阶数。文献［9］提出一种基于反步法的输出调节方法，结合状态观测器设计输出调节自适应控制器。上述方法虽然解决了单一被控对象的输出调节问题，但考虑MAS 一致性控制问题中虚拟误差变量引入后的控制器实现，上述方法仍不能直接应用，需要依据通信拓扑进行进一步改进。

同时，在实际控制系统中，尽管MAS 的开环动力学模型中每个智能体的状态都为连续时间状态，但控制器的实际输入受到控制回路中执行机构及硬件电路的影响，往往被视为一类量化的输入信号。有关于量化控制信号的概念最早出现于网络控制系统的研究中，指控制信号在通信中不可避免地被转化为一类或几类量化信号，实际控制输入则由量化信号给出。量化输入信号的引入将降低闭环控制系统性能，因此针对量化输入问题的研究在近年逐渐获得关注，并取得一些理论进展。考虑到系统内部参数的不确定性，部分基于自适应量化控制的方案也逐渐被提出，但大多基于单一动力学系统。比较常见的自适应量化控制方案大多基于单输入单输出系统假设，基于反步法控制架构解决严格反馈系统下的控制问题。文献［10-14］对输出调节及外界扰动抑制问题进行了相应的研究。文献［15-16］采用基于卡尔曼滤波的模型参考鲁棒自适应控制器，通过卡尔曼滤波器对系统状态进行预估的方式，提高控制系统性能。然而，针对MAS 系统的输入量化问题却很少得到研究，其主要原因在于MAS系统在考虑通信拓扑及内部智能体参数耦合后，严格反馈系统假设可能不成立，同时基于反步法的控制结构导致MAS 系统控制效率显著降低。因此在MAS框架下研究输入量化问题也具有较大的难度。

本文提出一种基于一致性理论的输出调节量化自适应跟踪控制算法，用于解决参数不确定条件下MAS系统的编队跟踪问题。并针对无人机-无人船组成的异构多智能体系统模型开展数值仿真，验证本文提出的控制算法的有效性。

1 问题描述

1.1 多智能体系统动力学模型

首先针对由N智能体组成的MAS 中每个智能体进行建模。认为第i个智能体可以描述为Mi输入Mi输出的近似线性时不变系统形式，i=1，2，…，N，MAS系统动力学模型可描述成下述形式：

在本文中，考虑量化输入的MAS 闭环系统的设计将依赖于下式：

式中：A，B，C为未知的系统状态参数矩阵。由式（4）改写得到的输入输出描述为：

式中：Gi(s)为第i个智能体的输入-输出传递函数，G(s)则为MAS系统的输入-输出传递函数矩阵。

引理 1［17］.为便于后续推导，给出如下引理，对于任意M×M的有理严格正实矩阵，即传递函数矩阵Gi(s)，存在下三角多项式矩阵ξm(s)为Gi(s)的左乘正交矩阵，其矩阵形式为：

本文控制器的设计基于如下假设：

假设 1.系统G(s)=C(sI-A)-1B渐近稳定且可观测。由此保证本文MAS 闭环系统可控，且状态信息全可获取。

假设 2.Gi(s)为满秩矩阵且其左乘正交矩阵ξm已知。

1.2 通信网络拓扑描述

本文利用固定有向拓扑进行MAS 通信网络的描述。图论用于描述MAS 系统中智能体之间的通信流向，详见参考文献［17］中的具体解释。将MAS中的有向拓扑图表达为G=(V，E，A)，其中V={vi，i=1，…，N}为拓扑图的节点集合，E⊆V×V为边界集合，A=[ai，j]∈RN×N为拓扑图的邻接权值矩阵，且对于(i，j) ∈E，i≠j，aij=1，否则aij=0。同时，定义L=D-A为G=(V，E，A)的Laplacian 矩阵，其中D=diag(d1，…，dn) (n=1，2，…，N)，di=

定义一个编号为0 的虚拟领航者，让其跟随参考指令输出ym领航者，则可以将有向拓扑图G=(V，E，A)扩展为其中为相应扩展的边界集和邻接权值矩阵。

1.3 控制目标

本文假定各跟随者的输出yi状态维数相同且与ym保持一致，通过设计控制器使得每个跟随者的状态yi(t)一致性趋近ym(t)。

定义第i个智能体的输出跟踪误差为：

若仅对每个独立智能体进行控制，则控制目标为ei(t)有界。为解决MAS 系统的一致性跟踪问题，进一步定义针对第i个智能体的一致性输出跟踪误差矩阵ϵi(t)如下：

上式中，若第j个智能体可获取领航者的状态信息，则di=1，否则di=0。将MAS 跟踪误差与一致跟踪误差表达为：

则ϵ与e有如下关系：

编队跟踪控制的目标为使ϵ有界。运用多变量模型参考自适应（MRAC）方案对MAS 进行输出匹配，即要求被控对象跟踪下述参考模型：

式中：r∈RM为有界的参考输入信号，根据假设2，容易得出Wm(s)是稳定的。

2 编队控制器设计

2.1 标称输出调节编队跟踪控制结构设计

标称控制结构主要用于给出各模型参考已知且不考虑输入量化前提下的控制器输出反馈形式。在模型参数已知的前提下，针对第i个智能体，首先利用系统输出yi=Cixi观测系统状态并基于观测状态设计反馈控制结构。给出基于观测状态设计的标称反馈控制律：

由于需确保设计的控制器能够使闭环系统配置到参考模型上，给出下述标称控制器参数和匹配条件：

由此，全状态观测器表达为：

求解式（16），容易得到：

式中：εi0(t)代表由初值引起的误差影响，通常可被忽略，Λi(s)=det(sI-+)。将标称控制器的状态反馈部分表示为：

2.2 输出调节编队跟踪自适应量化控制器设计

在本文探讨的控制问题中，状态空间参数矩阵Ai，Bi，Ci均未知，且控制输入引入了额外的延迟量化信号。在上述条件下，考虑基于自适应律估计各反馈增益。然而，对三个状态矩阵Ai，Bi，Ci的直接自适应估计存在较为复杂的耦合，因此考虑在频域内对高频增益矩阵Kpi进行LDS分解，实现自适应估计变量的解耦和参数化。给出如下假设：

假设3.高频矩阵Kpi的所有顺序主子式Δi，i=1，2，…，M都是非零的，并且它们的符号已知。这样的Kpi具有非唯一的LDS矩阵分解

考虑到输出量化问题，对第i个智能体，给定一个虚拟输入变量vi，引入一个稳定的多项式f(s)，其次数等于左交互矩阵ξm(s)的最大次数。定义滤波器h(s)=1/f(s)，将自适应编队跟踪控制器表述为：

式中：η＞0 为待整定系数，m由（32）给出。针对每个智能体的输出跟踪误差，代入控制器（21），将跟踪误差改写为：

利用高频增益矩阵Kpi的LDS 分解对每个智能体跟踪误差中的自适应变量实现参数化求解，同时将式（22）改写为：

进一步将该方程进行参数化，利用滤波器h(s)对估计误差方程进行修正，将等式表示为：

则等式进一步改写为：

为实现控制对象向参考模型的跟踪，除了要求跟踪误差收敛外，还需实现模型的输出匹配，即要求高频增益矩阵及控制器参数收敛到标称值。基于每个智能体的输出跟踪误差首先构建第i个智能体的参数估计误差方程：

2.3 控制器稳定性分析

对本文提出的基于自适应律设计的参数估计有界性进行分析。定义Lyapunov函数如下：

考虑量化输入信号q(u)，根据文献［11］，认为：

根据式（36），式（35）中部分项可改写为：

根据Young不等式［16］，有：

式中：kd＞0为待定系数。从而将式（38）整理为：

回顾控制器（21），根据文献［12］，存在下述关系：

结合L+D＞0，S=ST＞0，则有：

式（40）可进一步整理为：

根据式（43），将式（35）最终化简为：

3 仿真验证

为验证本文提出的编队控制方法可行性和有效性，在MATLAB 环境下开展p艘无人船与q架无人机组成的异构MAS系统在xoy二维平面内的编队数值仿真，p≥2，q≥2，p+q=N。对q架无人机的飞行编队，给出第i架无人机的运动学方程如下：

式中：xi，yi代表第i架无人机在x，y方向的位置，vi为第i架无人机速度，ψi为第i架无人机的航向角，ωi为第i架无人机的航向角速度。无人机的动力学方程采用简化的近似线性状态方程，第i架无人机的动力学方程如下：

式中：Ai，Bi，Ci为第i架无人机的状态矩阵，mi=[vi，ωi]T，模型控制 输入ui=[δTi，δri]T为油门开度与差动副翼舵偏角。无人机动力学模型表示成式（4）的形式，则第i架无人机状态变量表示为=[xi，yi，ψi，vi，ωi]T，模型输出为=[fi，li]T，其中fi，li分别代表无人机前向与侧向位移，其表达为：

对p艘无人船组成的航行编队，第j艘无人船的运动学方程如下：

式中：xj，yj为第j艘无人船位置，ψj为第j艘无人船偏航角，uj，vj，rj分别为无人船在船体坐标系下的前向速度、侧向速度及偏航角速度，j=q+1，…，N。无人船的动力学模型如下：

式中：mu，mv，mr为船体惯性参数，控制输入uj=[τuj，τrj]T，非线性项fw(w)，fv(v)，fr(r)定义为

无人机动力学模型参数由文献［18］给出，无人船动力学模型参数由文献［19］给出。无人机数量为2架，无人船数量为2艘。输入量化参数δ=0.8，umin=0.02。将参考模型选取为：

参考输入指令选取为：

仿真结果如图1～2所示。仿真结果表明，在无人船控制通道采取量化输入形式时，各闭环信号仍能保证对时变参考输出信号的一致跟踪，从而验证了本文所提出的编队控制算法的有效性。

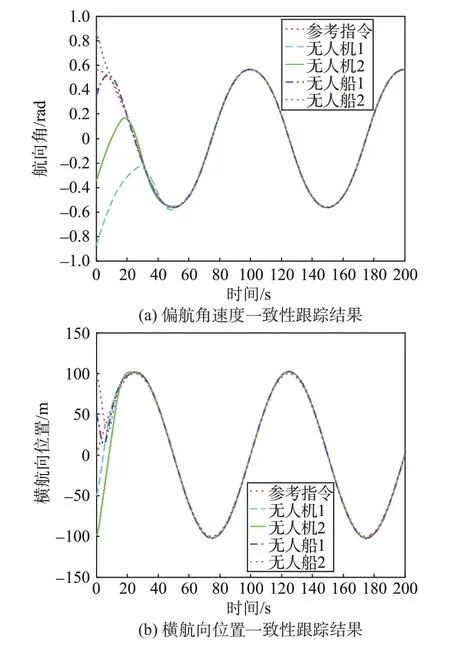
图1 各输出响应一致性跟踪结果Fig.1 Consensus tracking result of each response

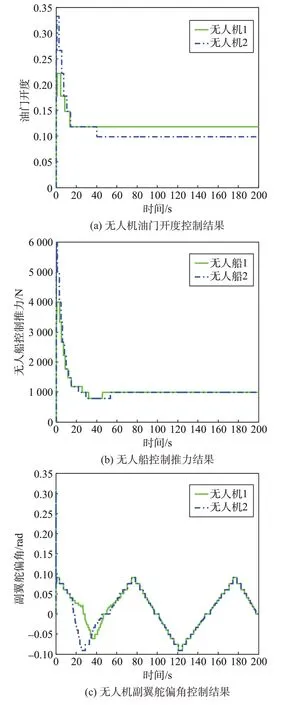
图2 量化输入结果Fig.2 Results of quantized input

4 结论

本文提出了一种基于输出调节量化自适应一致性的编队跟踪算法，用于解决硬件在环假设下控制输入量化后的异构多智能体一致性跟踪控制问题。基于输出调节思想，认为系统内部分状态整体丢失或不能获取，利用仅有的降维输出实现各闭环信号的一致性有界跟踪。通过理论分析及数值仿真分别验证了所提出方法的有效性。