一种组合动力飞行器模态转换过程轨迹优化与控制方案

刘凯，张永亮，聂聆聪

（1.大连理工大学力学与航空航天学院，大连 116024；2.北京动力机械研究所，北京 100074）

0 引言

为了适应低成本天地往返运载需求，可重复使用的自主水平起降宽速域飞行器成为各国研究热点。因其宽速域特点，传统涡扇发动机不能满足高马赫数下的推力需求，冲压发动机无法在低马赫数下稳定工作。涡轮基组合循环（Turbine-based combine cycle，TBCC）发动机方案通过组合涡扇与冲压动力系统，兼顾飞行器宽速域内推进性能需求，成为设计速域在Ma0～7内的宽速域飞行器理想动力方案［1-3］。宽速域飞行器起飞爬升加速过程中，亚声速与低马赫状态涡扇单独工作，当飞行器临近涡扇发动机工作包线边界时，涡扇/冲压共同工作（以下称模态转换），最后达到冲压单独工作状态。其中模态转换阶段需要调整进气道分流板与尾喷管，将一部分进气道压缩流从低速涡扇流道分流到高速冲压流道并产生推力［4-5］。此时冲压流道内部燃烧不稳定，对来流状态与燃油当量比的要求和限制十分严格，极易发生进气道不起动［5］；此时宽速域飞行器的飞行速度接近涡扇系统的设计极限，又尚未达到冲压系统的有效工作区间，导致推进系统提供的总推力不足，形成“推力陷阱”现象，给飞行控制带来新的挑战。因此，对涡轮基组合循环发动机方案模态转换过程的相关研究有重要的工程实践意义。

近年来，一些学者对TBCC模态转换过程与推力陷阱问题进行了研究。文献［7］介绍了包括变循环方案、预冷方案和火箭助力方案在内的3 种提升涡扇发动机工作上限的发动机设计方法。文献［8-9］分别提出了多催化剂接力催化的自由基接力燃烧（FRRC）策略来大幅降低煤油点火温度和优化进气道回流区附面层抽吸设计，从而使冲压发动机实现低马赫数起动。文献［10］采用动网技术分析攻角对外二元并联TBCC 模态转换期间进气道出口气流状态的影响。文献［11］以进气道流量分配比例变化为条件，分析了模态转换段TBCC 性能参数的变化规律，阐述了发动机性能衰减的主要原因。

目前国内外学者关于模态转换与推力陷阱的研究集中于产生机理分析，提升涡扇发动机工作上界，降低冲压发动机工作下界以及飞行状态对发动机性能影响分析等方面，鲜有从轨迹优化与飞行/推进一体化控制的角度给出模态转换阶段的解决方案。宽速域飞行器采用飞推一体化构型设计，单独对推进系统或飞行状态进行解耦分析设计无法系统性地克服推力陷阱。

因此，本文针对一型TBCC 宽速域飞行器进行飞行动力学建模、定量分析模态转换过程的推进系统能力与推力需求，通过轨迹设计克服模态转换阶段的推力陷阱，采用轨迹线性化制导方法实现飞行/推进一体化控制，为解决宽速域飞行器推力陷阱问题提供一条新的技术途径。

1 宽速域飞行器动力学建模

1.1 宽速域飞行器质点动力学模型

在飞行器航迹坐标系下，依据经典牛顿定律，飞行器的质心运动可以用如式（1）的矢量方程形式表述：

式中，m是飞行器质量，V为飞行速度，Ω是转动角速度，F是飞行器合外力矢量，T是推力矢量。忽略地球自转影响，根据飞行器航迹坐标系与地面坐标系之间的转换关系，整理可得飞行器三变量质心运动的动力学方程如式（2）所示：

式中：θ，ψ，h分别表示飞行器航迹倾角、飞行器航迹偏角、飞行高度；D，L为阻力、升力；α，γ为攻角、倾侧角；δz，δe，δr分别为升降舵偏角、副翼偏角、方向舵偏角。

1.2 模态转换阶段轨迹策略分析

本文基于激波理论构建二维进气道模型，得到进气道出口的流场参数。采用T-mats 工具包建立涡扇发动机模型，依据质量守恒、动量守恒和能量守恒，建立准一维冲压发动机模型。采用面元法分析宽速域飞行器气动特性［12-13］。

对于经过优化设计后的TBCC 模态转换过程，转换速域能够降低至Ma2.1～2.6。此时涡扇发动机效能不能满足推力需求。另一方面，飞行速度低导致冲压发动机进气道内无法形成足够强的激波系从而对自由流进行有效压缩，抗反压能力很弱。燃油当量比受限于进气道不起动保护约束和贫油熄火约束之间，导致其值和调节范围都很小。冲压发动机也不能提供足够的推力满足飞行器推力需求。综上所述，模态转换阶段飞行器的核心需求是加速，使飞行马赫数达到冲压发动机的正常工作区间，完成模态转换。

首先对模态转换区间内的TBCC 性能与宽速域飞行器推力需求进行分析，对比飞行器平飞加速最小推力需求与TBCC 最大推力能力。宽速域飞行器在设定飞行状态的配平攻角如图1所示。

图1 配平攻角Fig.1 The trim angle of attack

在得到宽速域飞行器配平攻角的基础上，可以求解得到飞行器在设定飞行状态下的阻力。结合涡扇与冲压发动机性能，可以对比阻力与总推进能力。图1为考虑宽速域飞行器飞推耦合效应的气动特性情况下，配平攻角与飞行状态之间的关系，图2为配平攻角下推力需求与推进系统能够提供最大推力的对比。

图2 推力裕度与飞行状态关系Fig.2 Relationship between thrust margin and flight state

可以看出，宽速域飞行器组合动力发动机在Ma2.25～2.55 速域内，即冲压发动机尚未达到有效工作区间的阶段，出现最大推力不满足平飞加速所需最小推力的推力陷阱现象。在此阶段，需要采用特殊轨迹设计，使宽速域飞行器跨越推力陷阱，恢复机动能力，如图3所示。

图3 模态转换阶段的轨迹优化策略Fig.3 Trajectory optimization strategy in mode transition

具体轨迹策略是把帮助宽速域飞行器完成模态转换的轨迹设计分为2 个阶段：第1 阶段是爬升预备阶段，此阶段需要宽速域飞行器利用涡扇发动机达到足够的高度和速度，给模态转换和可能的俯冲加速做动能和势能储备；第2 阶段为模态转换阶段，此阶段涡扇发动机和冲压发动机共同工作，利用优化后的飞行轨迹进行进一步加速，达到冲压发动机的正常工作速域。

在轨迹规划上，第1 阶段设定飞行目标是使飞行器达到涡扇发动机的极限高度和冲压启动速度；第2阶段的主要目标是使飞行器达到冲压发动机正常工作的速度要求，而相应地放松对飞行器的高度限制。

2 宽速域飞行器飞推一体化控制器设计

2.1 基于自适应高斯伪谱法的模态转换轨迹优化

Gauss 伪谱法［14-15］由于在计算效率上表现出显著的优势广泛应用于求解最优控制问题，同时在航空航天领域常用于轨迹优化。该方法通过对控制量和状态量进行离散，直接进行寻优解算，从而完成非线性规划任务［16］。

考虑一般形式的非线性系统动力学方程为：

式中：状态变量x(t) ∈Rn，控制变量u(t) ∈Rm，时间t∈[t0，tf]。

若最优控制的时间范围是[t0，tf]，而Gauss 伪谱法时间范围是[ -1，1]，则对时间t进行变换可以表示为：

Gauss 伪谱法经过离散处理的点为K阶Legendre-Gauss点，等价于K阶Legendre 项式的根k={，…，，}。增加额外点=-1，作为第K+1个插值点，然后以K+1 个Lagrange 插值多项式Li()(i=0，1，…，K)为基函数，进行状态变量的近似：

式中：wk=为Gauss 权重系数，为Legendre-Gauss点。

同样地，用Lagrange 插值多项式为基函数来近似控制变量，其中U()，(k=1，2，…，K)为离散点上的控制变量(i=1，2，…，K)为Legendre-Gauss点。

对式（6）求导得到状态变量的导数，可以将动力学方程约束变为代数约束，再反代入动力学方程，则得到状态变量在配点处应受的代数方程约束：

边界条件约束满足：

过程约束满足：

用Gauss 积分近似最优控制问题中性能指标函数的积分项，可以得到性能指标函数：

此时的最优控制问题已经被转换为：使得经过离散化后的状态变量Xi、控制变量Uk以及终端时刻tf，在满足动力学方程约束的前提下，求解J函数最小，即式（10）最小。

2.2 模态转换阶段轨迹策略对比仿真

第1 阶段宽速域飞行器以爬升为目标，设定第1 阶段的状态量和控制量约束如表1所示。

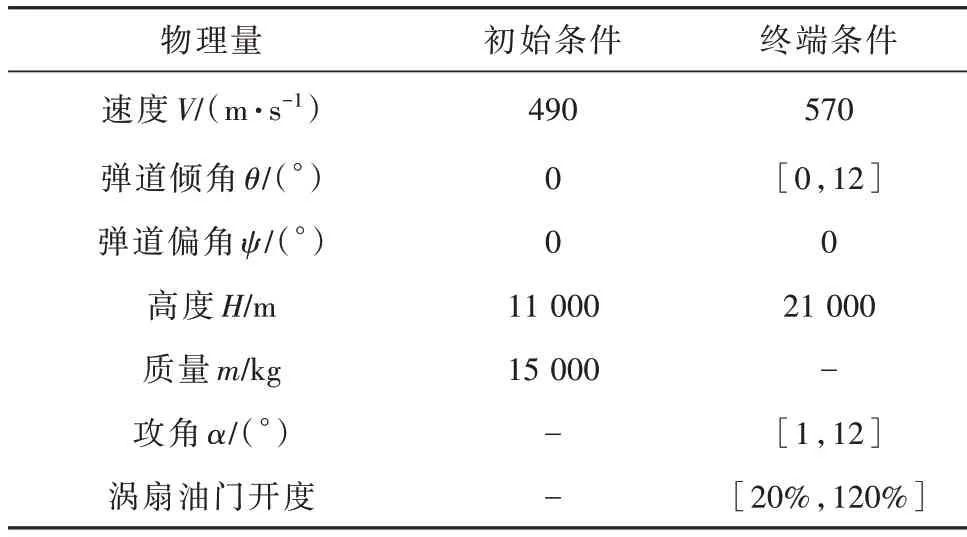
表1 爬升段状态量及控制量约束Table 1 State quantity and control quantity constraints in climbing stage

采用高斯伪谱法优化且经过积分验证的优化爬升轨迹如图4所示。

图4 涡扇爬升段优化轨迹Fig.4 Optimized trajectory of the climbing section

由图4 优化爬升轨迹可知：在最终高度差小于200 m，最终速度差小于4 m/s 的情况下对比，最短时间路径对比最少油耗路径少用时间39.4 s，多消耗油料66.4 kg。将该阶段的末端飞行状态作为第2 阶段（模态转换段）的初始状态，进行第2阶段的轨迹优化。

由表2 可知模态转换阶段马赫数较小，冲压发动机燃烧不稳定，过大的燃油当量比容易引起进气道不起动和点火困难［17-18］。因此将燃油当量比限制为常值0.35。采用高斯伪谱法优化且经过积分验证的模态转换阶段轨迹如图5所示。

表2 模态转换段状态量及控制量约束Table 2 State quantity and control quantity constraints of mode transition

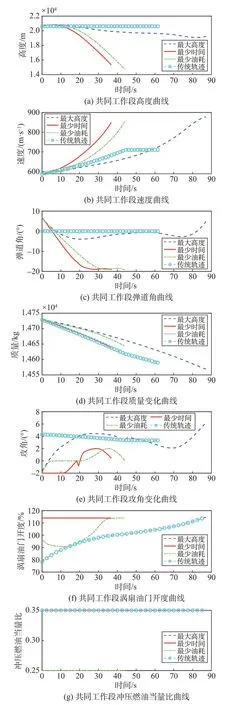
图5 宽速域飞行器共同工作加速段轨迹优化Fig.5 Velocity and thrust response curves

由图5 可以看到，传统轨迹在达到710 m/s时，遭遇推力陷阱，推力和推力需求此时达到平衡，无法加速。优化轨迹均可以克服推力陷阱，达到目标速度。最大高度轨迹耗时61.5 s，下降高度1.37 km；最少时间轨迹耗时36.8 s，下降高度5.3 km，比最大高度轨迹少消耗燃油60 kg。最小油耗轨迹比最少时间轨迹多耗时7.2 s；少消耗燃油5.4 kg；高度少下降615.1 m。

3 宽速域飞行器轨迹线性化控制策略

本节基于前文所建的质点动力学模型，对宽速域飞行器进行轨迹线性化控制设计。为完成宽速域飞行器制导环设计，以速度、高度和横向位置作为状态，同时引入速度积分项，高度微分项和航向位置微分项将模型扩维，如下式所示：

需要注意的是，阻力和升力项应为各个状态微分的输入量，状态量以非线性气动模型计算得到，推力由组合动力系统性能模型确定。沿飞行轨迹采用线性化方式拟合得到以上参数。通过轨迹线性化方法，得到差分形式的轨迹线性化方程，进而将状态空间表达式转换成矩阵形式，把引入的扩维状态设计成状态空间表达式后，可以做出如式（12）～（13）的变量命名：

式中：s为飞行器在地面坐标系下的飞行距离；z为飞行器在地面坐标系侧向，即z轴方向的飞行距离。整理为误差状态方程形式有：

误差状态方程中的输入项应为u(t)=[α，γ，φk]T；其中φk指涡扇油门。

3.1 宽速域飞行器轨迹线性化控制算法

轨迹线性化控制（Trajectory linearization control，TLC）的设计思想是：首先利用开环系统被控对象的伪动态逆，将轨迹跟踪问题转化为一个时变非线性系统的跟踪误差调节问题，然后设计闭环的状态反馈调节律使得整个系统获得满意的控制性能。在将控制问题转化为跟踪问题后，可以实现将多个被控变量同时稳定到目标值；并且由于TLC 控制方法可以调整闭环系统的极点位置，所以能够保证多变量控制效果［19］。

针对得到的线性时变误差系统，采用如下形式的时变控制器：

式中：uc(t)是轨迹优化结果为针对误差产生的控制增量：

将期望闭环矩阵设置为如下形式：

对式（24）进行拉普拉斯变换，并且基于扩维动力学方程，即式（11）可知，6 维状态空间可以分为3 个子空间，每个子空间可以对应一个线性时变二阶系统，进一步描述为特征方程形式，即为：

这里ς1(t)，ς2(t)，ς3(t)和ω1(t)，ω2(t)，ω3(t)分别表示阻尼比和自然频率，可以基于期望的系统动态性能即上升时间和超调量来确定，从而使解算得到的控制器参数能够满足希望的动态性能要求。

按照目前欠阻尼二阶线性系统对于阶跃响应的上升时间tr和超调量σ估算公式：

由于3 个子系统均为二阶时变系统；所以引入PD谱定义：

PD 谱用ρ1(t)，ρ2(t)来描述时变系统的特征根，即系统方程的解可描述为：

与二阶系统方程系数的关系满足

稳定性分析判据：二阶线性时变系统渐近稳定的充分必要条件是其PD 谱满足二阶系统的解均具有负实部，即：

3.2 宽速域飞行器轨迹线性化控制仿真

本次仿真的标称轨迹为最小时间优化轨迹；在仿真中，进行了升力、阻力系数±10%拉偏情况，仿真结果如图6 所示：TLC 控制算法仿真误差如表3所示。

表3 TLC控制算法仿真误差Table 3 Simulation error of TLC control algorithm

图6 TLC控制算法仿真结果Fig.6 Simulation results of TLC control algorithm

由图6 可以得到：在对升力或阻力施加了±10%拉偏的情况下，飞行器最终高度误差不大于3.620 3 m，百分比误差不大于0.023 4%；速度误差不大于3.723 m/s，百分比误差不大于0.043 8%。飞行器攻角在19 s 时出现尖峰（指令信号波动现象），这是模态转换过程中推力陷阱通过飞推耦合效应在飞行控制中的体现。基于轨迹线性化设计的时变控制器控制精度高，能够实现高机动任务要求。

4 结论

针对TBCC 宽速域飞行器模态转换过程中容易出现的推力陷阱问题，本文验证了大飞行包线内推力陷阱现象广泛存在，提出了模态转换期间以势能换动能的飞行轨迹策略，支撑解决组合动力模态转换过程中的推力陷阱问题。完成了爬升段和模态转换阶段的轨迹优化设计，给出了基于轨迹线性化制导的飞推耦合一体化控制策略，以模态转换阶段的最大高度轨迹为标称轨迹给出的仿真，说明了该方法的有效性和优势。