高超声速飞行器时间协同预测校正鲁棒制导

魏昀鹏，都延丽，王文凯，刘燕斌

（南京航空航天大学航天学院，南京 211106）

0 引言

高超声速再入飞行器凭借其飞行速度快、打击距离远、机动性强等优点，将成为支撑全球快速打击作战的重要武器。多高超声速飞行器协同作战利用成员之间信息共享、相互配合、职能互补的群体协作，不仅能最大限度地发挥其作为先进远程高速打击武器的优势，还能显著提高突防能力，高效完成侦察、突防、打击等战场任务，提升高超声速再入飞行器体系化作战能力［1］。作为支撑多高超声速再入飞行器协同作战的关键技术，协同再入制导方法引起了广泛的关注。

对高超声速飞行器而言，滑翔段的飞行时间占据了再入过程的绝大部分，远大于末制导段，且末制导段协同任务也十分依赖滑翔段提供良好的初始条件［2］。但由于滑翔段飞行器间距大、“黑障”影响强，难以形成切实的飞行器间数据链，导致基于信息交流的理论难以应用于滑翔段协同制导。一般采取不使用飞行器间通信的绝对时间协同制导［3］。而如何通过预测飞行时间进而实现对其精准控制成为了高超声速飞行器绝对时间协同制导的关键问题。文献［4］采用标称轨迹制导结合多维度制导思想对再入飞行器的时间协同展开研究，分别从纵、横平面展开设计，纵平面保证制导精度，横平面设计对称航向误差飞行保证飞行时间的协同；文献［5］通过结合多维度制导，采用BP神经网络在纵向制导期间在线预测剩余飞行时间，横向修改航向误差走廊的宽度以满足飞行时间约束；文献［6］基于预测校正制导，结合多阶段制导，将再入滑翔段制导分为两个阶段：第1 阶段通过调整倾侧角实现攻击角度协同，第2 阶段通过对攻角优化实现攻击时间协同；文献［7］基于参考轨迹协同制导方法提出采用公共轨迹长度作为协调变量的思路，通过实际轨迹长度与总飞行时间的对应关系，设计了一种双层协同框架，将终端时间的一致性问题转化为到达截止时间的状态收敛问题，设计对称航向误差飞行保证飞行时间的协同。

以上研究主要讨论了标称环境下的协同制导方法，然而，上述方法难以直接应用于存在参数不确定性的实际协同制导问题中。在高超声速飞行器滑翔段协同制导过程中，飞行高度和速度变化剧烈，制导系统会不可避免地受到各种扰动的影响，从而对协同飞行时间和制导精度产生影响。因此，如何改善高超声速飞行器协同制导律的鲁棒性能成为目前协同制导律研究的一个重要问题。

采用具有更强鲁棒性的制导方法是一种处理外部扰动和参数不确定性的方法。目前，大量协同制导方法是基于标准轨迹制导方法展开的，而标准轨迹制导过程中通常采用滑模控制［8］、鲁棒控制［9］、自适应控制［10］等先进控制方法提高系统的鲁棒性。相较于标准轨迹制导，预测校正制导方法不依赖参考轨迹，且对初值不敏感，在鲁棒制导领域有着较强的优势［11］。文献［12］基于预测校正制导对绝对时间协同展开研究，根据飞行时间约束生成飞行剖面，并在横平面通过跟踪Bézier 曲线表示的横向轨迹控制倾侧角翻转时间，实现协同制导的同时有效抵抗了参数不确定性的影响；文献［13］基于滑翔段剩余飞行时间和剩余飞行距离估计解析表达式，采用预测校正方法将纵向升阻比作为设计量，实现了存在参数不确定性条件下的时间约束再入制导。

另一方面，通过飞行器的量测数据，实时地辨识飞行中的不确定参数，对原有制导控制系统进行补偿，也是一种有效提高系统鲁棒性的方法［14］。文献［15］以卡尔曼滤波理论作为基础，推导了再入飞行器气动参数辨识的数学模型，根据获得的带有测量误差的惯导信息，对气动参数进行估计；进一步地，文献［16］对大气密度和飞行器气动参数扰动引起的预测模型不确定性进行在线参数估计，将估计后的参数补偿至基于预测-校正的制导算法中，利用再入过程中横程与剩余航程的近似线性关系，设计边界约束动态变化的横程走廊以控制倾侧角翻转。

基于以上分析，采用鲁棒性较强的预测校正制导方法结合参数辨识方法是实现协同鲁棒制导任务的一种可行方案。因此，本文针对不确定环境下的高超声速飞行器滑翔段协同制导问题，提出了一种时间协同的预测校正鲁棒制导方法。

1 问题描述

1.1 多高超声速飞行器运动模型

对于多高超声速飞行器协同制导任务的第i个成员，通过引入ei作为能量变量，将飞行器运动方程转化为关于ei的方程，其中ei可表示为：

式中：Ri表示飞行器的无量纲地心距；vi表示飞行器的无量纲速度。则以能量ei为自变量的无量纲3 自由度运动方程为［17］：

式中：θi与ϕi分别为飞行器的经度和纬度；γi为飞行器的航迹倾角；ψi表示航迹方位角；σi是倾侧角；Ω为地球无量纲自转角速率；Di和Li分别代表飞行器无量纲阻力和升力，可由下式计算得到［17］：

式中：Si为机翼参考面积；CD，i为阻力系数；CL，i为升力系数；ρ表示当地大气密度；mi表示飞行器质量；g0表示海平面重力加速度。

1.2 路径约束

为保证飞行器安全完成任务，再入过程需要严格满足最大允许过载、动压和热流密度约束的要求，约束条件如下［17］：

1.3 协同任务终端约束

对于滑翔段协同再入任务，飞行器间距大、“黑障”影响强，难以有效地形成飞行器间数据链。因此，在协同制导过程中采用绝对时间协同制导，即在滑翔段协同制导任务开始之前，对所有飞行器设定相同且不再变化的协同飞行时间tf，以tf为准使所有飞行器同时抵达目标。对于多高超声速飞行器不同起始点同时开始滑翔、同一时间到达同一目标的协同制导任务，为了满足所有飞行器飞行性能的需求，需要根据各飞行器起点到目标点的滑翔最长时间tmax，i和最短滑翔时间tmin，i来确定协同飞行时间tf，以使得多飞行器同时到达目标点。tf依据下式得出：

为实现任务需求，需要满足的终端约束如下：

式中：tf，i表示第i架飞行器的总飞行时间；ef为目标能量；θf和ϕf分别表示目标点的经度和纬度。

2 时间协同预测校正制导方法

2.1 时间协同制导方法的流程

为了扩大飞行器飞行时间的调节范围，本文同时在横向和纵向制导过程中对飞行时间进行调节。在横向制导过程中，设计了一个随飞行器待飞航程变化的动态航向角误差走廊，借助预测校正制导的思想，利用预测的飞行时间对航向角误差走廊进行修正，通过调整倾侧角翻转过程实现对飞行时间的调节。在纵向制导设计中，将剩余飞行时间的误差项引入传统预测校正制导的预测过程，通过设计加权函数将此误差项连同剩余航程误差共同组成新的归一化误差项，然后对新误差项进行校正，在保证制导精度的前提下实现对各飞行器飞行时间的动态调节，以满足同时到达预定目标的协同制导任务要求。时间协同制导方法流程结构如图1所示。

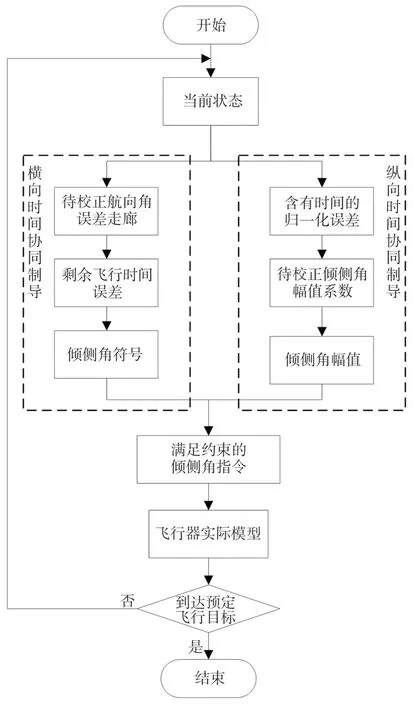
图1 时间协同预测校正制导流程Fig.1 Process of time cooperative predictor-corrector guidance

2.2 动态航向角误差走廊的横向协同制导

传统横向制导过程的目的是将飞行器以较小的航向角误差导引到航向校准柱面内，当航向角误差超过走廊边界时，飞行器以最大的翻转速率执行一次倾侧角翻转机动［18］。定义航向角误差为飞行器当前位置的目标视线方位角与当前水平面内速度方向的夹角：

式中：ψLOS，i表示飞行器当前位置与目标位置之间的视线方位角，计算公式为：

在滑翔段协同制导过程的前中期，通过横向制导调整倾侧角翻转策略实现对飞行距离的控制，从而改变再入飞行时间；而在滑翔段末段，为了避免误差走廊的调整导致倾侧角频繁翻转，设计固定的误差走廊实现对倾侧角符号的控制。

因此，本文提出利用分段函数设计一个如图2所示的飞行器动态航向角误差走廊Δψside，i(si)，具体形式为：

图2 动态航向角误差走廊Fig.2 Dynamic heading angle error corridor

式中：Ki为走廊宽度系数；Δψs1和Δψs2分别为sψ1和sψ2边界情况下的航向角误差走廊宽度。

通过调整误差走廊的宽度系数，可以实现对倾侧角翻转频率的调整，进而影响飞行器的飞行时间。因此，借助预测校正制导的思想，将剩余飞行时间误差看作为走廊宽度系数的函数，即：

根据式（1）和式（2），若不考虑地球自转项的影响，则ei关于无量纲时间的导数为：

则剩余飞行时间ttogo，i关于能量的导数为：

积分可得剩余飞行时间：

式中：e0，i表示飞行器当前能量；ef，i表示飞行器末端能量。则剩余飞行时间误差为：

通过对剩余飞行时间误差进行预测，利用式（15）的迭代法调整走廊的边界宽度系数Ki修正航向角误差走廊，从而实现对飞行时间的控制。

式中：下标i表示第i个飞行器；Kj，i表示走廊宽度系数的第j次迭代；Kj+1，i表示第j+1 次迭代；Kj-1，i表示第j-1次迭代。

2.3 基于误差权值函数的预测校正纵向协同制导

为满足再入初始状态的热保护需求、再入终端阶段的能量效率需求以及航程要求，再入过程中选择标称迎角-速度剖面如下［5］：

式中：αmax和αmin分别为迎角剖面的最大和最小值；vup和vdown分别为切换速度的上下限。

传统预测校正制导方法在纵向制导过程中通过对飞行器待飞航程进行预测，迭代更新倾侧角幅值，实现对待飞航程的校正，但对于多飞行器协同任务，无法实现对飞行时间的控制［19］。通过对传统预测校正制导律进行改进，提出了一个随协同飞行任务进程变化的权值函数ξ(si，ti)，将剩余飞行时间误差引入预测校正过程，采用新的误差项δi代替传统预测校正制导的待飞航程误差：

式中：si表示各飞行器的当前待飞航程；sξ为设计的分段系数，通过对纵向制导过程分段，在协同飞行任务过程中逐步提高协同飞行时间的权重，保证时间协同的同时，避免降低纵向制导精度；ti表示飞行器的当前无量纲飞行时间；sf为目标待飞航程，通常为0；s0，i表示各飞行器初始待飞航程；Δstogo，i为待飞航程误差，具体表达式为：

式中：stogo，i表示预测得到的到达终端待飞航程，通过对飞行器剩余飞行过程积分得到［14］：

在预测校正迭代更新倾侧角幅值的过程中，为了避免线性倾侧角模型在制导周期较长时倾侧角指令不连续的情况，针对指定能量处的倾侧角幅值，本文采用与文献［14］相同的二次函数模型，利用迭代法寻找归一化误差的零点。

注1.在纵向制导预测校正的迭代求解过程中，本文与文献［14］的不同之处在于用本节设计的包含时间项的误差函数代替了待飞航程误差进行计算。

3 考虑存在参数不确定性的协同鲁棒制导

3.1 改进无迹卡尔曼滤波不确定参数估计

针对高超声速飞行器协同制导中的气动参数不确定问题，首先定义再入飞行器气动参数不确定模型为：

式中：CDf，i和CLf，i分别为实际飞行任务中的阻力系数和升力系数；CD0，i和CL0，i分别为标准阻力系数和升力系数；CDd，i和CLd，i分别是阻力和升力系数的不确定参数。将该不确定参数视为标准参数的“机动”，采用一阶高斯马尔科夫过程进行描述，其具体形式为［15］：

式中：λD，i和λL，i分别为不确定参数的机动系数；ωCD、ωCL、ωλD和ωλL均为高斯白噪声序列。

将不确定参数引入到飞行器的状态变量中，则气动参数不确定条件下的系统可表示为：

式中：xi∈Rn为增广后的状态变量；yi∈Rm为量测向量；ω∈Rn和υ∈Rm分别为状态噪声和量测噪声，均服从高斯分布；过程噪声ω的非零均值为q，协方差为Q；量测噪声υ的非零均值为r，协方差为R。其中，xi和yi的具体形式为：

式中：nx，i表示法向过载；ny，i表示轴向过载。因此，式（23）中除噪声的状态微分方程由式（2）和式（22）联立构成，等号右边的9 项即构成了状态函数f(xi)的表达式。式（23）中的量测方程表达式为：

式中：Lf，i和Df，i分别为飞行任务中实际的升力和阻力，可由式（3）结合式（21）计算得到；υx，i和υy，i分别为法向量测噪声和轴向量测噪声。因此，式（23）中量测函数h(xi)的表达式可由式（24）对应得到。

无迹卡尔曼滤波可以有效应用于非线性系统的参数估计过程中。结合飞行器协同制导任务，根据式（23）所描述的系统方程，结合文献［20］给出的无迹卡尔曼滤波算法的一般流程，可以利用无迹卡尔曼滤波算法对未知状态参数进行估计，得到状态量的估计值即：

而在标准无迹卡尔曼滤波算法的sigma 点计算过程中，核心是利用协方差矩阵的平方根进行无迹变换。但由于协同飞行任务过程中，可能有未知扰动和计算误差累计使协方差矩阵出现非正定情况，导致无法计算。为了提高算法的稳定性，本算法利用式（25）对协方差矩阵Pk|k进行奇异值分解，改进无迹变换过程，从而保证算法迭代的连续性。

式中：k表示第k次迭代，Uk|k∈Rn×n，Sk|k∈Rn×n，Vk|k∈Rn×n且Sk|k为非负定的对角矩阵。

则状态变量无迹变换的sigma点集为：

式中：(j)表示点集中列向量的编号；n是状态数量；λ为缩放系数，形式如下：

式中：参数a通常取1，κ通常取0。

除了无迹变换过程外，过程噪声协方差和测量噪声协方差的偏差会降低卡尔曼滤波算法的性能或者导致估计过程不收敛。通过对过程噪声和量测噪声进行更新，可以提高算法精度来保证其稳定性。

根据文献［21］，基于Sage-Huse 算法的极大后验估计更新得到过程噪声和量测噪声的估计为：

式（28）实际上是对所有数据进行平均加权估计，但由于越接近当前状态的估计对算法性能影响越大，对于不断变化的状态噪声估计，应该更重视新的数据。因此，结合协同飞行任务，提出一种借助记忆渐消滤波［22］思想的、自适应更新过程噪声和量测噪声的方法，即：

式中：βk为记忆衰减加权因子，其具体形式如下：

式中：b为遗忘因子，一般取0.9，tk表示算法当前迭代时的无量纲飞行时间。

注2.本节设计了改进的无迹卡尔曼滤波算法对于不确定参数进行估计，该算法将应用于第2 节中对于预测过程飞行器模型的修正和3.2节对于制导系统的补偿之中。

3.2 航向角误差走廊补偿和迎角补偿的鲁棒制导

在上一节中提出了改进无迹卡尔曼滤波算法对飞行过程中气动参数的不确定进行了估计。利用气动参数不确定的估计量，可以对预测校正制导中预测过程的模型进行修正，进而提高系统的鲁棒性。但由于飞行器升阻比的变化，飞行器的纵向和横向飞行性能也随之变化［23］。如果按照原有的纵向和横向制导逻辑，可能会影响飞行器的飞行时间以及末端落点精度，导致协同再入任务的失败。为此，本文引入剩余能量eres，i，具体形式如下：

式中：ef表示飞行任务的末端能量。

图3 为剩余飞行时间和剩余能量的关系，图中剩余能量由无量纲化的高度、速度计算得到，也为无量纲变量。图中可以看出，当升阻比增大时，飞行器的能量耗散速度减慢，飞行器可能无法在协同飞行时间之内完成飞行任务。当升阻比减小时，飞行器的能量耗散速度加快，会使飞行器在协同飞行时间前耗尽能量，导致提前到达目标点。因此，可以通过在标称剖面基础上引入自适应的调整策略，补偿升阻比变化带来的影响。

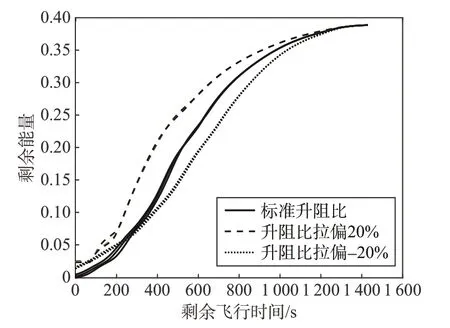
图3 剩余飞行时间-剩余能量对比Fig.3 Remaining flight time versus remaining energy

在横向制导过程中，升阻比变化会影响航向角误差变化速率，进而影响倾侧角翻转情况［23］。将第2.2节中的式（7）对时间求导可得：

根据文献［23］，通常滑翔段飞行过程中航迹角较小，可以近似为0，若忽略地球自转项可得：

从式（33）可以看出，当升阻比增大时，Δψi的变化速度加快，为避免倾侧角发生过多的翻转，应增大航向角误差走廊；而当实际升阻比小于参考升阻比时，Δψi的变化速度放缓，为确保航向角误差能够及时地减小到终端误差要求范围内，应减小航向角误差走廊。

因此，设计补偿系数KL/D，i，利用对气动参数的估计对第2.3 节中式（9）的航迹方向角误差走廊Δψside，i(si)进行补偿：

式中：ΔψL/D，i(si)为修正后的航向角误差走廊。

在纵向制导过程中，可以通过调整迎角实现对升阻比的补偿，从而调整飞行过程的能量耗散速度，进而实现对升阻比变化影响协同飞行时间的补偿。根据文献［14］，飞行器升阻比随着迎角的减小先增大后减小，其临界点为最大升阻比迎角。因此，本文根据标称升阻比和剩余飞行时间-剩余能量剖面，提出了随协同飞行任务进程自适应变化的迎角PID调整策略：

式中：Δαi为迎角调整量；Δeres，i表示当前飞行器剩余能量；estd，i表示当前飞行器的标称剩余能量；∫(eres，i-estd，i)dt为调整策略的积分项为调整策略的微分项；k1、k2和k3是初始PID 增益，通过在PID 增益中加入随飞行时间变化的相关项，避免迎角调整量过大。

则实际迎角αi为：

式中：αstd，i为第2.3 节中式（16）预先设计的标称迎角。

注3.本节设计的航向角误差走廊补偿和迎角补偿的方法实际上是对本文第2节设计的协同制导律的补偿和进一步完善，能够有效提高制导系统的鲁棒性。

4 数值仿真

本文以CAV-H 飞行器［24］为研究对象，仿真过程的终端点约束为：落点经纬度为（105°，5°）；终端高度为20 km；终端速度为1 200 m/s。过程约束上限为：热流密度约束为1 400 kw/m2；动压约束为160 kPa；过载约束为4。迎角剖面的上下限分别为αmax=20°，αmin=8°；标称迎角的切换速度为vup=5 000 m/s，vdown=2 000 m/s；倾侧角取值范围是-80°～80°。为验证提出的时间协同鲁棒制导律的有效性，本文针对标称环境设计了不同的仿真任务，并针对参数不确定环境进行了蒙特卡洛仿真。

4.1 标称情况下的多机时间协同制导仿真

在标称环境下进行6架飞行器时间协同再入仿真，选择协同任务时间为tf=1 430 s。表1为该任务下各飞行器的再入初始条件。标称情况下的6飞行器时间协同制导仿真结果如图4所示。

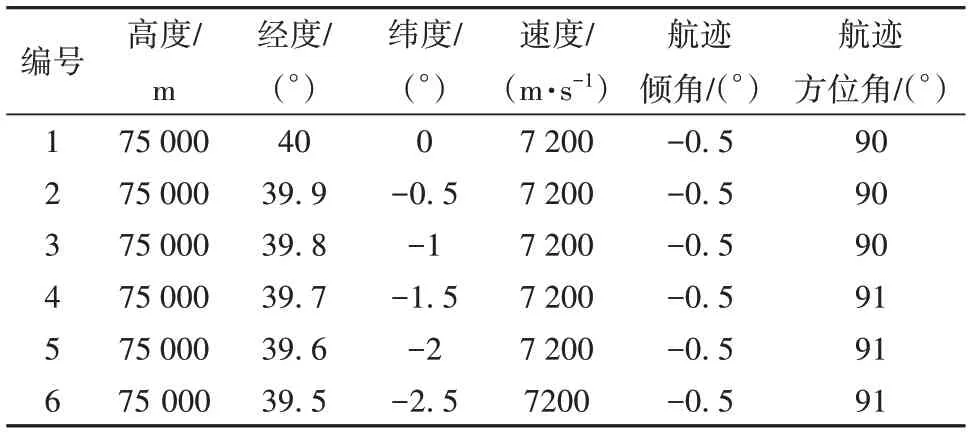
表1 标称环境下各飞行器再入初始条件Table 1 Initial condition for each vehicle during reentry under nominal circumstances

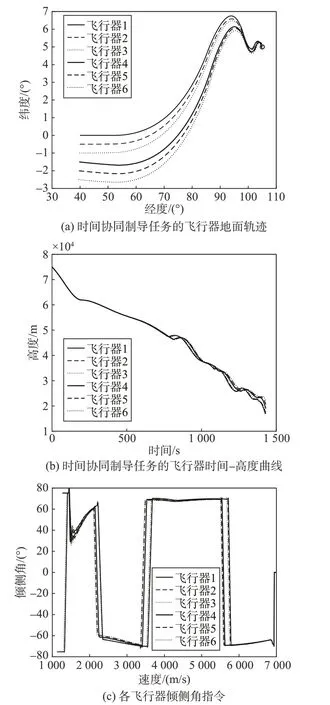
图4 标称情况下的六飞行器时间协同制导仿真结果Fig.4 Simulation results of time collaborative guidance for the six vehicles under nominal conditions

通过图4（a）和4（b）可以看出，本文设计的时间协同制导律可以有效地调整再入飞行器的飞行时间，实现不同起点的飞行器同时抵达目标位置。但在纵向制导的过程中，为了使协同任务满足时间约束，尤其是在飞行任务末段，在不加入迎角补偿策略的情况下会导致落点存在误差，终端高度误差在±2.5 km 以内。从图4（c）可以看出在本文设计的制导律作用下，飞行过程中的倾侧角没有进行频繁的翻转，有较好的工程可实现性。

4.2 存在参数不确定性条件下的时间协同鲁棒制导仿真

在参数极端变化的情况下进行3 架飞行器时间协同再入仿真，分别选取两种极端情况（情况1：CD-10%，CL+10%；情况2：CD+10%，CL-10%），对于飞行器1 和飞行器2 采用情况1，飞行器3 采用情况2进行验证。将未加入补偿策略的时间协同制导律（称为law1）与加入补偿策略的时间协同制导律（称为law2）进行对比。表2 为该任务下各飞行器的再入初始条件，协同飞行时间为tf=1 440 s。

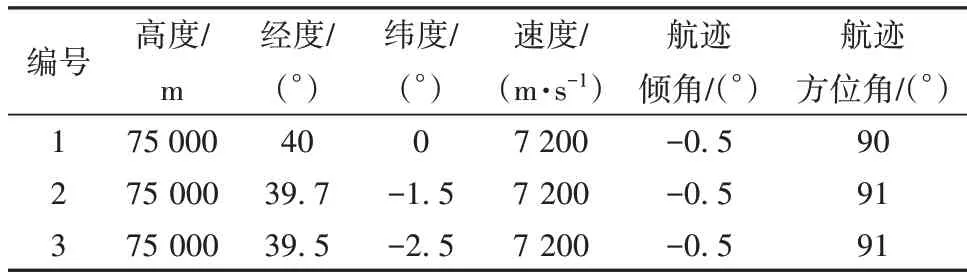
表2 各飞行器再入初始条件Table 2 Initial conditions for vehicles during re-entry

图5 是在不同条件下3 架飞行器的地面飞行轨迹对比结果。可以看出当升阻比增大时，飞行器1和飞行器2 能量耗散速度减缓，law1 制导律下的飞行器在协同飞行时间飞过了目标位置，而当升阻比减小时能量耗散速度加快，飞行器3 无法在规定时间内抵达目标位置，而law2 制导律在两种极端情况下都成功地使3 架飞行器抵达目标位置。结合图6飞行器的剩余能量曲线可以看出，本文提出的鲁棒制导律可以有效地改善飞行器能量耗散速度，实现对参数不确定性的补偿。

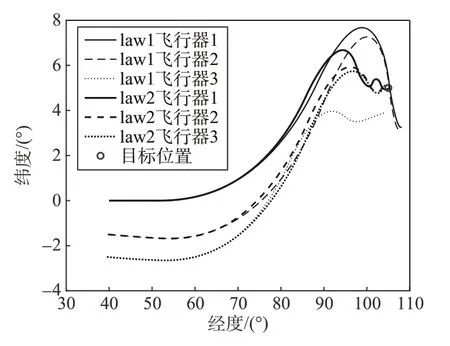
图5 参数不确定条件下的飞行器地面轨迹对比情况Fig.5 Comparison of vehicles' ground tracks under uncertain conditions

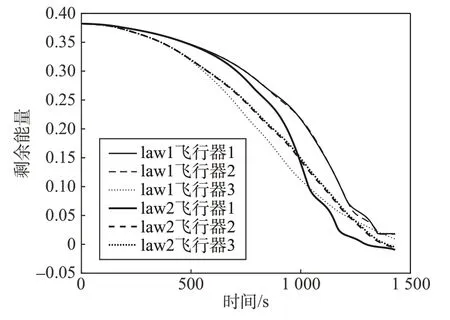
图6 参数不确定条件下的飞行器剩余能量曲线Fig.6 Curves of vehicles' remaining energy under uncertain conditions

图7（a）中不同情况下飞行器的迎角指令随着飞行任务进程调整量减小，尤其是在任务末段，补偿后的指令与标称迎角指令接近，避免了补偿量过大导致超过最大升阻比迎角的情况。从图7（b）中可以看出，law1 制导律在升阻比极端变化的情况下，由于剩余能量不足，难以抵达目标位置，制导指令出现了严重的震荡情况，而本文提出的协同鲁棒制导律的倾侧角指令均未发生剧烈震荡情况，翻转次数在7 次以内。图8 为了展示两种情况下的气动参数辨识结果，选择飞行器1 和飞行器3 作为代表。升阻比的估计值由升力系数和阻力系数估计结果计算得到，图中展示出本文的气动参数估计方法可以获得良好的估计结果，辨识误差较小。

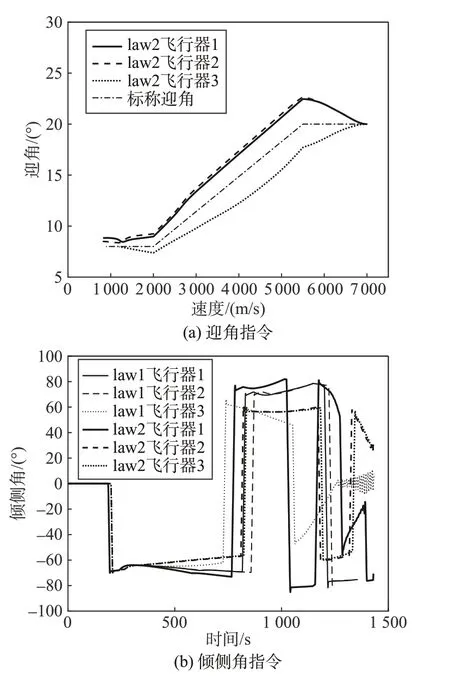
图7 参数不确定条件下的飞行器控制指令曲线Fig.7 Curves of vehicles' controlled variables under uncertain conditions

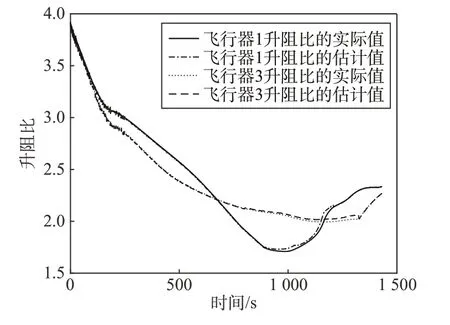
图8 气动参数的辨识结果Fig.8 The identification results of aerodynamic parameters

4.3 存在参数不确定性条件下的蒙特卡洛仿真

为了充分模拟协同再入过程的随机干扰和不确定性，对一些不确定量施加符合高斯分布的随机偏差如表3所示，选择协同任务时间tf=1 440 s，飞行器初始状态选择表与2的3架飞行器协同任务相同。

表3 蒙特卡洛仿真的随机偏差Table 3 Random disturbances in Monte Carlo simulations

在此条件下对本文制导算法进行了500次的蒙特卡罗仿真实验，具体结果如图9～11所示。

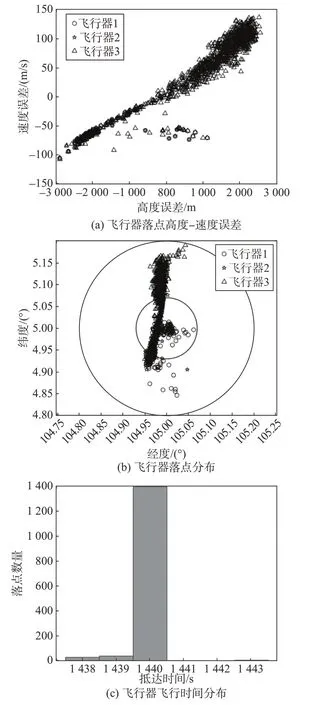
图9 蒙特卡洛仿真落点结果Fig.9 Terminal results of Monte Carlo simulations

图9 是蒙特卡洛仿真终端约束结果，在多种参数不确定条件下，终端高度误差在±2 km 以内，终端速度误差在±150 m/s 以内。终端位置误差基本在20 km 以内，落点时间误差不超过±3 s。以上结果表明本文制导方法在参数偏差条件下具有较好的精度和鲁棒性，能够满足协同再入制导的需求。图10给出了蒙特卡洛仿真的控制指令曲线。可以看出，在多种参数不确定的条件下，不同协同再入任务的倾侧角翻转次数不超过7次，有较好的工程可实现性。图11给出了蒙特卡洛仿真的过程约束曲线，可以看出在不同随机偏差影响的环境下，再入过程中的热流密度、过载、动压约束均未突破最大约束限制，保证了协同制导任务的安全性。

图10 蒙特卡洛仿真控制指令曲线Fig.10 Control variable curves of Monte Carlo simulations

图11 蒙特卡洛仿真过程约束曲线Fig.11 Curves of process constraints of Monte Carlo simulations

5 结论

本文针对存在参数不确定的多高超声速飞行器协同再入问题，提出一种时间协同的预测校正鲁棒制导方法。在横向制导过程中提出动态调整的航向角误差走廊，通过调整倾侧角翻转策略有效提高了飞行器的飞行时间调节范围。在纵向制导中通过提出的权值函数引入时间误差项，进一步实现对飞行时间的精准控制。通过结合基于改进无迹卡尔曼滤波算法的估计方法，对高超声速飞行器协同再入问题的不确定参数进行估计，并基于本文提出的标准能量-时间剖面，分别对航向角误差走廊和迎角进行补偿，有效改善了制导系统的鲁棒性。仿真结果表明，本文提出的制导方法为参数不确定条件下的协同制导问题提供了一种有效解决途径。