具有角度和时间约束的固定时间协同制导律
李鹤宇,王建斌,张锐,宋峰,姚雨晗,楼朝飞
(1.北京电子工程总体研究所,北京 100854;2.中国航天科工集团第二研究院研究生院,北京 100854)
0 引言
随着目标的机动能力大幅提高,传统的采用单飞行器一对一对抗方式很难发挥效果,采用多个飞行器协同作战,从多个方向同时撞击目标,能够有效降低对飞行器性能的要求并增加对目标的破坏概率[1]。为实现该目标,多飞行器协同制导方法受到越来越多的关注[2-4]。
多个飞行器同时撞击目标能够通过饱和攻击有效提升杀伤概率。文献[5]开创性地提出撞击时间控制制导律(Impact time control guidance,ITCG),实现多个飞行器具有相同的剩余飞行时间。文献[6]提出了一种基于两阶段序列凸规划的计算ITCG 算法,在发射前为飞行器设定飞行时间,以实现同时攻击。文献[7]考虑飞行器之间的通信拓扑,提出一种建立在视线坐标系(Line-of-sight,LOS)中的包含两个方向分量的协同制导律,实现在视线角度约束下同时攻击静止目标。上述算法针对静止目标。
文献[8]基于比例导引(Proportional navigation guidance,PNG),提出了一种多个飞行器对静止目标和机动目标进行协同对抗的协同制导律。文献[9]将局部滤波算法与协同制导律相结合以提升算法鲁棒性,从而确保在某些飞行器不可用的情况下,对机动目标的时间一致性。文献[10]提出了一种具有有限时间收敛性的三维协同制导律,该算法实现使用多个飞行器以预先指定的角度同时攻击同一目标。文献[11]利用时变终端滑模控制方法,设计了一种协同制导律,实现对机动目标的齐射攻击。文献[12]针对主从协同制导问题,采用超扭曲滑模控制方法实现剩余飞行时间误差在有限时间内收敛。文献[13]采用有限时间滑模控制理论和超扭曲控制算法实现具有时间一致性和视线角度约束的协同制导律,并扩展至领-从结构。文献[14]基于有限时间滑模控制理论提出一种有限时间收敛的协同制导律,但制导律中的符号函数会引起频繁的抖振和不连续性。文献[15]为实现制导律的快速收敛并减少抖振,将非奇异快速终端滑模控制应用到协同制导律设计中。上述算法的收敛时间取决于系统的初始状态,不能给出明确的量化表达式,限制了算法的应用范围。
固定时间收敛方法优点在于证明稳定性过程中,收敛时间与初始条件无关,因此得到广泛关注。文献[16]将通过定义误差项,将制导问题转化为跟踪问题,提出一种具有固定时间收敛的期望误差动力学方程。文献[17]针对存在未知但有界的匹配和不匹配扰动下的二阶系统,提出了一种滑模控制器,实现固定时间收敛性,该设计不需要使用扰动观测器对系统扰动进行观测,有效降低系统的复杂性。文献[18]研究全局鲁棒固定时间稳定性,提出一种指数系数包含常量和状态变量的具有鲁棒性的固定时间收敛的控制方法,并将其应用于一类包含有界干扰的非线性二阶系统,实现系统在固定时间内收敛。文献[19]针对多电机驱动系统的死区非线性,提出了一种包含固定时间滑模控制和高增益补偿器的两阶段控制方法,并针对系统中的扰动,设计了一种实用的固定时间收敛控制器,提高了方法的适用性。
固定时间收敛的协同制导算法相比有限时间收敛的协同制导算法具有更好的性能。本文提出一种针对机动目标、具有终端角度约束和时间一致性约束的固定时间收敛协同制导算法。
1 问题描述与基础理论
1.1 问题描述
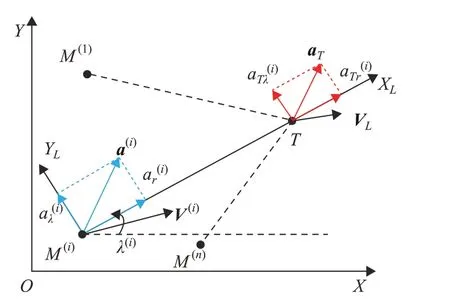
图1 二维协同制导示意图Fig.1 2-D cooperative guidance geometry
1.2 基础理论
1.2.1 通信拓扑
飞行器之间的通信关系由通信拓扑图定义为Ω(ν,ε),其中ν={1,2,…,N}是通信拓扑中的节点,代表飞行器,ε=ν×ν是通信拓扑中的边,一条边(i,j)(i≠j)表示第i个飞行器能够向第j个飞行器传递信息。定义通信拓扑的连接矩阵Α=[aij]∈RN×N,若(i,j) ∈ε,则aij=1,反之aij=0。定义通信拓扑的拉普拉斯矩阵L=[lij]∈RN×N,计算方法为:
如果对于任意的(i,j) ∈ε,(j,i) ∈ε成立,则称通信拓扑是无向的,如果通信拓扑中信息能够在任意两个节点间通信,则称通信拓扑是连通的。
引理1[20].如果无向图Ω(ν,ε)是连通的,则具有以下性质:
1)0是L的特征值,其对应特征向量为1N=[1,…,1]T。
3)λ2(L)xTx≤xTLx≤λN(L)xTx,∀x∈RN,λ2(L)和λN(L)表示除0外的L最小和最大特征值。
引理2[21].对于x1,x2,…,xN>0,0 <p≤1,q>1,则下式成立:
1.2.2 固定时间收敛理论
引理3[22].设非线性系统:
式中:f为连续方程,且f(0)=0。如果存在一个连续可微的正定径向无界函数V:RN→R+使得:
式中:a>0;b>0;0 <γ<1 <α。则非线性系统在零点全局固定时间稳定,并且过渡时间满足:
引理4[18].设非线性系统:
引理5[23].设非线性系统:
若|ω|≤L,L∈N+,构建如下观测器:
式中:Pl为李雅普诺夫方程PlBl+=-Ql的解,Ql为正定矩阵,l=1,2;Bl为:
本文做出如下假设:
假设1.协同制导算法能够实时获得第i个飞行器和目标之间的距离视线角视线角速率的真值。
自公安部制定并颁布实施《公安机关适用继续盘问规定》这个规范性文件以来,很多地方的公安机关对这项措施轻易不再适用,有的公安派出所甚至三年多来还从未适用继续盘问,取而代之的是传唤或拘传措施,继续盘问空置化的倾向比较严重;[5]经过有关学者的调研,在某地多起案件的办理过程中,无一起案件的办理对嫌疑人适用过继续盘问措施,进一步证明了当前继续盘问措施被空置化的现状;[6]孙志刚事件以后,公安部制定了《公安机关适用继续盘问规定》,此后在办理刑事案件时运用继续盘问的情况的调查统计结果显示有105人选择基本不用,比例高达78.95%。 [7]
假设2.目标的加速度作为系统的干扰项是未知的,在中制导段,相比目标和飞行器的距离r,目标加速度aT为小量,因此E,E∈R+;aT是mT阶可微的,且≤L,L∈R+,mT∈N+。
假设3.飞行器的通信拓扑是无向且连通的。
注1.由于:
1)雷达、飞行器携带的导引头能够有效探测目标信息,提供相对距离、相对速度和视线角信息,通过微分、滤波等计算,可以获得实时的视线角速率信息。
2)目标通过舵机、螺旋桨等执行机构进行机动,机动过程是一个连续、有界的过程,因此加速度是可微的。
3)飞行器之间能够利用通信设备发送自身的信息,接收其它飞行器的信息。
因此,假设1~3是合理的。
设X=[xi]∈RN,i=1,…,N,定义:
2 协同制导算法设计
设飞行器编号用上角标i表示,i=1,…,N。对飞行器沿视线方向和与视线垂直方向加速度进行设计,从而实现时间一致性约束和终端角度约束。
2.1 视线方向加速度设计
对视线方向加速度进行设计,使得每个飞行器的剩余飞行时间趋于一致,从而实现时间一致性约束。飞行器i的剩余飞行时间为:
对式(16)求导,并结合式(1)可得:
构建飞行器视线方向加速度为:
式中:αr>0,βr>0,0 <pr<1,qr>1。由式(16)、式(19)、式(21)组成的系统能够保证剩余飞行时间在固定时间内趋于一致[24]。
2.2 视线垂直方向加速度设计
定义状态变量:
式中:β,α1,μ1根据引理4 进行参数选择。构建飞行器视线垂直方向加速度为:
式中:k,α2,μ2根据引理4进行参数选择。
定理1.由式(2)、式(23)、式(24)组成的系统能够保证在固定时间内,视线角收敛至期望值。
证.对滑模面式(23)求导:
3 仿真校验
在仿真中,飞行器的总加速度被限制在200 m/s2,该算法主要为中制导段设计,设定3 个飞行器和目标的距离同时小于200 m时,仿真终止。
采用3 个飞行器对抗1 个目标的场景对本文提出的方法进行验证。飞行器之间的通信拓扑如图2所示。目标在发射系中的初始位置为(10 000,0) m,初始速度为(95,200) m/s,目标沿OX轴方向加速度分量为0,沿OY轴方向加速度分量aTy如图3 所示。3 个飞行器的初始状态如表1 所示,其中(x,y)和V均为发射系下的值,θ为速度矢量和发射系x轴的夹角,λd为期望的视线角。仿真结果如图4所示。
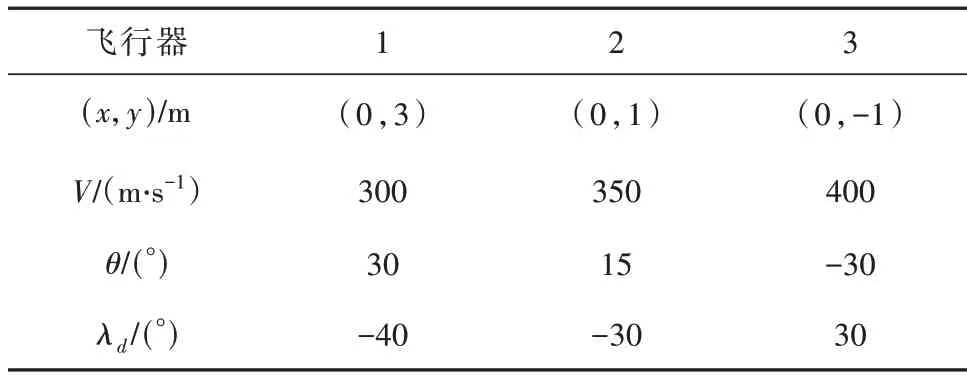
表1 飞行器初始状态Table 1 Initial state of the vehicles

图2 飞行器通信拓扑Fig.2 Communication topology among the vehicles
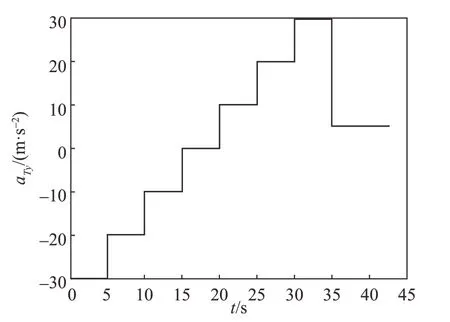
图3 目标加速度形式Fig.3 Target acceleration form
从图4(a)可以得出,使用本文提出的固定时间制导律,3 个飞行器可以从不同方向同时对抗目标。从图4(b)可以得出,飞行器1、飞行器2、飞行器3 的视线角分别在22.78 s、24.19 s、22.71 s 达到相应的期望值,本文提出的协同制导算法在视线垂直方向上,能够将视线角控制到期望值。从图4(c)可以得出,初始时刻,由于初始位置、初始速度的大小和方向的不同,剩余飞行时间在40~60 s之间,在7 s后,3 个飞行器的剩余飞行时间趋于一致,并保持到仿真结束。
4 结论
本文针对多飞行器对抗机动目标中的协同制导问题进行研究,利用分布式合作协议算法和滑模控制方法完成时间一致性约束和终端角度约束,实现固定时间收敛的协同制导律;此外针对目标加速度未知但有界的特点,通过设计滑模结构保证算法固定时间收敛,避免设计观测器,从而有效降低算法复杂性。通过仿真验证了本文算法的有效性。

