航天器姿态控制群体博弈分布式分配方法

刘浩然，叶东，肖楠，孙兆伟

（哈尔滨工业大学航天学院，哈尔滨 150001）

0 引言

随着微小卫星技术的不断发展，人们对小型化、集成化的卫星产生了较浓厚的兴趣，这种卫星可批量生产与快速响应［1］。但是这种小卫星由于体积与质量的限制，有时不能达到任务需求的性能指标。人们进而将注意力转移至由微小卫星构成的细胞星组合体。这种细胞星组合体由结构相同的众多独立细胞星组成，可根据任务的需要进行在轨组装［2］，并通过重构来替换功能失效的细胞星。细胞星组合体不仅可以组合成为一个新的个体执行任务，还能够附着在无法进行姿态控制卫星上，利用细胞星的执行机构进行姿态辅助控制［3-4］。这一功能有效地延长了失效卫星的使用寿命，使有效载荷能够发挥更大的效益。

每个细胞星自身都具有执行机构，如飞轮、推力器等。因此在对细胞星组合体进行姿态控制的时候，产生控制力矩的执行机构数目大于航天器的自由度［5］。这是一种冗余的力矩控制，这种控制方式具有鲁棒性强、提供的控制力矩大等优点。但是随着组合体中细胞星数目的增多，组合体结构不断变化，细胞星通间讯链路也愈加复杂，需要设计一种能够适应组合体结构变化的分布式力矩优化分配方法。

常用的冗余力矩控制分配法有：广义逆法，这种方法将执行机构构型矩阵的逆矩阵作为分配矩阵，是力矩最小的分配策略；链式递增法，这种分配方式考虑了执行机构的最大力矩输出限制［6］。另外，郭延宁等［7］研究了在执行机构最大力矩限制条件下的能量最优情况；何光宇等［8］使用遗传算法解决了力矩分配最优问题；张众正［9］在考虑能量消耗的同时，优化了执行机构的角动量裕度。近年来，博弈论方法也被用于多智能体的控制分配问题：Xiao等［10］将冗余控制力矩分配问题转化为多个模块卫星之间的微分博弈问题，通过求解二次优化问题实现力矩分配；柴源等［11］通过李雅普诺夫迭代法求解耦合状态相关黎卡提方程，组得到状态反馈控制器，从而实现及控制力矩分配；韩楠等［12］和罗建军等［13］通过各细胞星之间的合作博弈，达到了控制失效卫星的目的；常海涛等［14］提出了一种分布式能量均衡的冗余力矩分配方式，解决了集中通信信息负载大等问题；刘伟星等［15］给出了一种考虑飞轮角动量均衡的细胞星分布式力矩分配方法。上述分布式分配方法中，只考虑能量或角动量均衡度单一优化指标，并未考虑细胞星力矩输出能力。在本文构造非合作博弈的分布式群体博弈分配方法中，每个细胞星都输出相对较小的力矩使总输出力矩达到要求，并在分配过程中考虑到了输出能力及角动量裕度的限制。

不同于一般博弈，群体博弈不研究单个博弈参与者的策略选择，而是研究整个群体中的策略选择分布［16］。近年来它的主要研究领域是优化控制器设计［17］和资源分配问题［18］。例如，在无线通信网络中，在提供客户满意的服务质量的同时，尽量减少功耗［19］。同时群体博弈的动态资源分配方法还被广泛应用到城市供水系统［20］与电网系统的资源分配中［21］。Nash 均衡（NE）描述了群体中没有一方愿意单方面改变其策略的状态。群体博弈的最终目标是求解群体Nash 均衡，常用群体动力学求解群体博弈Nash 均衡。常用的群体动力学有复制器动力学、Smith动力学以及logit动力学。群体动力学充分利用了群体博弈中群体质量不变这一特点，能够对分配总量进行限制，但是无法直接对选择每种策略的群体质量进行限制。Sandholm［22］系统地总结了群体动力学与Nash 均衡之间的关系。Barreiro-Gomez等［23］建立了分布式群体动力学的广义形式，在分布式群体动力学下，群体博弈的Nash 均衡仍然是稳定的。Tan等［24］介绍了基于图论拓扑的复制动力学，总结了分布式Smith 动力学和logit 动力学的平衡点与Nash 均衡点之间的联系。群体博弈是解决分布式分配问题的一个有效手段。

本文将细胞星组合体力矩分配问题建模为群体博弈问题，提出一种基于群体动力学解决细胞星冗余力矩分配问题的方法。相较于传统群体博弈只利用群体质量对分配总量进行限制，本文通过收益函数的设计增加对每个策略分配量的限制，在考虑能量消耗的同时利用细胞星输出力矩能力与角动量裕度对细胞星分配到的力矩进行限制。同时本文设计的分布式力矩分配方法可以适应细胞星数目变化的情况。

1 组合体运动学与动力学

为方便后续描述引入如下坐标系：OΙXΙYΙZΙ表示惯性坐标系，是固连于惯性空间的坐标系；OiXiYiZi表示第i个细胞星的本体系；ObXbYbZb表示组合体本体系，即计算力较强的动力学计算卫星的本体系。

本文采用四元数对姿态进行描述，四元数q=[q0]∈R4表示每个航天器相对惯性系的姿态。qv∈R3是单位四元数矢量部分，q0∈R是标量部分。星群组合体的姿态运动方程为：

四元数qd=[q0]∈R4表示组合体期望姿态四元数，ω=[ωx ωy ωz]Τ为组合体惯性系下角速度。q×为q的叉乘算子，表示为：

引入误差四元数qe=[qe0]∈R4，计算公式如下：

式中：A为星群体系相对于期望系的坐标变换矩阵，

细胞星组合体动力学方程描述为组合体绕其质心转动的方程，每个细胞星都是刚体，引入刚体运动欧拉方程：

式中：ω×为ω的叉乘算子；J∈R3×3代表星群组合体的惯性矩阵；Ci∈R3×3表示由各细胞星参考系到惯性系的坐标变化矩阵；ui∈R3表示细胞星i提供的控制力矩。推导得出基于误差四元数的动力学与运动学方程：

为了实现细胞星组合体的姿态控制，本文设计了如图1的双层细胞星组合体姿态控制方案。

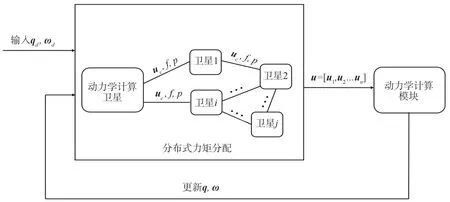
图1 姿态控制及力矩分配过程图Fig.1 Attitude control and torque distribution process

第1 层为控制力矩计算层，由1 个计算能力较强的卫星担任，它根据控制律计算出星群姿态控制所需要的总力矩uc。第2 层为基于群体博弈的冗余力矩分配层，该层对计算得到的总力矩依据卫星通信拓扑连接关系进行群体博弈力矩分配。每个细胞星只需向与其有连接关系的卫星传递总力矩uc、当前细胞星收益f、当前细胞星的群体状态p。

本文的重点为对冗余力矩分配方法的探讨，在控制律计算时采用基于PD控制的组合体控制律：

式中：kp，kd分别为PD控制的比例和微分参数。

2 力矩分配层群体博弈模型的建立

不同于传统形式的博弈，在群体博弈中，每一个参与者不被单独地对待，他们被视为组成一个连续的群体的一部分。在建立群体博弈模型时，本文将力矩分配系数作为博弈参与者，这个群体的总数用群体质量m=1 表示。细胞星作为策略集，用S={1，2，…，n}表示。系数分布作为群体状态，用矢量p=[p1，…，pn]Τ表示，其中p1，p2，…，pn为非负的标量，pi表示分配到细胞星i∈S的系数。选择每一个细胞星都有一定的收益，fi(p)表示选择细胞星i∈S的收益，那么群体博弈的收益非负向量表示为F(p)=[f1(p)，…，fn(p)]Τ。每一个细胞星是一个策略，分配系数在不同的细胞星之间进行选择，最后达到Nash 均衡。群体博弈模型与力矩分配概念关系如表1所示。

表1 群体博弈与力矩分配概念对照表Table 1 Concept comparison table of population game and torque distribution

当细胞星数目多的时候，并不是每个细胞星都能与其它所有细胞星进行通信。在群体博弈模型构建中，用带有策略限制的群体博弈模型来描述部分细胞星间存在通信障碍的情况。策略的限制可以用无向图G={ν，ε}来表示，其中节点集合v表征着可用的策略集，即v=S。边的集合ε⊂ν×ν描述了可以进行策略互动的策略。也就是说，若(i，j) ∈ε，则选择细胞星i的参与者可以与选择细胞星j的参与者进行博弈互动，反之则不能。

在本文所讨论的方案中，姿态控制力矩在时刻变化，导致群体博弈模型时刻变化。为了使群体更长时间处于Nash 均衡状态且减少细胞星间通信量，设计姿态控制力矩计算层，以一个T周期的时间间隔更新力矩。或者说，本地博弈模型的改变要有一定的时间间隔，在这个间隔内，总控制力矩大小不变，博弈模型不变。

群体博弈的收益函数是连续的。本文在设计收益函数时依据实际的应用，综合考虑了力矩输出裕度、能量消耗和飞轮角动量裕度。

首先，考虑飞轮力矩输出能力：

式中：pi表示分配到此细胞星的力矩分配系数为细胞星i坐标系到组合体坐标系下的坐标转换矩阵；uc为控制力矩计算层计算得到的所需总力矩；λi为分配增益系数；uimax为此力矩执行机构能够提供的最大力矩值；ucil为当前细胞星本体系下3 个轴中提供力矩的最大值。

其次，考虑飞轮能量的消耗：

式中：ki为一个足够大的常数，保证fi2(uci)的值始终大于0。λ2i表征该细胞星能量转换效率，值越大表明产生单位力矩所需能量越大，能量转化效率越低。

最后，考虑飞轮角动量裕度：随着力矩的产生，飞轮的角动量时刻变化，收益函数会产生一个关于群体状态的积分项，Nash 均衡值时刻变化，导致最后的群体状态在演化过程中无法达到Nash 均衡。用力矩更新时刻的角动量代替整个控制周期的角动量可以解决这个问题，设计的收益函数如下：

式中：Li表示控制力矩更新时的角动量绝对值；Limax代表飞轮最大的角动量；ci为确定正常数。第1 个式子表示的[0，Lu]段为期望工作范围，其收益是一个确定常数ci；第2 个式子表示的是飞轮角动量在一个比较大的区间中，收益随着角动量的增大而减小。当飞轮角动量达到最大值Limax，飞轮不能继续提供力矩，φi=0 可以有效避免这种情况。在一个控制周期0.5 s内，若飞轮以最大力矩输出，其角动量变化量为ΔLi，令Lui≤Lmaxi-ΔLi即可保证在该0.5 s 控制周期内角动量不能从期望工作范围达到饱和。

综合多个收益，令每个策略的收益函数为：

设计如式（11）的收益函数，可以避免输出力矩大于最大输出限制，以及角动量饱和等问题。

此外，细胞星在轨通常有数目及构型的变化，针对此情况，在细胞星数目增多时，可直接进行博弈分配；但当细胞星数目减少时，直接分离会导致该细胞星带走部分群体质量，导致分配系数的和小于1。故在细胞星脱离整体前，该细胞星的收益变为固定值0 而不是通过公式（8）-（11）计算得到，在此基础上细胞星再脱离组合体。

3 群体博弈模型的求解

本文利用群体动力学求解Nash 均衡，利用演化的思想求解群体博弈模型。群体动力学中一个重要的概念就是修订协议。修订协议可以看作一组允许参与者做出决定的规则，或者说，修订协议确定了个体改变其策略的条件。修订协议用ρ=[ρij]表示，它表示了不同策略之间的条件转换速率。给定一个群体状态p和一个收益向量F(p)，ρij(F(p)，p)表示了由策略i到策略j的条件转化率。可以得到这个群体状态的动力学方程：

等号右边第1项表示流入策略i的人数（从其他策略转化为策略i），第2 项表示从策略i中流出的总人数（从策略i转化到其它策略）。两者之差表示了策略i的群体状态变化量。根据不同的修订协议，群体动力学的微分方程也不一样。常用的群体动力学有Smith动力学和复制器动力学。

3.1 基于分布式Smith动力学的博弈模型求解方法

Smith动力学是两策略比较动力学，也就是在得到博弈机会时，随机选择一个策略进行比较，更改策略的速度只与策略之间的收益之差有关。换言之，只要对方策略的收益比当前策略收益大，那么博弈参与者就有机会改变其策略。Smith 动力学的修订协议为：

式中：[·]+=max(·，0)。将上述修订协议代入公式（1）中，得到关于此修订协议的动力学方程：

本文中，每个细胞星，即每个策略之间不是都相互连通的，采用限制策略的群体动力学方程变为：

式中：Ni={j∈S：(i，j) ∈ε} 表示在拓扑图中与策略i可以进行互动的策略。那么分布式Smith 动力学表示为：

引理1［23］.在Smith 动力学下，如果没有限制的群体动力学是渐近稳定的，同时策略之间拓扑关系是连通的，那么有策略限制的动力学也是渐近稳定的。且当动力学稳定时，当前群体状态就为群体博弈的Nash均衡解。

定理1.针对以式（8）-（11）为收益函数构建的群体博弈冗余力矩分配模型，基于Smith 动力学的修订协议构建如式（16）的分布式群体动力学，该动力学稳定且收敛于群体博弈的Nash均衡。

证.首先构造Lyapunov函数：

对Lyapunov函数求导：

为了描述∇Ψ(p)，给出下式：

式（19）表示Lyapunov 函数对pl求导。将式（19）代入式（18），得到：

式中：D(p)为fi1fi2的雅可比矩阵，形式为：

所以，D(i，i) ＜0，式（20）左侧第1 项小于0。在第2项中，根据修订协议ρji=[fi-fj]+，如果fi＞fj，那么fk-fi＜fk-fj恒成立；如果fi＜fj，那么修订协议ρji=[fi-fj]+=0。因此Lyapunov函数（p) ＜0，这个群体动力学是渐近稳定的。根据引理1，本文构造的收益函数所形成的分布式Smith 动力学是稳定的，且稳定值是群体博弈的Nash均衡解。

3.2 基于分布式复制器动力学的博弈模型求解方法

复制器动力学修订协议：

与式（13）相比，复制器动力学的修订协议不仅考虑不同卫星间收益函数之差，还考虑分配到对方卫星的力矩分配系数大小，也就是分配到更多分配系数的卫星更适合提供控制力矩。这个修订协议也被叫做两策略模仿。将上述修订协议带入群体动力学中得到关于此修订协议的动力学方程为：

采用策略限制的复制器动力学方程可以表示为：

引理2［22］.对于任意的x，y∈P，都满足(x-y)(fi(x) -fi(y)) ＜0 的群体博弈称为稳定博弈，稳定博弈以复制器动力学为群体动力学时，存在可收敛到唯一的Nash均衡解p*。

引理3［23］.在复制器动力学下，如果没有限制的群体动力学是渐近稳定的，同时策略之间拓扑关系是连通的，那么有策略限制的动力学也是渐近稳定的，且有策略限制动力学收敛于Nash均衡解。

定理2.针对以式（8）～（11）为收益函数构建的群体博弈冗余力矩分配模型，基于复制器动力学的修订协议构建如式（25）的分布式群体动力学，该动力学稳定且收敛于群体博弈的Nash均衡。

证.由式（11）及式（22）可得：

收益函数是关于群体质量负相关函数。对于任意的x，y∈P，都有(x-y)(fi(x) -fi(y)) ＜0，根据引理2 构造的群体博弈是一个稳定博弈，存在唯一的Nash 均衡解p*，并且该博弈策略之间的拓扑关系是连通的。根据引理3，所构造的群体博弈在有策略限制的复制器动力学下是渐近稳定的，且收敛于Nash均衡。

4 仿真校验

以分配系数作为群体质量，针对不同种类动力学修订协议进行仿真。考虑如图2的卫星拓扑图。

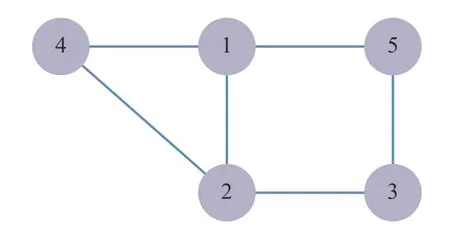
图2 卫星连接拓扑图Fig.2 Communicate topology among cellsats

系统总体转动惯量为：

细胞星的安装矩阵为：

给定初始姿态四元数为q1=[0.801 3 0.272 7 0.514 5 -0.136 9]T；初始角速度ω0=[0.01 0.02-0.03]Trad s；给定期望四元数qd=[1 0 0 0]T；期望角速度ωd=[0 0 0]T。力矩计算层更新力矩的周期为0.5 s；分配层各星之间通信间隔为0.02 s；给定各卫星最大输出力矩分别为6、5.5、6.5、6、7 N·m；飞轮角动量裕度分别为35、30、40、35、45 N·m·s；Lu=80%Lmax，λi=1，λ2i=1，ki=100，ci=1，kp=40，kd=90。1 号细胞星负责控制力矩计算。组合体输出力矩仿真结果如图3 所示，1 号细胞星输出力矩如图4所示。

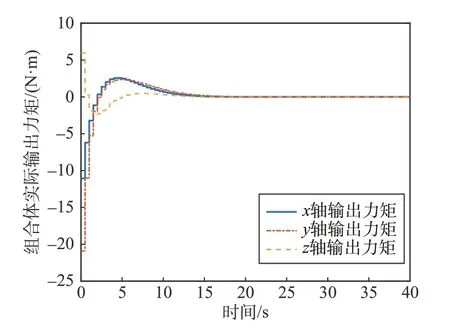
图3 组合体输出力矩Fig.3 Torque of combined body

为进一步剖析不同动力学对群体博弈收敛情况的影响，本文采用分布式Smith 动力学与分布式复制器动力学分别求解Nash 均衡，并对其进行比较。图5、图6 分别为复制器动力学与Smith 动力学求解过程中各个细胞星策略中的收益及其局部放大图。

图5 复制器动力学下收益Fig.5 Benefits under replicator dynamics

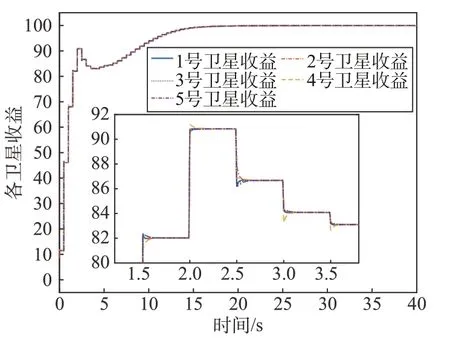
图6 Smith动力学下收益Fig.6 Benefits under Smith dynamics

由图像可以看出Smith 动力学与复制器动力学都收敛于同一个收益值，即同一Nash 均衡。但是两者的收敛速度有明显区别：在Smith 动力学下，收敛到Nash 均衡的时间要远远小于复制器动力学的时间。这是因为，在其它条件都相同的情况下，两种动力学的唯一区别就是二者的修订协议不同，Smith动力学的修订协议为ρij=[]fj(p) -fi(p)+，复制器动力学的修订协议为ρij=pj[fj(p) -fi(p)]+。修订协议可以看作一个博弈参与者在得到博弈机会时改变其策略的驱动力，驱动力与改变策略的概率成正比，即两者之间收益之差越大，这个驱动力越大，其策略改变的概率就越大，收敛越快。根据上述理论，Smith 动力学只需要考虑两者之间的收益之差，在一定范围内这个差越大收敛速度越快。而复制器动力学的收益不仅考虑策略间的收益差，同时还要考虑选择策略的群体，群体数多的策略可能更优，是一种从众模仿状态。本论文群体博弈中群体质量为分配系数，满足群体质量的和为1。所以对于任意pj＜1，在相同收益差的时候，驱动力减小会导致收敛速度变慢。另外由于可能存在次优策略有较多群体的情况，也会导致复制器动力学收敛速度较慢。

图7 是各细胞星分配系数与时间的关系，可以看出在前15 s 由于需要总力矩较大，收益函数之间差较大，细胞星会提供较大的驱动力。群体动力学收敛较快，分配系数变化明显。在15 s 后由于总力矩较小，各个细胞星分配到的力矩较小，导致收益函数之差较小，分配系数变化不明显。

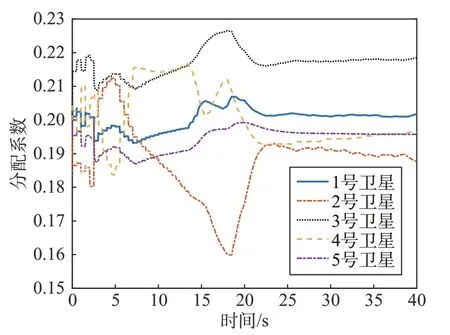
图7 各细胞星分配系数Fig.7 Distribution coefficient of each cellsat

为了体现本文方法的先进性，将本文算法与集中式能量最优的伪逆法和文献［14］的算法对比。相较于集中式能量最优算法，本方法细胞星在计算分配时只和与它相连的部分细胞星做信息交流，不用知道所有细胞星的状态信息，降低集中控制通信压力与通信延迟带来的误差。文献［14］给出了一种能量均衡的分布式控制力矩分配方法，通过优化能量平衡因子实现分布式力矩分配。评价细胞星提供控制力矩消耗能量指标为：

式中：ui为细胞星i输出力矩。在上述仿真条件下3种分配方法能量消耗指标如图8所示。

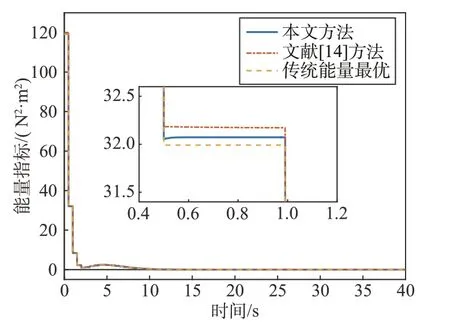
图8 3种分配方式能量指标图Fig.8 Energy index of three distribution methods

由仿真结果可以看出，在满足力矩输出能力限制的条件下，采用本文提出的方法与文献［14］所提出的方法能量消耗都近似于集中式能量最优分配方法，且在本文的工况下，本文方法的能量消耗小于文献［14］的分配方法。本方法相较于集中式能量最优方法能量多消耗0.41%，因为所设计博弈收益函数（11）利用力矩输出能力与角动量裕度对能量消耗进行加权，可以根据细胞星输出能力与角动量裕度对分配力矩大小进行限制，在满足限制的前提下，当消耗相同能量时，由可产生较大力矩的细胞星输出更多的力矩。而文献［14］与能量最优分配方法都没有考虑细胞星输出力矩的限制，细胞星分配到力矩存在大于最大输出力矩的情况，导致期望力矩与实际输出力矩间存在误差，定义细胞星组合体控制力矩输出误差：

式中：τ为细胞星组合体实际输出力矩。考虑细胞星间执行机构的差异，当1 号细胞星只能提供最大1.2 N·m 的力矩时，其它条件不变，图9、图10、图11分别为文献［14］、能量最优方法、本文方法细胞星组合体控制力矩输出误差图。

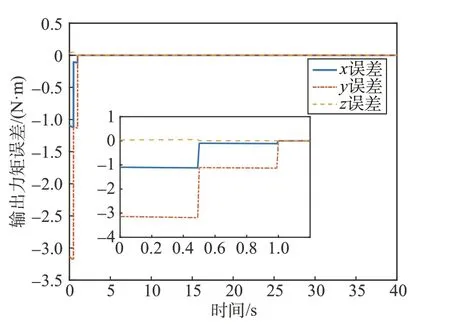
图9 文献［14］方法力矩误差图Fig.9 Torque error of the method in reference ［14］

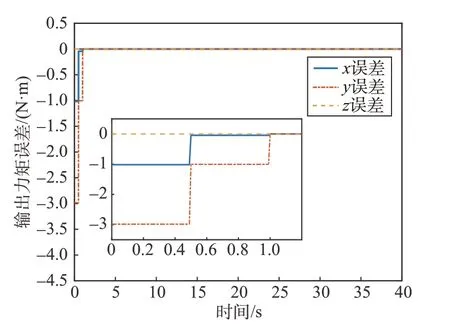
图10 能量最优方法力矩误差图Fig.10 Torque error of energy optimal method

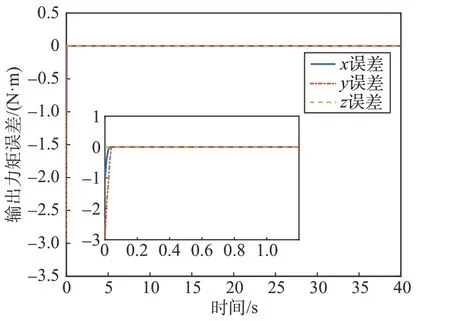
图11 本文方法力矩误差图Fig.11 Torque error of the method in this paper

由仿真结果可以看出，文献［14］及能量最优方法都未考虑细胞星输出力矩能力限制，组合体中存在输出能力较差的细胞星时，会存在较大的输出力矩误差。本文方法的仿真结果误差是由于初始化分配系数过大，1 号细胞星初始期望力矩大于u1max带来的力矩输出误差，但是在博弈过程中该细胞星的期望输出力矩快速减小。此外，文献［15］给出另一种分布式力矩分配方法，该方法在分配过程中以角动量均衡作为优化指标，考虑了飞轮卸载速度问题，但是同样在分配时没有考虑到飞轮输出能力的限制。当细胞星输出能力差异较大或对细胞星有严格的输出力矩要求时，会导致较大的输出力矩误差，本方法可以有效地解决这类问题。

接下来仿真细胞星数目变化的情况，设立如下场景：基于前文的仿真条件，在控制开始5 s后，第5颗细胞星脱离组合体，不参与力矩分配。第5 s时令5号细胞星收益为0，所得到的期望控制力矩如图12所示。

图12 5号细胞星期望输出力矩示意图Fig.12 Expect torque of No.5 cellsat

可以看出5号细胞星期望输出力矩很快降到0，实现了细胞星数目减少的目的。同理，此种方式也可适用于细胞星控制力矩执行机构失效的问题。在这种情况下，将失效细胞星收益调为恒定值0。

5 结论

本文主要研究了细胞星组合体的姿态控制力矩分配问题。

1）提出一种基于群体博弈的冗余力矩分布式分配方法，在对输出力矩无限制要求的前提下，能量消耗近似集中式能量最优分配方法，当组合体中细胞星输出力矩能力差异较大或存在输出能力较小的细胞星时，提出方法在分配时有较小的输出误差。

2）分析了求解力矩分配问题时，比较和模仿两种不同的演化策略，两种演化策略形成的不同的群体动力学可以收敛到同一Nash 均衡值。但在力矩分配系数之和为1的前提下，基于Smith动力学的分配收敛速度快于基于复制器动力学分配收敛速度。