指导学生录制数学讲题微课的思考与实践

广东省广州市真光中学(510380) 苏国东

1 问题提出

“学习金字塔”理论指出,学生不同的学习方式所达到的学习效果不同,以“能够将所学内容教授他人”的效果为最佳(学习内容平均留存率达到90%).对数学学科学习而言,学生讲题是一种有效的教授他人的学习方式,学生对他人讲授问题,不仅要对讲授内容作出独立思考,同时还要将内容转化为让他人理解的表达方式,在这过程中也提升了学生潜在智能的发展.

与教师讲题不同,学生讲题重在将问题的解法讲述清楚.在实际教学中,部分教师采取了在课堂上让学生直接上台讲题的方式,但碍于学生准备不充分、临场发挥不一、时间限制等原因,学生往往只能平铺直叙或轻描淡写,未能突出解题的重难点,缺乏小结的点睛之笔,讲题效果大打折扣.此外,台下学生虽然看似专注聆听,但未必能跟上讲题的节奏,课后也无法再次重温所学.

为解决上述问题,笔者尝试将学生现场讲题改为学生录制讲题微课的形式,原因有四点.一是能给予学生充分的思考和准备时间,发挥学习主体性,锻炼讲题能力;二是微课制作方便,大多数学生具有手机电脑等设备条件,在合适的时间和地点就可以录制;三是支持学生个性化学习,当学生遇到同类问题时, 可以随时播放相应的微课, 通过暂停、回放,学习和记录重难点;四是通过相互观看微课,能够有效促进师生、生生之间的学习交流.

2 微课录制的实施与成效

以最近一轮的微课录制实践为例,笔者指导了两个九年级教学班共70 余名学生在寒假期间开展了讲题微课录制活动.

在录制微课之前,笔者先给学生做好思想动员: 通过讲题既能加深对所学知识的理解和应用,又能提高逻辑思维能力和数学语言表达能力,每人录制一个微课,就可以获得70多个学习他人微课的机会,于己于彼都是一种交流提升;其次,告知学生对微课内容的要求: 自行选题,一个微课讲清一个问题,教会一类方法即可,无需面面俱到,微课时长一般控制在3-10 分钟,时间过短无法突出重点、讲透思路方法,时间过长则显得啰嗦拖沓,观众难以保持注意力;第三,教会学生简单的微课录制方法: 先熟悉所讲内容,列出讲题框架,借助ppt 制作讲题课件,再使用手机或电脑录屏软件进行录制,还可利用剪辑软件进行简单剪辑.让学生体会到录制微课的操作并不复杂,但要制作出优秀的微课作品,则要在选题、讲解和录制上下足功夫,从思想和行动上引起高度重视.

学生初期制作的微课难免存在一些问题,例如多数微课是顺着课件直接读出解题过程,语言平淡,缺少引导和小结;有的微课因为选题过于简单,时长只有1 分钟左右,缺乏讲题的必要.在教师的及时指导下,后续的微课质量逐步提升,不少微课能选择典型问题,讲解中增加启发式的设问和引导,结尾对解题方法或知识要点作出小结;也有个别微课采用纸笔手写、手机录像的方式来讲解压轴问题,代替了制作课件的繁琐,手写过程也更能引起观众共鸣;更有部分微课采用模拟对话的形式,在所讲问题的前后增设引例或变式题,形成一个个的微专题教学,学生的创意和动手能力实在让人惊叹.

这一轮活动下来,每个学生基本都参与了微课录制,有的学生还一连录制了三个,最终形成了115 个微课作品,笔者将这些微课上传到共享平台, 供两个班的同学观看学习.后续经师生投票又评选出36 个优秀作品,笔者选取了个别微课在开学后的复习课上进行播放,部分微课留给学生课后观看,巩固复习效果.录制讲题微课极大地激发了全体学生学习的积极性,增强了学生学习数学的自信心,不少学生还会利用课间时间在班级电脑上观看微课,相互研讨提高,数学学习氛围日趋浓厚.

3 讲题微课的流程与类型

综合分析学生的优秀微课作品,可以发现其讲题流程一般包括三个基本环节.如图1,一是提出问题环节,呈现微课的主旨问题或思考;二是解决问题环节,将大问题分解为若干小问题,或多个同类问题采用同种解法,或对一个问题给出多种解法等;三是小结方法环节,对解题用到的知识、方法或策略进行小结提炼,或引申出更多的思考.也有根据讲解内容的特点,在解题过程中以题点知,适时归纳方法,或采用先介绍知识方法,再进入具体情境解决问题的方式.

图1

根据学生讲题内容指向的不同,可将讲题微课大致分为问题讲解、知识梳理、综合压轴、拓展应用等四种类型.

3.1 问题讲解类

问题讲解类微课,是以一道或几道典型问题为载体,分析解题思路,讲解解题过程,归纳总结解题方法的微课.近期课堂教学或作业中的例题或习题, 是学生讲题的首选素材,这也是学生对刚习得的知识最直接的应用与转化.

例如,人教版数学九年级上册教材第87 页的例4 是圆与角平分线结合的典型问题,运用到圆的有关性质、勾股定理、构造辅助线等方法解题,不少学生在学习之后对此题的解法颇有体会,纷纷录制出讲题微课.以其中的微课“圆与角的平分线”为例,视频时长4 分10 秒,学生呈现了两种不同的解法,并小结得出解决此类问题的常用策略.

(1)呈现例题

如图2,⊙O的直径AB长为10,弦AC长为6,∠ACB的平分线交⊙O于点D,求CD的长.

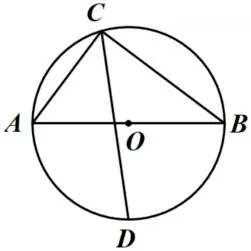
图2

(2)解决问题

解法1 如图3,连接AD,DB.因为AB是⊙O的直径AB,所以∠ADB= ∠ACB= 90°,CB= 8.把∆ADC绕点D顺时针旋转90°得到∆BDC′,则∠CDC′=∠ADB=90°,∠CAD= ∠DBC′,BC′=AC= 6,DC=DC′.因为∠CAD+∠CBD= 180°,所以∠DBC′+∠CBD= 180°,C,B,C′三点共线.所以CC′=CB+BC′=14.在等腰直角∆CDC′中,

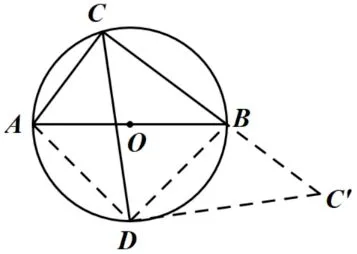
图3

解法2 如图4, 作AN⊥CD于点N, 作BM⊥CD于点M, 连接AD,DB.因为AB是⊙O的直径AB, 所以∠ADB= ∠ACB= 90°,CB= 8.因为CD是∠ACB的平分线, 所以AD=BD, ∠ACD= ∠BCD= 45°,∆ACN和∆CMB是等腰直角三角形.由勾股定理得易证∆AND∆DMB, 所以

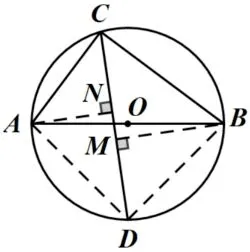
图4

(3)方法小结

①旋转(构造等腰三角形)⇒等线段共顶点; ②构造三垂直全等⇒转换线段.

(4)解题策略

①关注弧、弦、圆心角、圆周角的转换; ②善于利用特殊模型,构造辅助线,利用旋转转移角度和线段; ③灵活运用直径所对的圆周角等于90°、圆内接四边形、旋转等性质.

3.2 知识梳理类

知识梳理类微课,是在一定的学习阶段结束时,通过问题或情境回顾,对零散的知识进行归纳梳理,增强知识间联系的微课.能帮助学习者完善知识和方法系统,提升综合运用相关知识解决问题的能力.

以学生录制的微课“二次函数之abc 问题”为例,视频时长3 分47 秒,在学习完二次函数的图象与性质后,学生通过以题点知的方式, 在解题过程中回顾梳理了二次函数的系数、图象与性质之间的关系,最后小结解题的步骤与方法.

(1)呈现例题

已知二次函数y=ax2+bx+c的图象如图5 所示,对称轴是直线x=1,则下列结论中正确的有____(填写正确的序号).

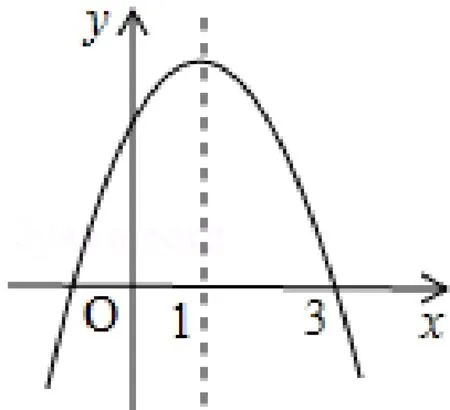
图5

①abc> 0; ②方程ax2+bx+c= 0 的两个根是x1=-1,x2=3; ③2a+b=0; ④当x>0 时,y随x的增大而减小.

(2)以题点知

二次函数开口方向反映a的符号, 本题函数开口向下,所以a<0;对称轴的位置反映a与b符号的异同,本题对称轴在y轴右侧,所以a与b符号相反,b>0;二次函数与y轴的交点位置反映c的符号,本题函数与y轴的交点在y轴的正半轴,所以c>0,故abc<0, ①错误.

方程ax2+bx+c=0 的根即是二次函数y=ax2+bx+c与x轴交点横坐标的值.因为二次函数的对称轴是直线x= 1,与x轴的一个交点为(3,0),根据对称性可得其与x轴的另一个交点为(-1,0),所以方程ax2+bx+c=0 的两根是x1=-1,x2=3,故②正确.

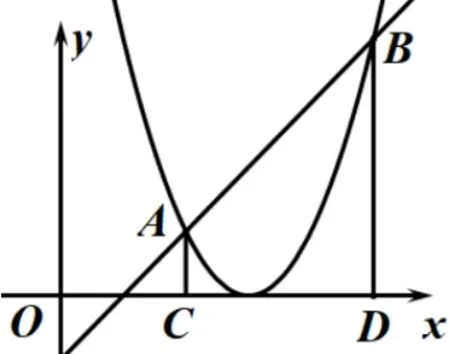
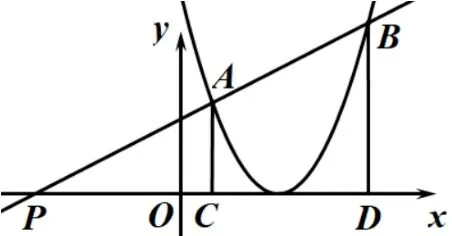
因为二次函数开口向下,所以在对称轴右侧,即当x>1时才有y随x的增大而减小,而当0

(3)方法小结

①认真审题; ②有图象的看图象, 没图象的要画出草图; ③从题目和图象中提取出已知条件; ④根据抛物线系数与图象性质的关系, 逐个选项计算和判断.

3.3 综合压轴类

数学压轴题具有综合性强、解法灵活等特征,考查学生对知识定理和方法技巧的掌握程度,以及分析和解决问题的综合能力.优等生对录制综合压轴题微课颇感兴趣,而且对讲法的设计做到精益求精,学生通过录制微课,既增强了解决难题的自信心,又激发了不懈的探索钻研精神.

以学生录制的微课“韦达定理在定值问题中的应用”为例,视频时长8 分钟,学生从引例到例题,由浅入深地讲述了定值压轴题的解答过程,最后小结利用韦达定理解题的方法.

(1)呈现引例

如图6,若函数y=x2-6x+9 与y=x-1 交于A,B两点,过点A作AC⊥x轴,过点B作BD⊥x轴,求OC+OD与OC·OD的值.

图6

分析 设A(x1,y1),B(x2,y2).由得x2-7x+10=0,所以x1=2,y1=1,x2=5,y2=4,即A(2,1),B(5,4).

因为OC+OD=x1+x2,所以OC+OD= 7,同理OC·OD=x1x2= 10.由此发现,本题不必具体求出两根,只需利用韦达定理得出两根之和与两根之积,即可代入求解.

(2)呈现例题

如图7,抛物线y= (x-2)2.直线y=kx+3k交抛物线于点A,B,交x轴于点P,AC⊥x轴于点C,BD⊥x轴于点D,求PC·PD的值.

图7

分析 设C(x1,y1),D(x2,y2), 则OC=x1,OD=x2.因为直线y=kx+ 3k过点P(-3,0), 所以PC=3 +x1,PD= 3 +x2,PC·PD= (3+x1)(3+x2) =x1x2+3(x1+x2)+9.由得x2-(k+4)x+(4-3k)=0,所以x1+x2=k+4,x1x2=4-3k,所以PM·PN=4-3k+3(k+4)+9=25.

本题通过化简得知PC·PD可以用含有两根和与积的式子表示,故利用韦达定理即可代入解题.

(3)方法小结

韦达定理反映的是两根之和与两根之积的形式.在解决有关问题时,有时可以不直接求出两根,而是找到式子中对应的几何意义或实际意义,借助韦达定理间接解决相关数量或长度之间的运算求值问题.

3.4 拓展应用类

拓展应用类问题,要求学生基于已有的知识和能力储备,在新情境或新问法下,调用新方法或新工具创造性地解决问题.通过录制拓展应用类微课,能开拓学生的知识视野,培养思维的灵活性和敏捷性,更能锻炼学生的自学自研能力,以点带面促进全体学生的数学学习.

以学生录制的微课“同底等周长的三角形中等腰三角形面积最大”为例,视频时长3 分52 秒,学生根据命题条件画出图形,转化为用数学语言表示并给出证明思路,小结环节更采用了设问的形式,激发学习者对问题进一步思考探究.

(1)呈现命题

在同底边并且周长相等的三角形中,等腰三角形的面积最大.

(2)数学表示

根据命题条件,以AB为公共底边,在同侧画出一个等腰∆ABC和任意一个非等腰∆ABD.则可以将命题表示为: 如图8,已知∆ABC中,AC=BC,∆ABD与∆ABC的周长相等,求证S∆ABC>S∆ABD.

图8

(3)证明命题

如图9, 过点C作l//AB, 延长AC到点B1, 使得CB1=CB, 则有∠1 = ∠CAB= ∠CBA= ∠2.连接BB1,B1D, 则l是线段B1B的垂直平分线.因为∆ABD与∆ABC的周长相等, 即AC+BC=AD+DB, 所以B1D+AD>AB1=AC+CB1=AC+CB=AD+BD,因此B1D>BD.因为点D和点B在l的同一侧,点D到AB的距离小于点C到AB的距离,所以S∆ABD

图9

(4)小结思考

解决这个问题的过程中用到了哪些数学知识和数学思想方法? 你还能提出相关的变式问题吗?

4 结束语

学生录制数学讲题微课的教学实践,不仅克服了传统讲题方式的局限性, 有效提升了学生的数学素养和创新能力,更为学生搭建了一个自我展示与学习交流的重要平台.展望未来,我们将持续深入探索和完善学生录制讲题微课的教学方式,引导学生更注重解题思路和方法的规范表达,以使讲题的形式和内容更加丰富多彩.同时,我们将引入更为先进的教育技术手段,使学生能够更便捷地进行微课创作和分享,催生出更多高质量的作品资源.进而有力推动师生数学学习共同体的形成与发展,为数学教育的改革与创新注入新的活力.