基于GeoGebra 的解析几何中一类蝴蝶模型的探究与推广*

江苏省常州市第二中学(213003) 王 强

解析几何是用代数方法研究几何问题的数学分支科学,既是近现代数学的重要内容,又是高中数学课程的主干内容.平面解析几何综合题是每年高考的必考题型,也是高中数学教学的难点之一,其研究方法是通过建立几何图形的代数方程(或不等式),实施代数运算,并由代数运算的结果得到几何图形的性质.法国著名雕塑家罗丹曾说: 生活中不是缺少美,而是缺少一双发现美的眼睛.学习数学,我们也要培养一双发现美的眼睛.以近三年的全国高考题为例,我们发现每年都有一些美丽的解析几何模型值得我们深入探究,通过探究我们可以充分感受到圆锥曲线的和谐统一之美.笔者以一道2022 年全国甲卷理科的解析几何题作为探究情境,开设了一节校际公开课“圆锥曲线中一类蝴蝶模型的探究”,现将教学过程和教后反思整理如下,恳请读者不吝赐教.

1 挖掘真题启示,创设模型情境

教师呈现近年新高考全国卷解答题中美丽的解析几何模型,如2020 年的新课标I 卷的“燕尾”模型(图1),2021 年全国甲卷的“眼睛”模型(图2),并结合GeoGebra 软件制作的动画,进一步将真题结论进行一般化推广,让学生初步感受圆锥曲线的图形美和统一美.

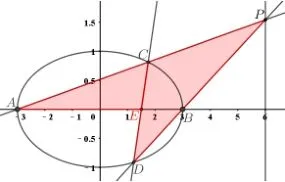
图1“燕尾”模型

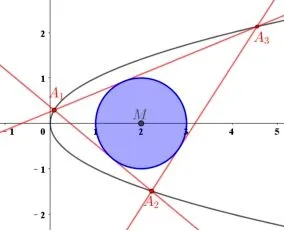
图2“眼睛”模型

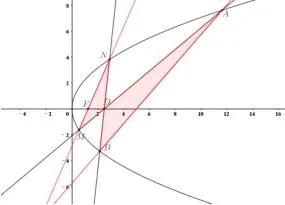
图3 抛物线中的“蝴蝶”模型

题目呈现(2022 年全国甲卷理科20)设抛物线C:y2=2px(p>0)焦点为F,点D(p,0),过F的直线交C于M,N两点.当直线MD垂直于x轴时,|MF|=3.

(1)求C的方程;

(2)设直线MD,ND与C另一个交点分别为A,B,记直线MN,AB的倾斜角分别为α,β.当α-β取得最大值时,求直线AB的方程.

2 顺应学生思维,探究解决模型

师: 这节课我们一起探究圆锥曲线中这类“蝴蝶模型”.(学生思考片刻后,请学生交流解题思路.)

师: 生1 对抛物线的定义运用的比较好.那么第二问同学们是如何思考的呢?

生2: 因为直线过点F(1,0), 所以可设直线MN:x=my+ 1, 代入y2= 4x, 可得y2- 4my- 4 = 0, 设M(x1,y1),N(x2,y2),则∆>0,y1+y2=4m,y1y2=-4.

当直线MN斜率不存在时,由对称性知直线AB斜率也不存在,此时α-β=0.

当直线MN斜率存在时,则直线AB斜率存在,分别记直线MN和AB的斜率为k1,k2,则k1= tanα,k2= tanβ,所以.后面我就没有思路了……

师: 生2 利用了转化的方法将α-β的最值问题转化成了tan(α-β)的最值问题,进一步转化成了与两直线的斜率相关的二元的最值问题.我们继续思考研究二元最值的一般方法是什么方法?

生2: 消元法.

师: 消元法的前提是知道k1和k2之间的关系,最理想是知道k1和k2的等量关系,你能根据图形直观大胆提出猜想吗? 大家一起讨论下.(讨论过后,请学生代表生3 谈猜想)

师: 生3 从四则运算的角度大胆提出了四个猜想,并借助图形的对称性和直观性,否定了前三个,那么是否为定值呢?

教师操作GeoGebra 课件, 通过移动滑动条改变直线MN,观察直线MN和直线AB的方程的变化(图4),发现直线MN的斜率是直线AB的斜率的2 倍, 猜想(注: 为了便于观察,需要在GeoGebra 中设置直线方程的形式为y=kx+b)

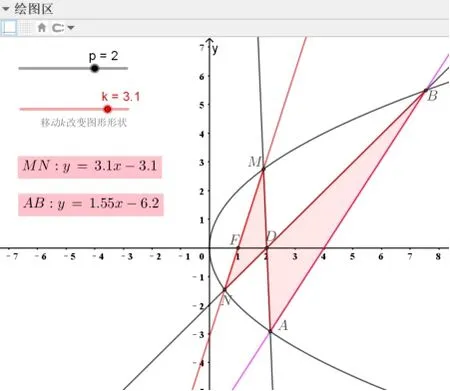
图4 斜率之比为定值

师: 生4 借助已知一点算另一点的方法得到了点A和点B的坐标,从而证明了,进一步消元,并利用基本不等式求出了取得最大值时直线AB的斜率,推理过程中有值得商榷之处吗?

生5: 用基本不等式求最值时, 应注意“一正二定三相等”,还需要对k2的正负进行讨论,由斜率和倾斜角的关系知,若k2<0,则α<β,此时α-β为负值,然后讨论k2>0.

师: 生5 关注到了应对k2的正负进行讨论,思考很全面.通过前面的求解我们已知直线AB的斜率为,求直线AB的方程还需要求什么量? 你能提出你的猜想吗?

生6: 还需要求直线上一点,有可能直线AB过某一定点.

师: 定值定点问题是我们平时研究的重点.如果直线AB过定点,你能预判定点的位置吗? 为什么?

生7: 由椭圆的对称性,定点在x轴上.

教师让生7 上台操作GeoGebra,设置追踪直线AB,移动滑动条(图5),发现直线AB交于一定点(4,0).

图5 直线过定点

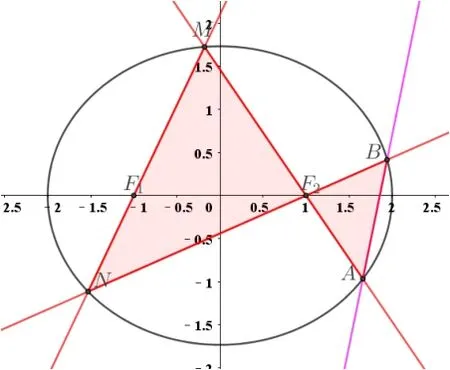
图6 椭圆中的“蝴蝶”模型

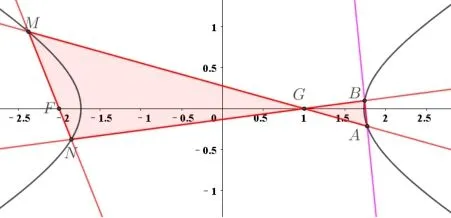
图7 双曲线中的“蝴蝶”模型

追问: 借助GeoGebra 的动态呈现,我们发现直线AB过定点(4,0).我们能不能用解析法进行论证呢? (学生独立推理后,投影学生的解答.)

师: 在生8 证明定点的过程中,令“y=0”是非常关键的一步,利用图形特征如椭圆的对称性起到了简化运算的作用.回顾解题过程,我们发现运动变化中往往蕴含了不变,化动为定是我们求解问题的方向,以形助数是我们简化运算的方法.

3 自主生成问题,类比推广模型

师: 开普勒(数学家、物理学家)曾说“数学就是研究千变万化中不变的关系”,定值定点问题也是高考的热点.根据圆锥曲线的内在统一性,通过类比你能提出椭圆或双曲线中可能成立的定值定点结论吗? (教师利用GeoGebra 课件与学生互动,共同生成新问题.)

猜想1: 已知椭圆E:左、右焦点分别为F1,F2,过F1的直线交E于M,N两点.设直线MF2,NF2与椭圆E分别交于A,B两点.

(1)当直线MN,AB的斜率存在时,分别记为k1,k2,求证:为定值;

(2)求证: 直线AB恒过定点.

猜想2: 已知双曲线E:左焦点为F,过F的直线交E于M,N两点.已知G(1,0),设直线MG,NG与E另一个交点分别为A,B.

(1)当直线MN,AB的斜率存在时,分别记为k1,k2,求证:为定值;

(2)求证: 直线AB恒过定点.

实际教学中学生生成新问题后,只证明了猜想1 的定值,定点留作课后思考.因为篇幅所限和证法的相似性,留作读者自行证明.

4 提炼模型算法,生成探究作业

师: 你能画一幅图来提炼蝴蝶模型的算法吗?“学生”就是学会不断生出问题的人.将问题“一般化”是数学研究走向深入的一般方法,你还能提出新的更一般的问题吗?

学生课后通过研究小组的共同探究,利用GeoGebra 先猜再证得到了如下三个性质,通过研究充分感受到了圆锥曲线的和谐统一之美.

性质1 若过点M(m,0) 的直线与抛物线C:y2=2px(p> 0)交于点A,B,点N(n,0)直线AN,BN分别交抛物线C于点P,Q,则直线PQ过定点

若直线AB和PQ的斜率均存在,且

5 技术辅助教学,促进素养生成

《普通高中数学课程标准》在教学建议中指出应重视信息技术运用,实现信息技术与数学课程的深度融合.[1]章建跃教授提出“四个理解”是落实核心素养的关键,“理解技术”就是要懂得如何有效利用技术帮助学生的学和教师的教.本节课充分融合动态几何软件GeoGebra,在一类抛物线的最值问题探究中利用GeoGebra 的动态呈现发现定值定点的存在,借助几何图形直观指明代数运算方向.利用类比、推广、一般化的数学研究方法,从模型的视角进一步思考问题,推广得到这类蝴蝶模型在椭圆和双曲线中的性质.

数学建模是对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题的素养.[1]数学建模的第一阶段是通过利用数学的眼光发现问题,借助数学的思维分析问题,通过数学的语言表达问题,从而构建数学模型,实现从现实世界到数学世界的过渡.在日常教学中我们应增强模型的意识,融入建模的思想,如本课例中基于GeoGebra 软件利用数学的眼光(动中找定)发现定点定值的存在,借助数学的思维(从特殊到一般)深入探究模型,通过数学的语言(性质1∼3)表达推广得到的结论.

2019 年国务院办公厅发布的《关于新时代推进普通高中育人方式改革的指导意见》中指出,应“提高作业设计质量,精心设计基础性作业,适当增加探究性、实践性、综合性作业”.GeoGebra 软件为开展数学探究性作业搭建了平台,如本探究中性质1∼3 的发现和证明,学生利用GeoGebra 的直观呈现发现性质的可行性,进一步用解析法推证后,利用GeoGebra 的数值计算验证性质的正确性.通过探究性作业可以提升学生发现问题、提出问题、分析问题和解决问题的能力,起到减负增效的作用,促进核心素养的生成.

数学可视化就是“看见不可见”, 即将抽象的数学对象用可看见的表征形式清楚直白地呈现出来,从而得到一个形象、直观、整体的认识和理解.[2]利用GeoGebra 可以将抽象的方法直观化,帮助学习者洞悉问题本质.从这类蝴蝶模型的探究课例中笔者深切感受到GeoGebra 软件不仅是几何图形动态展示的强大助手,也是数学探究性作业实施的有力后盾,更是理想的深度学习平台和深度教学工具.在新课改中我们应加强提升自身的信息技术素养,更好地利用技术促进教与学,这也是数学教师专业成长的必经之路.