关于新中考背景下学生发展代数推理能力的几点思考*

广东省东莞市松山湖北区学校(523808) 张海营

随着中考制度改革,广东省中考全省统一命题呼声越来越高.2023 年3 月8 日,广东省教育厅发布了《关于公开征求深化高中阶段学校考试招生制度改革实施意见》的公告,拟从2024 年起初中学业水平数学考试将由省级统一命题,笔者结合20 余年一线教学工作经验,就广州、深圳中考自主命题和省卷作对比研究, 发现代数推理在试题中占较大比重,如2021 年广东省中考第25 题、2023 年广州市中考第24 题、2023 年重庆市中考第18 题等,此类代数推理题型蕴含演绎推理、情境推理、归纳推理和条件推理等思想方法,极可能成为下一阶段广东省统一试卷命题的热点方向.

推理是数学的基本思维方式,也是人们学习和生活中经常使用的思维方式.代数推理题是以代数知识为主或以代数变形技巧为主的一类数学问题,推理过程是从条件出发,由代数定义、代数公式、运算法则和运算律得到结论(特定的目标结构或关系)的一种变形和转化[2].

1 演绎推理题

推理既包括合情推理,也包括演绎推理,因此特殊化和一般化也应成为代数推理的一项基本技能.演绎推理则是从已有的事实(包括定义、公理、定理等)出发,按照规定的法则(包括逻辑和运算)证明结论,这种推理严密到滴水不漏,演绎推理要求尽量还是循序渐进,中考考查及评卷严谨,历年考查主要突出推理能力及运算能力[3].

2 情境推理题

情境推理题解题时,往往会从题干信息中找到答案,合理筛选出有效信息,排出干扰信息,挖掘潜在信息进行类比迁移.2023 年各省市数学中考特别突出对新情境下数学知识的考查,突出“无情境、不命题”的命题思路,引导一线教师从具体情境中抽象出数学符号的过程及用代数式进行表述的方法例,逐渐形成推理能力,培养学生的科学精神.

例2.1 (2023 重庆市中考第18 题)对于一个四位自然数M,若它的千位数比个位数多6,百位数比十位数多2,则称M为“天真数”,如: 四位数7311,∵7-1 = 6,3-1 = 2,∴7311 是“天真数”; 一个“天真数”M的千位数为a, 百位数为b,十位数为c,个位数为d,记P(M) = 2(a+b)+c+d,Q(M)=a-5,若能被10 整除,则满足条件M的最大值为.

3 归纳推理题

3.1 等差规律

例3.1.1 (2019 年广东省中考第16 题) 如图1 所示的图形是一个轴对称图形,且每个角都是直角,长度如图所示,小明按图2 所示方法玩拼图游戏,两两相扣,相互间不留空隙, 那么小明用9 个这样的图形拼出来的图形的总长度是____(结果用含a、b代数式表示).

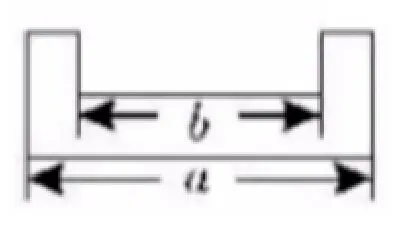
图1

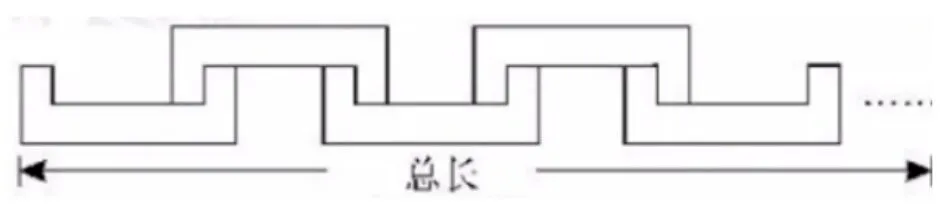
图2

解析 由题意,第1 个图形的总长是a+0·b=a;第2 个图形是a+1·b=a+b;第3 个个图形是a+2·b=a+2b;第4 个图形是a+3·b=a+3b;第5 个图形是a+4·b=a+4b;……因此图形变化规律是a+(n-1)b;故第9 个图形拼出来的总长度为:a+(9-1)b=a+8b.

点评 数列问题是高中学习重点内容,也是初高中知识衔接的桥梁.本题属于简单常规题型,通过基本数字变化规律可得到答案.通过对一些基础的知识点或数学概念进行变形,给学生以一定规律排列的数,但其中至少缺少一项或是给几个图形规律最后转化待到数字规律,要求学生仔细观察规律,主要考查同学们的抽象思维和逻辑推理的能力.

3.2 等比规律

例3.2.1 (2016 广东省中考第21 题)如图3,Rt∆ABC中,∠B= 30°,∠ACB= 90°,CD⊥AB交AB于D,以CD为较短的直角边向∆CDB的 同 侧 作Rt∆DEC, 满 足∠E= 30°,∠DCE= 90°,再用同样的方法作Rt∆FGC,∠FCG= 90°, 继续用同样的方法作Rt∆HCI, ∠HCI=90°,若AC=a,求CI的长.

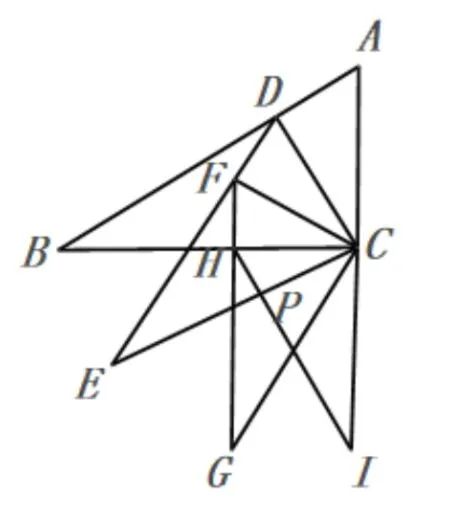
图3

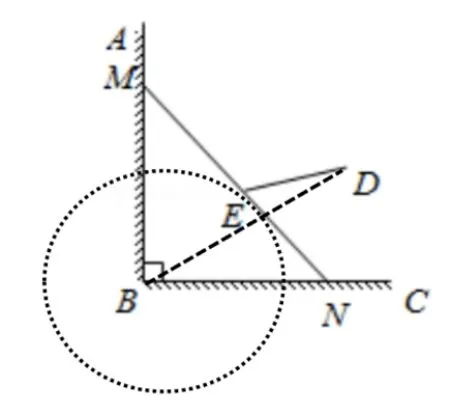
图4

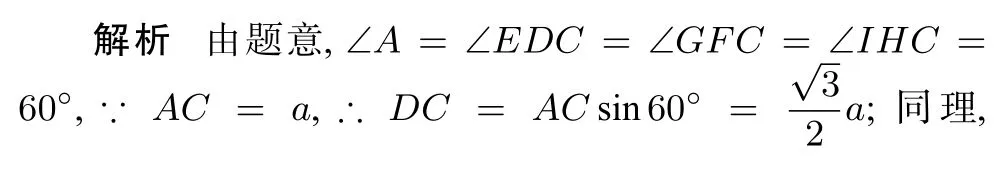
点评 该类题型在近几年中考经常出现,如2018 年广东省中考第16 题反比例函数与等边三角形规律问题,此类题型重在发展学生的符号意识,理解、运用符号表示数、数量关系和变化规律,使用符号可以进行运算和推理,得到的结论具有一般性.

4 条件推理题

条件推理题就是将题目中给出的已知条件进行一些变形,挖掘题干中隐含的条件,从而为成功解题做好准备.此类题型中题干所给的条件一般都比较简单,因此如何能够从中发现有用的条件就是解题的关键,特别是隐性条件推理题型是近年中考的重要考查方向[4].

4.1 隐性条件推理题

例4.1.1 (2020 年广东省中考第17 题) 有一架竖直靠在直角墙面的梯子正在下滑, 一只猫紧紧盯住位于梯子正中间的老鼠, 等待与老鼠距离最小时扑捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点, 模型如图,∠ABC= 90°,点M,N分别在射线BA,BC上,MN长度始终保持不变,MN= 4,E为MN的中点, 点D到BA,BC的距离分别为4 和2.在此滑动过程中,猫与老鼠的距离DE的最小值为____.

点评 隐性条件的代数推理题是中考的难点, 和近年考查热点“隐圆”能力要求类似, 要求学生构造解题模型,特别是2023 年广东省中考第23 题体现更加明显.此类题型解题关键在于梯子下滑过程中MN= 4 不变,即点E到点B距离保持不变,因此可确定点E在⊙B上运动,构造出“一箭穿心”模型,解决线段最值问题.

5 综合推理题

5.1 纯二次函数推理题

例5.1.1 (2023 广州中考第24 题) 点P(m,n) 在函数的图象上.

(1)若m=-2,求n的值;

(2)抛物线y=(x-m)(x-n)与x轴交于M,N(M在N的左边),与y轴交于点G,记抛物线的顶点为E.

①m为何值时,点E到达最高处;

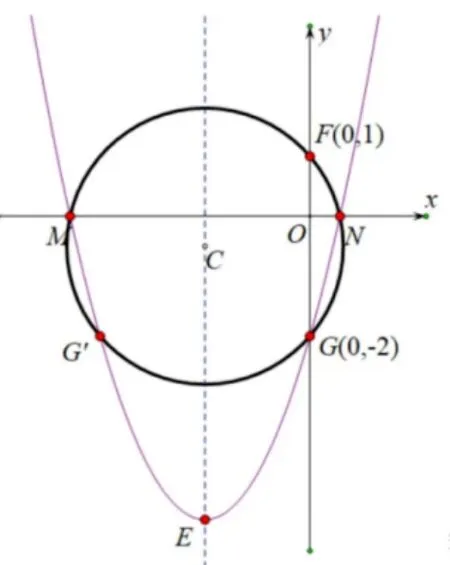
②设∆GMN的外接圆圆心为C,圆C与y轴的另一个交点为F,当m+n ̸=0 时,是否存在四边形FGEC为平行四边形? 若存在,求此时顶点E的坐标;如不存在,请说明理由.

解析 (1)n=-1;

(2) ①如图5, 不妨设M(m,0),N(n,0), 其中m

图5

点评 二次函数在初中数学课程占有重要比例,同时也是与高中数学知识衔接的重要部分.类似无图二次函数压轴题,在广州、深圳等地较为流行,本题主要考查了二次函数的综合应用,涉及到二次函数,考查了平行四边形的存在性问题,分类讨论是解题关键,体现新中考背景下数学抽象思维、代数推理能力的要求.

在初中数学人教版教材中, 代数推理贯穿始终,既存在于规律性问题的代数纯理论证明, 也存在在几何图形特点的代数证明.近年来广东省中考数学加强了对代数推理及相关知识点的考查,由于现在更加注重对初高中数学思维和解题方式的衔接,题型也更加创新和灵活,代数推理是一项需要长期培养的能力,需要教师在一线课堂教学中对学生持续引导和渗透.