一道解析几何模拟题的命制过程与反思*

广州市第四中学(510170) 刘运科

1 问题的来源

在“2023 年广东省普通高中课程教学改革学科组长示范培训”活动的一次讲座上,华东师大鲍建生教授提到一个“骑自行车趣题”: 一辆自行车的前、后轮在一个椭圆上,当自行车沿椭圆骑行一周时,前后轮与地面接触点的连线(假设长度为a)所扫过的面积是多少? 鲍建生教授对此问题的分析在此不表,笔者关注的是如何将此问题改编成高考模拟题.

2 利用GeoGebra 改编

这个问题的数学情境,是椭圆的定长的动弦扫过的面积.利用GeoGebra 作图,可以发现: 当弦长较小时,动弦扫过的图形看上去像是一个椭圆环(下左图);当弦长较大时,动弦扫过的图形比较怪异(下右图).如果直接考查动弦扫过的面积,显然要求过高;可以降低要求,只考查动弦上的一个点(如,中点)的轨迹.由此,得到一个新的数学问题: 求椭圆的定长动弦的中点的轨迹.

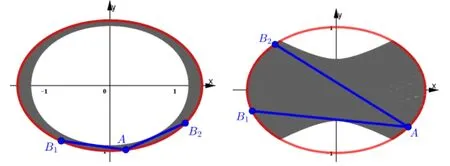
3 加工

4 再加工

如果仅仅求轨迹,考查的内容太少,对于能力弱的考生,又太难,对于能力强的考生,作为压轴题难度又不够,有必要前后各设计一个问题.为此,增加第一问: 已知椭圆的离心率为,短轴长为2,求椭圆的方程.最后一问考查什么好呢?笔者陷入了沉思.长度已经考查了,可以考虑考查面积;但是,求得的曲线不是常见的曲线,高中生无法求出曲线围成的面积.利用GeoGebra 作图,观察发现曲线恰在两个圆的外部,就计出了第三问: 证明曲线围成的面积大于(两圆的面积之和恰为).完整试题如下:

例1 已知椭圆E的焦点在x轴上,离心率为,短轴长为2.

(Ⅰ)求椭圆E的方程;

(Ⅱ)设AB是椭圆E的弦,且|AB| = 2,当AB在椭圆E上运动时,

(i)求AB的中点M的轨迹方程;

(ii)设点M的轨迹所围成的封闭图形的面积为S,证明:

5 制定前两问答案

(i)设A(x1,y1),B(x2,y2),M(x0,y0).

①当直线AB的斜率不存在时,注意到弦长恰等于短轴长,显然点M的坐标为M(0,0).

综上,点M的轨迹方程为x4+6x2y2+8y4-4y2=0.

6 研讨曲线的特征

笔者把题目也同时发给了科组几位青年教师,请大家做一做此题,再进行交流,经过各自独立研究30 分钟后,大家纷纷发表看法.

老师A:如果不借助电脑软件, 基本上不可能作出方程x4+6x2y2+8y4-4y2= 0 所表示的曲线, 更不可能求出其围成的封闭图形的面积.我一开始猜想图形可能是椭圆,用GeoGebra 作图后,发现图形好像是两个椭圆.学生想不出图形,也不会椭圆的面积公式,这一问超出了高中的知识范围.

7 研制第三问答案

8.试题评析与反思

根据课程标准的试题评价框架与水平划分[1],本题的试题评析表如下:

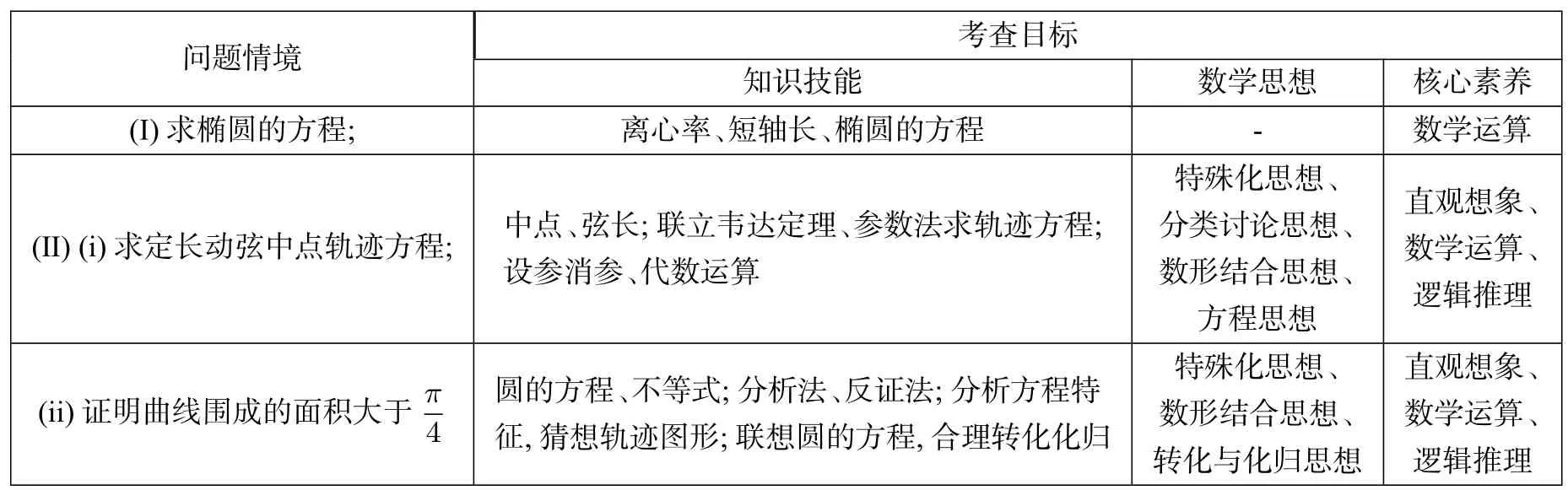
考查目标________________________________问题情境知识技能数学思想核心素养__(Ⅰ)求椭圆的方程;离心率、短轴长、椭圆的方程-数学运算__(Ⅱ)(i)求定长动弦中点轨迹方程;中点、弦长;联立韦达定理、参数法求轨迹方程;设参消参、代数运算特殊化思想、分类讨论思想、数形结合思想、______________________________________________________________________________________________________________________________________________________________________________________方程思想直观想象、数学运算、逻辑推理(ii)证明曲线围成的面积大于π 4圆的方程、不等式;分析法、反证法;分析方程特征,猜想轨迹图形;联想圆的方程,合理转化化归特殊化思想、数形结合思想、________________________________________________________________________________________________________________________________________________________________转化与化归思想直观想象、数学运算、逻辑推理__

从问题情境来看,本题以“数学情境”为命题载体,有“源于现实,暗合课本”的特点.问题源于“现实情境”——骑自行车问题,改编后与教材遥相呼应: 求动点的轨迹方程是教材中很典型的问题;探究不熟悉的曲线的性质,教材也给出了一般研究策略.在人教A 版选择性必修第一册的“3.1.2 椭圆的简单几何性质”[2]这一节中,教材指出,“通过对曲线的范围、对称性及特殊点的讨论,可以从整体上把握曲线的形状、大小和位置”.第三问的参考答案,正是按教材给出的研究策略得出的.

从考查目标来看, 本题前两问主要考查了从代数角度研究几何问题的基本方法——“坐标法”,这也是解析几何的基本方法.本题第三问, 命题视角聚焦在方程、曲线、不等式等知识的交汇点上,需要通过“分析——猜想——联想——转化——反证”的策略来求解.本题考查了数形结合、特殊化、分类讨论、方程、转化与化归等数学思想;考查了直观想象、数学运算、逻辑推理等核心素养.

反思:

(1)素养导向,技术助力,颇具新意.

本题形式常规而内涵丰富,探究味道浓厚,体现了素养导向.本题文字平实,易于理解,前半部分考查了解析几何的基本方法和思想,后半部分要经历层层递进的探究,解法看似在意料之外,实则在情理之中,体现了素养导向的试题特点.另外,利用GeoGebra 动态演示问题,获得猜想,从而命制出本题,GeoGebra 是一个重要的数学探究工具[3].

(2)难度偏大,未经检验,有待打磨.

虽然本题是压轴题,但难度偏大.主要是两个方面较难:一是求轨迹方程的代数运算较为复杂,消参的难度较大;其次是第三问的思维过于跳跃、发散,证明方法单一,如果改为证明曲线的纵、横坐标的取值范围,则可以使得考查目标更为聚焦,方法也会更加多样.另外,本题暂未在考试中使用,没有通过实践的检验,本题尚需进一步打磨完善.