指向核心素养以“学”为主的课例探究

董丽娥

《义务教育数学课程标准》（2022年版）（以下简称“新课标”）指出：要确定核心素养导向的课程目标，课程目标应以学生发展为本，以核心素养为导向，进一步强调让学生获得数学基础知识、基本技能、基本思想和基本活动经验，发展运用数学知识与方法，发现、提出、分析和解决问题的能力.指向核心素养以“學”为主的教学设计立足于新的课程理念，通过结构化的内容设计，围绕核心素养把课堂教学设计从以教师为中心的对话课堂向以学生为中心的任务课堂转变，将“四基”“四能”的培养融于学习活动中，使学生在任务的驱动下主动学习，发展核心素养.在此，笔者以“一次函数图象与性质”为例设计教学，将学生的行为表现与培养核心素养相关联，通过以“教”为主的课堂向以“学”为主的课堂的转变，探索指向核心素养以“学”为主的教学路径，促使学生自主学习.

一、内容和内容解析

1.教学内容：一次函数的图象和性质.

2.内容解析：人教版数学教材八年级下册第十九章“一次函数图象与性质”是在教学一次函数概念的基础上，研究其图象和性质的.这一内容与正比例函数一样，教师可以通过“画图象-观察图象-解释变量（坐标）意义”的步骤带领学生发现一次函数的性质.“以形表示数，以数解释形”的步骤和思想在今后其他函数的教学中依然有用.因此，在探究过程中，教师需要让学生通过画图、观察、猜想、类比、讨论等学习活动，经历“具体-抽象-具体”的学习过程，养成用整体的、联系的、发展的眼光看问题的习惯，培养数学抽象素养、数学建模素养，进而提升学生的归纳、系统的思维能力.研究一次函数的图象和性质，重点是让学生概括当k>0和k<0时，一次函数y=kx+b图象的特征，随着自变量x的变化，函数值y怎样变化.一次函数性质的核心是其增减性与系数k的符号之间的关系.本节课的教学重点：用数形结合思想，通过画图观察，概括一次函数的性质（函数增减性与系数k的符号之间的关系）.

二、目标和目标解析

1.学情分析

学生通过学习正比例函数，获得了对一类具体函数的数形结合的探究经验，用“描点法”画函数图象研究函数的性质，是直观认识函数性质的基本方法.一次函数的表达式比正比例函数多了一个常数b，函数图象受到k与b的共同影响.类比探究正比例函数图象与性质的过程，有利于学生掌握研究一类函数的一般方法.

2.核心素养目标解析

（1）学生经历用“描点法”画一次函数图象的过程，通过观察发现“一次函数的图象是一条直线”的学习活动，进而利用“两点法”画出一次函数的图象，并获得画函数图象的经验，发展学生几何直观素养.

（2）学生通过类比观察正比例函数与一次函数的关系，知道一次函数y=kx+b（k≠0）的图象可由正比例函数y=kx（k≠0）平移得到，能由正比例函数的图象和性质推断出一次函数的图象和性质，发展学生的推理能力及模型观念.

（3）学生通过所作图象观察当k>0和k<0时一次函数图象y=kx+b（k≠0）的变化情况，从而理解一次函数的增减性，同时以坐标为中介，把函数图象特征解释成变量的对应关系和变化规律，体会数形结合思想，培养学生的抽象能力和推理能力.

三、以“学”为主的课堂教学实践与分析

1.围绕素养目标设计学习活动

活动1：回顾旧知，提出问题，明确学习任务.

问题1：什么是一次函数？请写出三个一次函数的解析式.

设计意图：开放性地先让学生写几个简单的一次函数解析式，既为了帮助学生回顾一次函数的概念，也为了后面研究函数性质提供具体函数（最好与教材中的函数不同）.这样可以避免出现学生只看教材依样画葫芦的情况，如提供函数y=-2x+3.

问题2：前面我们学习了正比例函数，正比例函数有哪些性质？是怎样得到这些性质的？

设计意图：回顾正比例函数的研究方法，为在研究一次函数图象和性质时进行类比提供参照对象.

问题3：从解析式看，正比例函数与一次函数有什么关系？针对一次函数y=kx+b（k≠0），大家想研究什么？应该怎样研究？

设计意图：通过观察、回顾和比较正比例函数的研究过程，教师引导学生自然合理地提出一次函数的研究任务和研究方法.

新课标指出：要确定核心素养导向的课程目标.核心素养的核心是真实性，素养就是指能在真实情境中解决问题.因此，在课堂教学中，要将课堂教学设计从以教师为中心的对话课堂向以学生为中心的任务课堂转变，将“四基”“四能”的培养融于学习活动中.学生在学习任务的驱动下主动学习，发展核心素养.活动1以问题为支架，层层递进，指向学习目标.教师在活动过程中组织学生学习，通过指令引导学生开展自主学习.

活动2：动手实践，任务驱动，开展自主学习.

任务一：用“描点法”在同一直角坐标系画函数y=-2x与y=-2x+3的图象.

设计意图：根据研究步骤，教师引导学生先用“描点法”画一次函数的图象.

问题：观察这两个函数的图象的形状，说出它们之间的区别与联系.

设计意图：这个问题问域比较大，可回答的内容较多.学生的回答只要合理就应给予肯定与鼓励.如通过观察猜想函数y=-2x+3的图象可能是一条直线;函数y=-2x+3与y=-2x的位置关系是平行的，它们可通过平移得到彼此;两条直线的倾斜程度一样;观察得到它们与x轴、y轴的交点坐标等.在学生独立探究的过程中，教师巡视，对学生实施及时评价与指导.在学生得出结论之后，教师再进一步利用几何画板进行演示，确定函数y=-2x+3的图象是一条直线.教师利用几何画板动态演示两条直线的位置关系，能培养学生的推理能力和几何直观素养.

任务二：用你认为最简单的方法画出下列函数的图象：（1）y=-2x-1;（2）y=0.5x+1.

设计意图：结合“两点确定一条直线”的基本事实，教师引导学生自然、合理地发现可用“两点法”简便地画出一次函数图象.在取两点的时候，教师让学生自己总结后再与同伴交流，最终发现画出图象最简便的方法是找出图象与x轴、y轴的交点坐标.

活动2围绕学习目标设计了两项学习任务.在这两项任务中，学生主要进行自主学习，独立画图，经历“描点法”画一次函数图象到“两点法”画一次函数图象的探究过程，在两个学习任务里，教师根据学生的完成情况适时提出问题，要求学生独立解答.接着，教师进行评价，通过讨论得出结论.

活动3：动手实践，深入探索，合作交流学习.

任务一：在同一坐标系中画出下列一次函数的图象：

（1）y=x+1;（2）y=2x+1;（3）y=-x+1;（4）y=-2x+1.

问题：（独立观察）类比正比例函数，你能看出当k的符号变化时，函数的增减性怎样变化吗？

设计意图：通过类比正比例函数图象性质的研究方法，教师引导学生先画出若干个一次函数的图象，同时巩固“两点法”画一次函数图象.在对函数增减性的探究过程中，教师让学生先独立思考，之后小组交流得出结论，培养学生的抽象能力和模型意识.

任务二：及时巩固，解决问题，展示成果.

1.一次函数y=kx+b，y随x的增大而减小，b>0，则它的图象经过第           象限.

2.直线y=2x-3与x轴交点的坐标为           ;与y轴交点的坐标为           ;图象经过           象限，y随x的增大而           .

设计意图：及时巩固一次函数的图象和性质，培养学生的应用意识.学生独立完成任务之后各小组派代表展示，交流巩固.

任务三：思维导图小结，构建知识网络.

设计以下问题，并进行总结：

问题1：一次函数y=kx+b（k≠0）的图象是什么形状的？怎样用简便方法画出一个一次函数的图象？

问题2：一次函数有哪些性质？一次函数与正比例函数有什么关系？

问题3：我们是怎样对一次函数的性质进行研究的？

设计意图：教师引导学生在回顾课堂经历的基础上，从知识、方法的角度绘制思维导图，构建知识网.

学习活动3共设计了三个学习任务.任务一：学生利用“两点法”熟练画出函数图象，通过观察、比较得出一次函数的增减性，独立完成画图后，与同学交流观察所得性质.教师在这个过程中观察学生的独立学习及合作学习过程，在学生得出性质后利用几何画板直观动态演示，让学生通过视觉感知语言表征，进一步理解系数k对一次函数y=kx+b（k≠0）的增减性的影响.任务二：学生进一步巩固所得性质，学会迁移知识解决一些实际问题.在这个环节中，学生独立完成任务之后上台讲解，展示学习成果.任务三是这堂课的小结，教师通过问题引导学生构建知识框架，绘制知识网络图.

2.目标层级要求及目标检测

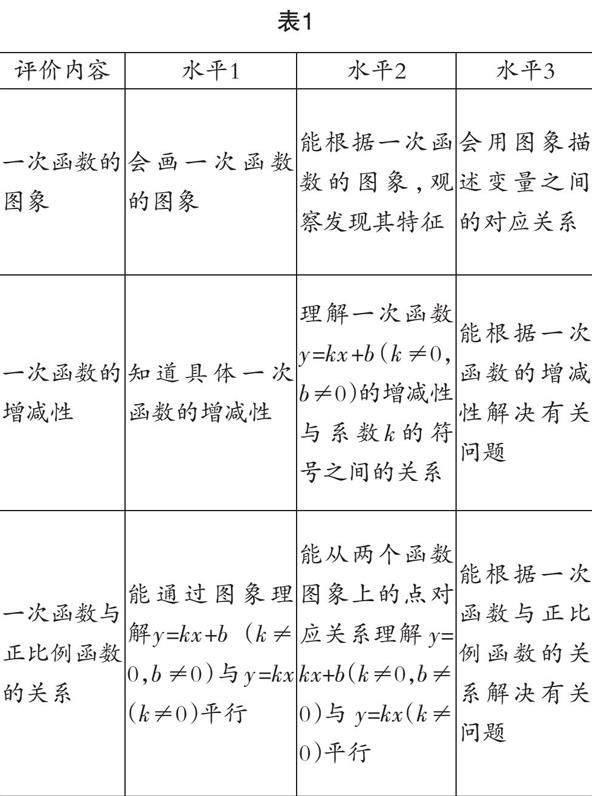
教师可将知识内容分解，把外在可观察的表现水平分级制作学习评价表（如表1），按照表格层级分层设计课堂作业，依据水平层级标注星级，水平层级从1到3，对应一星、二星、三星三个级别.

任务一：目标检测.

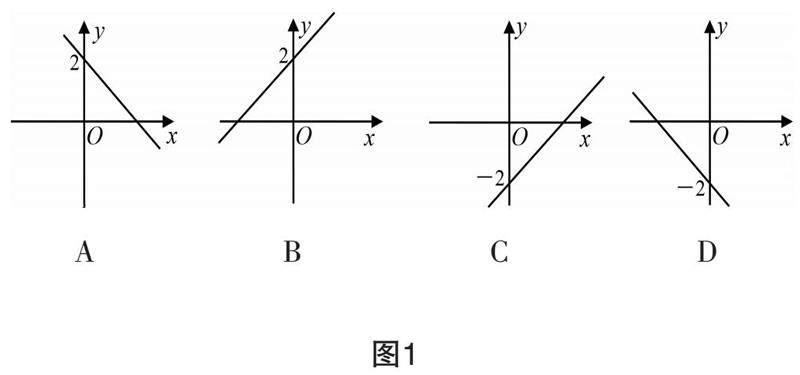
1.（☆）在图1中，一次函数y=x-2的大致图象为（ ）

A      B      C      D

2.（☆☆）下列函数中，y的值随x的值增大而增大的函数是（ ）

A.y=-2x  B.y=-2x+1  C.y=x-2  D.y=-x-2

3.（☆☆）直线y=2x-3与x轴交点的坐标为           ，与y轴交点的坐标为           ，图象经过第           象限，y随x的增大而           .

4.（☆☆）若直线y=kx+2与y=3x-1平行，则k=           .

5.（☆☆☆）P1（x1，y1），P2（x2，y2）是一次函数y=-0.5x+3图象上的两点，下列判断中，正确的是（ ）

A.y1>y2         B.y1

C.当x1y2

设计意图：教师设计层级清晰的课堂诊断作业，在学生完成检测后当堂批改.教师面批，学生互批.最后，师生对诊断结果进行评价，评价采取学生之间互评与教师评价相结合的方式.

任务二：对照目标层级，布置课后作业.

教科书第99～100页习题19.2第4，5，9，12，14题.

四、教学反思

1.以“学习任务单”为支架，任务驱动学习

本课例以学生的“学”为中心，以“学习任务单”为载体贯穿整个课堂教学.任务驱动学生主动思考、积极探索，合作交流.教师在课堂中主要负责组织学习活动，评价与指导学习，将学生引向深度学习.课堂上，教师引导学生完成建立新旧知识联系的复习任务，动手画图，类比正比例函数并发现一次函数的图象特征.通过独立思考、同伴交流，学生总结提炼出一次函数图象的性质.这些以学生为主体的学习活动带给学生的过程性体验会加深他们对数形结合思想的理解，加深他们对知识所蕴含的数学思想和数学方法的理解，也增强了他们应用数形结合思想解决问题的意识和能力.

2.注重教学内容与核心素养的关联

指向核心素养的以“学”为主的课堂教学，强调学生学习的主体地位，将教师的课堂行为定位为支持与促进.在学习活动设计的过程中，重视通过学习资源与学习任务促进学习真实发生.学生主要依靠自主學习达成目标.因此，在学习内容的设计上，教师将核心素养融入内容中，层层递进，通过画函数图象培养学生的几何直观素养和创新意识，在类比正比例函数的图象和性质的过程中培养学生的抽象能力、推理能力，最后形成模型观念，培养应用意识.

3.遵循知识逻辑，发展核心素养

在“一次函数的图象与性质”这节课中，“画图象-观察图象-解释变量（坐标）意义”这一研究函数图象性质的路径，需要学生动手操作，积极思考，从“描点法”到“两点法”绘制一次函数的图象，从观察正比例函数图象与一次函数图象之间的区别及联系，到总结得出一次函数的图象与性质，都用到了类比、分类讨论、数形结合的思想.学生在不断完成学习任务的过程中感悟数学思想，积累活动经验，掌握思维方法.这正是发展数学核心素养的有效路径.