“两位数加两位数”教学设计
文| 徐大莉
一、教学内容
人教版小学数学二年级上册第14~16 页“两位数加两位数”的进位加法。
二、教学目标
1.能够通过动手操作和自主探索理解两位数加两位数进位加法的算理,掌握笔算进位加法的计算方法,并能够准确地进行计算。同时,能够运用所学知识解决有关的实际问题。
2.通过编题、分类、反向思考、拓展延伸等多样化的教学活动,发展推理意识和思维能力,提高运算能力和解决问题的能力。
3.在学习过程中体验数学的趣味性和实用性,增强对数学学习的兴趣和自信心。同时,培养合作交流能力和创新意识。
三、教学重难点
教学重点:
掌握两位数加两位数进位加法的计算方法,特别要理解进位的产生和传递过程。
教学难点:
理解两位数加两位数进位加法的算理,体会从个位加起的必要性。
四、教学过程
(一)复习体验,衔接新旧知识
师:在学习新知识之前,我想先带大家回顾一下之前学过的一些内容,为我们新的学习之旅做好铺垫。
师:我们现在来进行一组口算练习,看看大家是否还记得“整十数加两位数”的计算方法。请大家看黑板,我们一起完成这些题目:24+20,10+34,30+27,19+70,54+40…
(口算过程中,学生纷纷给出答案,表现出对旧知识的熟悉和掌握。)
师:很好,看来大家都还记得怎么计算。
(设计意图:通过复习“整十数加两位数”的知识,为新知识的引入和学习做铺垫。教师在教学中积极引导学生将新旧知识相互衔接,让学生在轻松、愉快的口算练习中初步体验知识之间的联系,从而更好地接受和掌握新知识。)
(二)自主体验,促进知识习得
师:同学们,今天我们要继续探索数学的奥秘。在学习数学的旅程中,你们是探险家,而我是你们的向导。我们一起合作,发现两位数加两位数的秘密,好吗?
生:好!
师:请你们快速告诉老师,刚才我们做的属于什么加法?
生:两位数加整十数!
师:很好。但除了两位数加整十数,我们还能想到其他类型的两位数加法吗?
生:还有两位数加两位数?
师(鼓励):对。现在,我想请你们每个人都编一个两位数加两位数的题目,得数要超过100 哦。
学生纷纷编题,并在小组内交流。
师(走到学生中间,倾听):我听到了很多有趣的题目。你们真的很棒!现在,请你们在小组内讨论一下,这些题目该怎么算呢?
学生在小组内热烈讨论,并尝试计算。
师(引导):我看到很多小组都有了答案,谁能来分享一下你们的计算方法?
生(自信地):我们小组是这样算的,先加个位,再加十位,如果个位相加得数超过10,就把进位加到十位上。
师(赞赏):这位同学总结得很好,这就是我们今天要学习的两位数加两位数的计算方法。
师(进一步引导):现在,我们来看看这些题目。(呈现部分学生刚刚编的题目)如果给它们分类,你们觉得可以怎么分呢?
生:可以分为进位加法和不进位加法!
师(鼓掌):这位同学真的很聪明!那么,现在请男生编一些进位加法的题目,女生编一些不进位加法的题目,然后我们来交换解答,看看谁能更快、更准确地完成。
学生兴奋地编题、交换解答。
师(总结):前面我们一起探索了两位数加两位数的计算方法,你们不仅掌握了方法,还学会了如何编题。真的很棒!回家后,请大家再编一些题目,并尝试解答,明天我们来分享。
(设计意图:通过学生编题和分类体验的方式,引导学生深入探索两位数加两位数的计算方法。在这个过程中,学生不仅能够理解并掌握进位与不进位加法的规则,还能提升快速、准确编题的能力。)
(三)深入体验,促进思维发展
1.反向思考,突破难点
师:同学们,现在我们要进行第三轮编题挑战。这次的题目是:编出得数是60 多的两位数加两位数进位加法的题目。这次的要求比前两轮更高了,因为得数要超过60,还要考虑是进位还是不进位的情况。
学生尝试编题。
(展示学生的编题,并引导分析。)
师:我们来看看这些题目。22+27,十位相加是20+20=40,达不到60 多;30+34 虽然是60 多,但它是不进位加法;57+4 虽然结果接近60,但它不符合两位数加两位数的要求。
生:看来,编题不仅要考虑得数,还要考虑加数的位数和进位情况。
师:那么,要编出符合要求的题目,我们应该怎样思考呢?
学生思考后回答:如果编的是进位加法,那么十位相加的和加上进位的1 要等于60;如果是不进位加法,那么十位相加的和要直接等于60。
师(总结):很好,你们已经学会了反向思考。这种思考方式不仅可以帮助我们编出更符合要求的题目,还可以加深我们对两位数加两位数计算方法的理解。
2.拓展延伸,发展思维
师:经过前三轮的编题,我发现有些同学在编题时只关注了自己的想法,而没有考虑到其他可能性。比如,有的同学三次编题都是进位加法或都是不进位加法,这限制了我们的思维。现在,我来出一些题目,你们来判断这些题目的得数有没有可能是60 多?如果不可能,那结果可能是几十?
出示题目:24+27,28+35,54+2,54+7,46+1 等。
学生独立思考后回答:24+27 的得数不可能是60 多,因为即使个位相加满十向十位进1,十位相加也只有20+20=40;28+35 的得数是60 多,因为如果个位相加满十向十位进1,那么十位相加就有30+20=50,再加上进位的1 就是60,所以加数的个位之和要等于或超过10;54+2 的得数也不可能是60多……
师(总结与拓展):其实,我们还可以进一步思考这些题目的其他可能性。如果加数的个位之和等于或大于10,那么得数的十位就是加数十位之和加上1;如果加数的个位之和小于10,那么得数的十位就是加数十位之和。这些规律可以帮助我们更快速地计算两位数加两位数。
(设计意图:通过引导学生深入探索两位数加两位数的加法计算,达到促进学生思维发展的目的。利用反向思考,使学生不仅关注计算结果,还注重计算的过程和条件,从而帮助学生更好地理解两位数加法的进位和不进位规则。同时,鼓励学生进行批判性思考,发现并纠正自己在思考过程中存在的误区,突破学习难点。此外,通过具有挑战性的题目引导学生多角度思考和分析,拓展学生的思维广度,并提升计算的准确性和速度。)
(四)巧妙设计,让数学更贴近生活
师:同学们,看这里!(见表1)小玲去玩具店买了两个玩具,她给了店主一张50 元和两张10 元,并且店主还找回了一些钱给她。现在的问题是,小玲可能买了哪两种玩具?我们一起来找找答案吧!
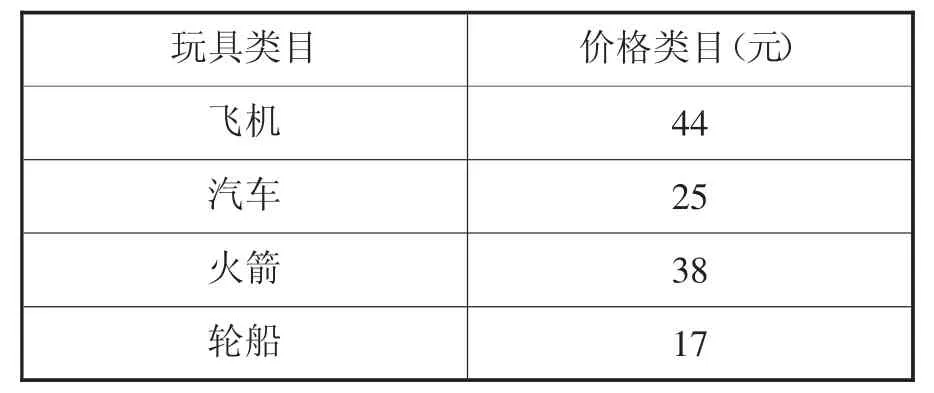
表1
(学生好奇地观察表中的玩具和相应价格。)
师:首先,我们来看看小玲付了多少钱。
生:一张50 元和两张10 元,一共是70 元!
师:很好!那么小玲买的两种玩具的总价应该是多少呢?
生:应该小于70 元,因为她还拿回了找零。
师:对!小于70 元,但也不能太低,毕竟她付了那么多。现在,我们来看看这些玩具的组合价格。有哪些组合是小于60 元的?
生:(开始计算各种组合的价格)飞机和汽车是69 元,太贵了!火箭和轮船是55 元,这个可以!
师:很好!火箭和轮船的组合是小于60 元的,那么小玲只需要付一张50 元和一张10 元就足够了。但题目说她付了70 元并且还有找零,所以这个组合不符合条件。
生:哦,我明白了!那她买的玩具组合的价格应该在60 元到70 元之间。
师:非常棒!现在你们来找找看,哪些组合的价格是在这个范围内的?
(学生开始以小组的形式计算并讨论各种可能组合。)
教师在学生讨论的过程中适时引导,鼓励他们多角度思考。
生:我找到了!飞机和轮船的组合是61 元,符合条件!
师:很好!还有其他组合吗?
生:汽车和火箭的组合是63 元,飞机和汽车的组合是69 元,也符合条件!
师:非常棒!你们不仅帮小玲找到了答案,还学会了如何运用数学知识解决实际问题。课堂即将结束,但学习永无止境,希望大家把今天学到的知识和方法应用到生活中,去发现更多的数学之美。下课!
(设计意图:本环节的核心在于通过贴近学生生活的购物情境,将抽象的两位数加法知识转化为具有实际应用价值的数学问题。其目的在于激发学生的探究欲望,促使学生主动运用所学知识去解决实际问题,从而加深对两位数加法运算规则的理解与掌握。在这一过程中,教师的作用在于引导和辅助,通过提出具有挑战性和开放性的问题——“小玲可能买了哪两种玩具”,鼓励学生进行多角度的思考,培养学生的逻辑思维能力和解决问题的能力。)
五、教学小结
本节课我主要围绕“两位数加两位数”的加法计算展开教学,通过设计不同层次的教学活动,帮助学生理解并掌握两位数加法的计算方法,同时提升学生的思维能力和解决实际问题的能力。首先,我通过复习体验环节,引导学生回顾了之前学过的“整十数加两位数”的知识,为新知识的引入和学习做好了铺垫。学生在口算练习中表现出对旧知识的熟悉和掌握程度,这也为接下来的教学顺畅过渡。
其次,在自主体验环节中,我鼓励学生自主编题并探索两位数加两位数进位加法的计算方法。通过小组讨论和分享,学生不仅掌握了进位与不进位加法的规则,还提升了编题和解题的能力。
在深入体验环节,我通过反向思考和拓展延伸的方式,引导学生深入探索两位数加法的计算方法和规律。学生在思考和分析过程中不仅突破了学习难点,还拓展了思维广度。这一环节有助于提升学生的思维能力和计算的准确性。
最后,在巧妙设计环节,我创设了一个贴近学生生活的购物情境,将抽象的数学知识转化为具有实际应用价值的数学问题。学生在解决实际问题的过程中巩固了所学知识,并学会了如何运用数学知识解决实际问题。这一环节的设计激发了学生学习数学的兴趣和动力。
总体来说,本节课的教学充分体现了学生的主体地位和教师的主导作用。然而,在教学过程中也存在一些不足之处,如部分学生在编题时思路受限、缺乏创新性等。针对这些问题,我会在后续的教学中加强引导和拓展,鼓励学生多角度思考,以使其更好地掌握数学知识和提升数学素养。

