新课标背景下促进“四基”与“四能”发展的措施研究

张晶

［摘  要］ “四基”与“四能”的培养是义务教育阶段数学课程教学的基本要求. 文章基于《义务教育数学课程标准（2022年版）》，以“直线与圆的位置关系”的教学为例，分别从“情境创设，发现问题”“揭露课题，引发探究”“概括抽象，理解新知”“数形结合，实现迁移”“例题训练，巩固新知”“回顾总结，设计作业”六个方面展开培养学生“四基”与“四能”的教学设计与教学分析.

［关键词］ “四基”；“四能”；新课标；教学

《义务教育数学课程标准（2022年版）》（下称“新课标”）再次强调数学教学要注重发展学生的“四基”“四能”. “四基”是指基础知识、基本技能、基本思想与基本活动经验，“四能”是指通过义务教育阶段的教学，让学生自主发现数学学科与生活以及其他学科之间的联系，提高发现问题、提出问题、分析问题与解决问题的能力. 这一目标凸显当代数学教育注重的是教学过程与能力的培养.

教学简录

1. 情境创设，发现问题

课堂伊始，教师借助PPT展示王维的《使至塞上》中所提及的长河落日图（如图1所示），引导学生感知诗中边塞的美丽景色.

师：大家都见过落日的美景，如图1所示，若将长河落日图转化成我们熟悉的数学几何图形，该怎么处理比较合适呢？

生1：若将图中的长河理解为一条直线，那么图中的落日则可视为一个圆.

师：很好！随着落日位置的变化，它们所转化成的几何图形之间的位置关系会发生怎样的变化？

设计意图数学本就源于生活，将诗歌中的情境作为背景，一方面凸显数学学习的趣味性，另一方面有效激发学生的探索欲，让学生从这个情境中发现问题，并在教师的点拨下做好提出问题的准备. 当然，诗歌中的图有着丰富的意境，这对发展学生的数学美感具有重要意义，学生从图中主动发现并提出问题，增强直观想象能力的同时熟悉其他学科与数学、生活与数学之间的联系.

基于情境背景，学生自主操作几何画板，呈现出长河落日的动态变化图，即圆与直线的位置关系（如图2）.

师：观察图2，我们发现圆和直线之间具有几种位置关系？具体是怎么分类的？

设计意图几何画板是重要的辅助工具，让学生亲自操作几何画板可深化学生的操作能力与探索兴趣，这也是促使学生主动发现并提出问题的基础.

2. 揭露课题，引发探究

探究活动1：要求学生在白纸上画一条直线，将一张圆形卡纸置于直线上方缓慢移动，探索直线和圆的不同位置关系.

探究活动2：将圆形卡纸固定在一张白纸上，并在这张白纸上画多条直线，观察圆形卡纸和不同直线之间存在怎样的位置关系.

基于活动要求，学生展开合作交流，随着探究活动的深入，学生自行分析圆和直线的位置关系，并展示成果.

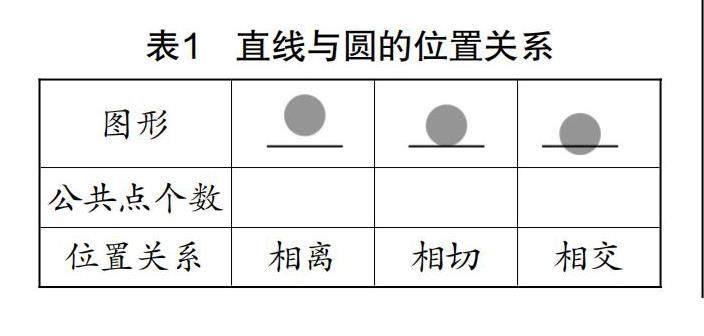
师：通过以上探索，大家发现直线与圆之间存在几种不同的位置关系？分类标准是什么？

生2：存在三种不同的位置关系，根据公共点的个数来分类.

师：很好，那