谈初中数学章引领课的设计思路与实施建议

［摘  要］ 近些年，各地积极倡导开展章引领课教学，章引领课对本章的教学起着“开山辟路”的作用. 文章对章引领课的“课前、课中、课后”三阶段的教学过程进行梳理，提出各阶段具有价值的研讨问题及对策，并对章引领课的作业进行思考与设计，形成章引领课教与学的闭环，切实发展数学能力，让学生“乐学、乐思、乐行”，发挥出章引领课更大的价值.

［关键词］ 章引领课；设计思路；作业设计；实施建议

基金项目：中央电化教育馆“‘人工智能+教育创新应用实践研究”的子项目“基于智慧学习空间支持的学科证据性思维素养提升研究”（教技资（2022）02-005号）；江苏省教育教学“十三五”规划2020年度重点课题“青年教师‘草根研修工作坊自主构建的实践研究”（B-b/2020/02/71）；南京市江北新区第十二期课题“新课标背景下初中数学结构化教学策略的实践研究”（KTGR20220094）.

作者简介：高凯亮（1995—），本科学历，中学二级教师，南京市浦口区杜育林名师工作室核心成员，南京市江北新区初中数学工作坊核心成员，从事初中数学教学与研究.

章引领课的含义及价值

章引领课，亦称章统领课、章起始课，是一章教学的第一节课. 《义务教育数学课程标准（2022年版）》（以下简称“新课标”）指出，在课程内容组织上，重点是对内容进行结构化整合，探索发展学生核心素养的路径［1］. 章引领课的定位是帮助学生从整体上把握学习内容，感悟数学知识的系统性、整体性；在知识的习得过程中了解知识的来龙去脉，为学生“再创造”知识提供有力载体，培养学生“会学、会想、会用”知识的能力，使得学生“乐学”，激发学生学习主观能动性. 下文将梳理章引领课中“课前准备阶段、课中实施过程与课后总结反思”三个阶段的主要流程，提出三个阶段中有价值的研讨问题及策略，并完善章引领课的作业设计，形成章引领课教与学的闭环.

章引领课的设计与实施

1. 课前准备阶段

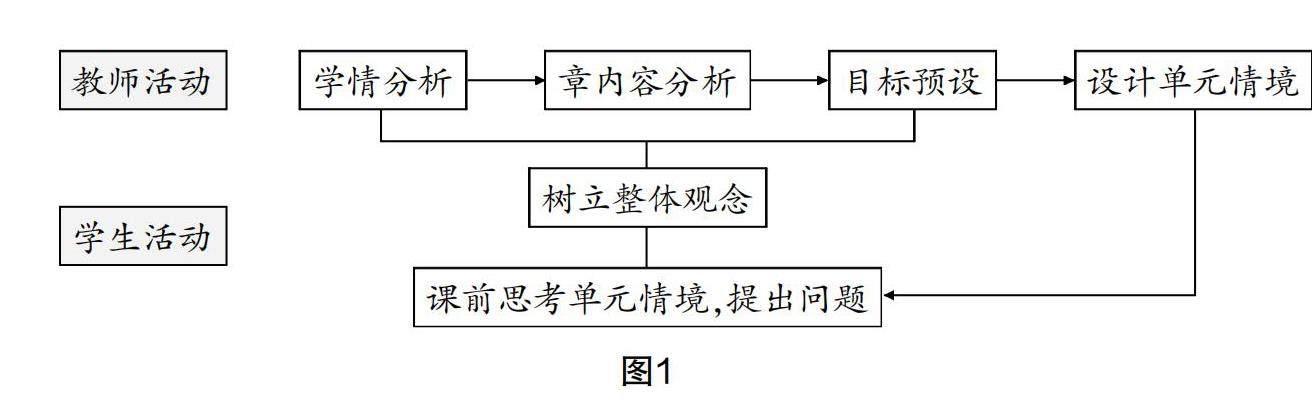
章引领课的课前准备与传统课时教学的课前准备类似，教师都需要从学情分析、教材分析、目标预设、教学过程等几方面做出准备，但章引领课的课前准备需要教师在学情分析、章内容分析环节更加深入，例如，本章的学习内容学生已经具备了哪些经验，必要时可追溯到小学阶段是如何学习此模块内容的，甚至可以延伸到高中对学生学习具有怎样的影响，对学生可持续发展具有怎样的引领作用. 目标预设需要注重知识之间的内在联系，需要做到“粗细结合”，其目的是帮助学生树立整体观念；若目标预设得过“粗”，则会太“虚”，课堂上的构架看似“高大上”，实际上对学生后续学习本章知识的引领作用会大打折扣；若目标预设得过“细”，则会变成一节高浓度知识点介绍课，不能激发学生深度思考，甚至违背了章引领课培养学生“会学、会想、会用”知识的初衷. 在目标预设的基础上，教师设计出具有引领作用的单元情境，并布置学生在课前根据单元情境提出问题，教师筛选出学生提出有价值的问题在课堂上进行研讨，并让学生分享是如何思考的，拟达到逐渐培养学生在具体情境中提出有价值的问题的能力，章引领课课前准备工作如图1.

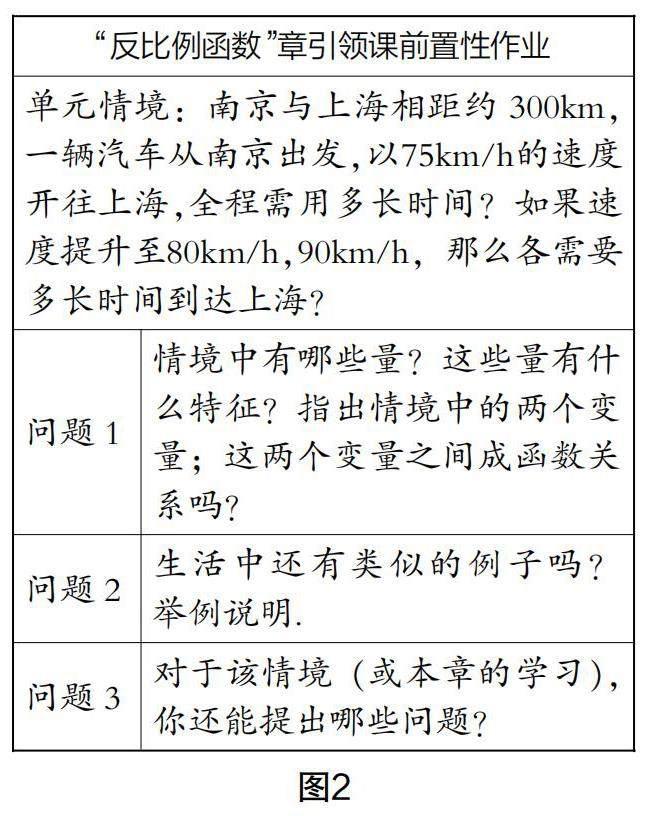
例如，苏科版教材“反比例函数”是继“一次函数”后研究的第二类初等函数，学生已经具备了研究相关知识的经验，但是由于小学教材没有涉及反比例关系，所以在“反比例函数”引领课中最好能够通过生活实例归纳、抽象出研究对象（反比例函数），让学生感知反比例关系过渡到反比例函数的过程，明確研究对象的由来；“反比例函数”章引领课可设置如下教学目标：（1）能在生活实例中归纳、抽象出反比例函数的定义，体会反比例函数是描述具有反比例变化规律的数学模型；（2）会判断两个变量是否成反比例函数关系；（3）类比一次函数的研究路径，构建出反比例函数的研究路径；（4）能根据反比例函数的解析式大致猜想出该函数图象的特征. 设计如下单元情境（图2）布置学生课前思考，并提出问题，教师根据学生提出有价值的问题进行后续教学.

2. 课中实施过程

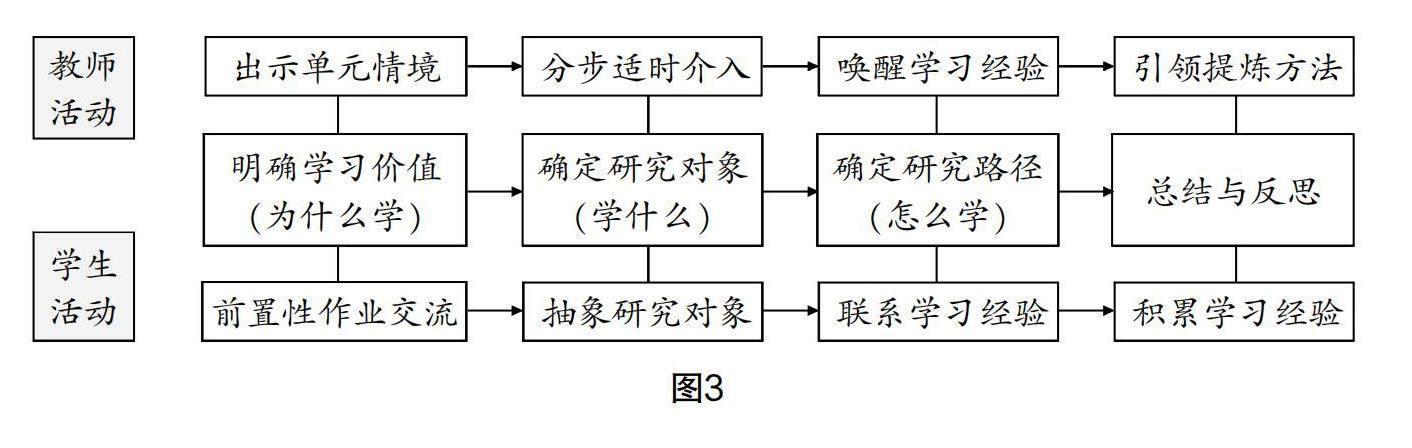
“新课标”指出，数学是源于对现实世界的抽象，通过数量和数量关系、图形和图形关系的抽象，得到数学研究对象，基于抽象结构，通过对研究对象的符号运算、形式推理、模型构建等，形成数学的结论和方法，帮助人们认识、理解和表达现实世界的本质、关系和规律［1］. 在单元情境（前置性作业）的驱动下，引领学生课前发现、提出有价值的研究问题，章引领课的教学中，首先需要帮助学生确立本章的研究对象，再从宏观视角确定本章的研究路径，最终形成研究一类问题的基本“套路”，即课堂实施过程中需要将问题聚焦到为什么学？学什么？怎么学？课堂上，在核心问题的引领下，促使课堂活动整体化，给学生更多思考的时间与展示的空间，充分发挥教师是组织者、合作者、引导者的角色，为学生“再创造”知识提供时间与空间；章引领课课中实施过程如图3.

例如，“反比例函数”章引领课实施过程中，首先出示前置性作业中的问题情境（图2），师生共同研讨问题1，其目的是先明确什么是反比例关系，再从函数视角认识反比例关系，通过问题2引领学生感悟生活中存在大量类似的实例（可投影学生前置性作业中列举的实例），归纳、抽象出研究对象（反比例函数），并引导学生用解析式对该函数进行定义；经历反比例关系到反比例函数的过程，感悟反比例函数的内涵，体会反比例函数是描述具有反比例变化规律的数学模型. 笔者在批阅学生的前置性作业时，发现学生虽然不能明确给出反比例关系的定义及反比例函数的名称，但学生能够列举出生活中大量类似的实例，在单元情境的引领下，让学生感受到生活中类似的例子有很多. 因此，在课前让大部分学生都能深刻体会到有必要建立一个模型（反比例函数）对此类问题展开研究，让学生在课前对本节课“为什么学？学什么？”有初步了解，让每一位学生都能深刻体会到数学源于对现实世界的抽象；但是建立模型的过程难度较大，大部分学生在课前无法独立完成，需要教师与学生在章引领课上共同完成.

接下来，根据之前研究一次函数的经验，从宏观视角对研究对象（反比例函数）建立研究路径（定义—图象—性质—应用），这便完成了章引领课中第三个阶段，即怎么学. 以单元情境中t=（v>0）为载体，试猜想该反比例函数图象的特征；由于实际问题中v>0，所以该函数图象仅会在第一象限且与t，v轴无交点；由于v值越大，t值越小，所以当v>0时，该函数图象呈下降趋势；教师便可继续追问：若v<0时，能猜到函数图象是怎样的吗？

最后，投影学生前置性作业中提出的问题，笔者在批阅学生的前置性作业时，发现大部分学生能够提出此类问题（若要汽车2 h内到达上海，那么速度至少是多少？），对于该问题，引导学生意识到要求出速度至少是多少，需要先求出一个范围，在范围中选取最小值；由于学生没有反比例函数的知识储备，可先引导学生将该问题转化为方程问题，再根据v与t的变化规律感受临界值的合理性；也可引导学生将该问题转化为解分式不等式，在去分母时要特别注意引导学生进行分类讨论，章引领课上教师可以不给出该问题的规范解答过程，这是后续需要系统研究的一类实际问题. 该问题速度的临界值是150 km/h，但是实际上高速公路最高速度为120 km/h，说明2 h到达上海不切实际，让学生意识到解决问题后，还需要慎重考虑是否符合实际，培养学生养成严谨的科学态度与理性精神. 事实上，这也是培养学生养成事后总结与反思的好习惯. 课堂小结中，教师再引领学生回顾研究对象的由来，从宏观视角梳理数学对象的研究路径，帮助学生直接积累研究一类问题的活动经验.

3. 课后总结反思

课后作业是检测课堂效果的有效途径之一，“新课标”指出，需要注重实现“教—学—评”一致性，章引领课的作业设计也不例外，作业设计中还需要注重以下四个方面：第一，基础性，章引领课是本章的第一节课，设计的作业不宜过难，否则会打击学生学习本章内容的积极性，产生负面影响. 第二，生长性，章引领课的作业中不能“就题论题”，学生对问题的思考需要具有动态性、阶段性［2］. 例如，反比例函数章引领课上，学生只经历了“由数想形”的猜想，究竟猜想得对不对还有待考证，由于学生已经具备了画一次函数图象的经验，作业中可布置学生“画图验证”，本章第2课时“反比例函数的图象与性质”也将是章引领课作业的延续，通过第二课时的系统学习，学生对反比例函数图象的认识会更加深刻. 第三，层次性，例如，根据解析式的结构特征，能猜想出该函数具有怎样的对称性吗？能根据解析式进行解释吗？图象的形状是直线吗？由浅入深的作业设问能够激发学生深度思考. 第四，反思性，章引领课上的课堂小结是在教师的引领下完成的，过程较快，需要学生课后进行内化反思. 例如，反比例函数章引领课后，布置学生撰写本章（反比例函数）的研究框架及学习心得，即便是几句话的心得，也是学生对学习过程的梳理与活动经验的积累，培养学生总结反思的习惯非常重要，这对学生的自身发展起着至关重要的作用. 章引领课作业设计与总结反思的过程如图4.

实施建议

1. 处理好章引领课与章复习课的关系

章引领课上先抽象出本章研究对象，再对本章学习路径进行宏观构建，为后续微观研究该对象提供明确的方向，对本章的学习起着“开山辟路”的作用. 章复习课是对一章的学习内容、方法、经验的整体梳理. 如果章引领课是“头”，那么章复习课就是“尾”，教学中章引领课与章复习课同样重要，两种课型能够给学生积累不同的活動经验，教师在一章的教学中需要做到“有头有尾”. 在不同课型中对同一研究对象积累不同的活动经验，对学生后续学习相关内容会产生指引作用. 正如史宁中教授所说“一个人会不会想问题是经验的积累，会不会做事情是实践的结果”.

教学中要特别重视没有“类比源”的章引领课，笔者通过中国知网数据库以“章引领课”（或章统领课、单元教学）进行检索发现，有很多精彩的章引领课案例，例如，一元二次方程章引领课、图形的相似章引领课、平行四边形章引领课等. 显然，这些课例都有一个共同的特点，即有“类比源”，构建一元二次方程的学习路径可以类比一元一次方程的学习过程，包括上文构建反比例函数的学习路径是类比一次函数的学习过程，等等. 那么，没有“类比源”的章引领课如何进行？仔细分析教材后发现，初中阶段没有“类比源”的知识往往能够在小学找到它们的“影子”. 例如，“图形的平移”是苏科版教材七年级下册第七章“平面图形的认识（二）”中的内容，也是苏科版教材第一次系统研究的图形运动，系统研究“平移”会对“翻折、旋转”的学习产生重要影响. 实际上，该内容学生小学已经学习过，但小学的学习不系统，仅仅停留在感性认识层面，教师实施章引领课前可对该内容进行前测，通过前测数据进行分析，精准定位学生对该内容认识到哪个层次结构，再设计问题串引领学生将这种“感性认知”逐渐过渡到“理性思维”. 对于没有“类比源”的章引领课，教师更要注重学生已具有的学习经验与生活经验；学生对知识的理解具有阶段性，本章复习课上，教师切勿忽略引导学生从宏观与微观两个视角对“平移”进行系统梳理，并在章复习课后布置每一位学生进行总结并撰写学习随笔，其目的是为学生后续学习“翻折、旋转”建立“类比源”［3］.

2. 重视章引领课单元情境与课后作业设计

单元情境是依据本章的核心内容设计的情境，对本章的学习起着引领作用，单元情境应当具有“入口宽、开放性、真实性”的特点，其目的是给不同层次的学生更多的创造空间. 例如，上文中反比例函数章引领课的情境设计源于生活需要，是生活中存在的真实问题，并且课前布置每一位学生对该情境进行思考，笔者认为，章引领课上给予学生思考的时间有限，单元情境尽量给学生在课前进行思考，但需要在单元情境中设计能激发学生思考的问题串，让每一位学生尽可能地自主发现、抽象出研究对象，并提出有价值的研究问题，教师根据学生前置性作业的完成情况，对其精准制订教学活动.

课后作业不仅是检测课堂效果的途径，也是课堂学习过程的延续，需要处理好二者的关系. 例如，上文反比例函数章引领课中对反比例函数的图象仅有“由数想形”，作业中布置学生“画图验证”；根据一次函数的学习经验，反比例函数图象的形状也是直线吗？能说明理由吗？梳理反比例函数的研究路径等，这些问题都是课堂上学习的“续集”，目的是为学生“会学、会想、会用”提供更多机会.

3. 适当设计课堂游戏，提高章引领课效率

托尔斯泰曾说：“成功的教学所需要的不是强制，而是激发学生的兴趣.”让学生“愿意思考”是激发学生学习兴趣的前提条件，教学中设计适当的课堂游戏能够激发学习兴趣.例如，上文中反比例函数章引领课上对反比例函数图象“由数想形”，可将此活动名称改为“有理猜形”游戏 ，这里的“理”可以是根据反比例函数解析式的“结构”进行猜想，也可以是一次函数学习经验的类比迁移（反比例函数的图象也是直线吗？）等，学生每提出一个猜想后需要阐述提出这种猜想的理由，总之，猜想需要做到有“理”可循. 学生在课后“画图验证”的过程中，若发现自己课堂上的猜想是正确的，教师可为学生进行加分，累计到期末总评成绩中. 从课堂教学效果来看，设置此类课堂游戏，学生在阐述“理”时，全班学生的注意力会更加集中，这便是生生之间“无形”的交流；从评价体系来看，这也是多维评价方式的探索，鼓励学生自我监控学习的过程和结果.

结束语

总之，章引领课并非一章教学前的任务，而是要以章引领课为载体，让学生体会研究对象的由来，在数学化的过程中感悟数学本质，经历科学探究的步骤，培养学生形成实事求是的科学态度. 教师要在“课前、课中、课后”为学生尽量提供更多“会学、会想、会用”知识的载体，使得学生“乐学、乐思、乐行”，发挥出章引领课更大的价值.

参考文献：

［1］中华人民共和国教育部. 《义务教育数学课程标准（2022年版）》［M］. 北京：北京师范大学出版社，2022.

［2］阙成. 初中数学习题的重构与再设计［J］. 中学数学月刊，2022（11）：44-47.

［3］高凯亮. APOS理论背景下初中数学概念教与学——以蘇科版数学教材七下“图形的平移”为例［J］. 初中数学教与学，2022（20）：8-11.