数学文化的教育价值与渗透方法的研究
叶巧珍
[摘 要] 随着新课改的推进,数学文化越来越受到广大教育工作者的关注.文章认为数学文化具有利于学生理解数学本质、激发求知欲、发展核心素养等重要价值,并以“勾股定理”的教学为例,从“情境创设,激发兴趣,引出主题”“自主探究,启发思维,建构新知”“例题教学,变式拓展,加強应用”“归纳定理,提炼总结,巩固提升”四个环节具体谈谈渗透数学文化的措施.
[关键词] 数学文化;价值;勾股定理
《义务教育数学课程标准(2022年版)》(简称“新课标”)提出:课程内容是实现课程目标的载体,数学课程内容的选择应凸显学科特征,关注学科发展前沿与数学文化,引导学生继承并弘扬中华民族的优秀传统文化. 数学学科本身就是一种文化,既然为文化,就具备传承与发展的特性. 语言、宗教、文字等文化存在地域之分,但数学思想、方法、定理、数学史、数学美等却无地域之别.
数学文化的教育价值
1. 利于学生理解数学本质
数学是一种理性的认知模式与思维范式,从表面上看数学教学主要着重于定理、运算、法则、解题等方面的研究,而事实上,数学文化的渗透、思想方法的培养以及核心素养的发展才是数学教学的本质. 因此,教师应关注数学本质的教学,切忌为追求分数而忽略对学生数学思维、能力等的培养.
教学中,数学文化的介入能让学生从各个方面体验、感悟数学既是一门自然、语言、知识或与社会联系的工具,又是数学思想方法、审美艺术等的综合体. 尤其是在课堂中渗透数学文化,能让学生对知识之间的联系产生更加深刻的认识,为更好地认识数学本质奠定基础.
2. 利于学生激发求知欲
G. 波利亚曾提出这样的担忧:数学在基础学科中是最不得人心的. 确实,迄今为止,仍有不少人认为数学是一门抽象、枯燥、单调的学科,其实真正深入数学领域,会发现数学是一门充满生机与活力的学科,具有独特的魅力. 如哥德巴赫猜想、黎曼猜想等都是令人神往的问题,将这些问题有机地融合在课堂教学中,可让学生漫步于不断发展的数学文化长河,开阔视野、启发思维、激发求知欲,形成创新能力.
3. 利于学生发展核心素养
“新课标”引领下的数学教学以发展学生的核心素养为主要目标,数学文化的价值不仅体现在知识本身,还彰显在核心素养的发展上. 如今我们所接触到的数学内容,小到一个符号,大到知识体系,都经历了万千坎坷才逐渐完善而成. 揭示这些知识的形成与发展过程,能让学生从根本上认识知识的源头,重塑知识的“再发现”过程,为形成良好的数学抽象、数学建模、逻辑推理、直观想象等能力奠定基础,而这些能力又是组成核心素养的关键要素.
数学文化的渗透措施
1. 情境创设,激发兴趣,引出主题
教学情境是指教师为了更好地实施教学活动而营造的一种教学环境,是学生产生学习行为的基本条件. 情境创设需紧扣教学目标与学情,尽可能地接近学生的“最近发展区”,并通过多元化的方式提供丰富的信息,以便于学生更加直观地理解教学内容. 以数学史作为情境导入内容,能为课堂营造一种良好的文化氛围,激发学生的学习兴趣,推动学生的探索欲,为课堂教学奠定良好的情感基调.
“勾股定理”在数学学科中具有重要地位,为了激发学生的研究兴趣,教师可从史料着手,引出本节课的教学主题.
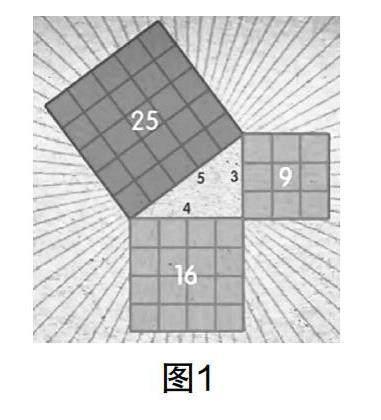
情境 某天,周公问商高:“咱们的祖先为我们留下了度量法,但很多东西我们也不能爬上去测量,也没有合适的测量标尺,你说说这些关于天地的数据是从哪儿来的. ”商高说:“数出于圆方,圆出于正方形,正方形出于矩形,矩形尺寸各异. 其中有一条原理,截出一个矩形一边长为3,一边长为4,对角线为5,沿着两边与对角线的外侧各作一个正方形,所得正方形的面积关系如图1所示. 这个原理是从大禹治水中得来的. ”
师:这是记载在《周髀算经》中的故事,可见咱们祖先在两千多年前就将“勾股定理的性质”应用到生活实际中,观察商高所描述的图形,该图的中间就是我们所熟悉的直角三角形,也是本节课探索的主题.
评注勾股定理被誉为“数学中的千古第一定理”,具有代数与几何的双重特征,是沟通几何与代数的桥梁. 勾股定理历史悠久、作用突出,对学生学习几何具有深远的影响,尤其是它的发现、发展、验证与应用等,都蕴含了丰富的数学文化,具有一定的教育价值. 因此,本节课以《周髀算经》中的故事作为情境导入的素材,能有效地激发学生的研究兴趣与民族自豪感.
2. 自主探究,启发思维,建构新知
“新课标”一再强调:学生才是课堂真正的主人,教师应在课堂上充分调动学生的感官系统,让学生在手脑并用中发挥自己的主观能动性,主动获得知识与技能. 因此,教师在课堂上应尽可能地创造更多的机会让学生动手操作、动眼观察、用脑思考,从批判性的角度建构新知. 本节课,笔者以问题驱动的方式,引导学生进入自主探究状态.
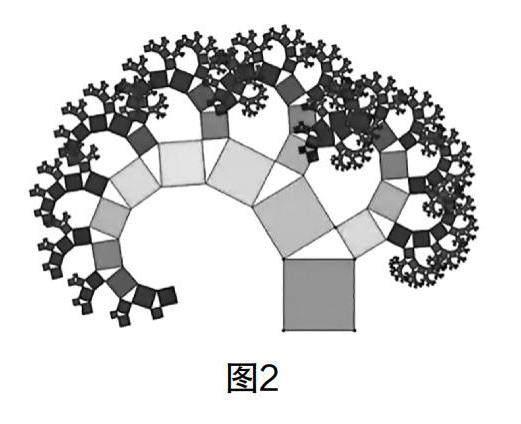
师:如图2所示,这是毕达哥拉斯树,俗称“勾股树”,它由著名的数学家毕达哥拉斯所画,大家觉得这棵树怎么样?
生(齐):好神奇,太美了!
师:确实很神奇,现在我们以小组合作学习的方式来进行如下探究.
探究1观察图3,填写表1,图中每个小正方形表示一个面积单位.
思考:通过对表格数据的观察,说说三个正方形的面积之间具有怎样的数量关系,直角三角形的三边长度之间又有怎样的关系.
学生经合作交流,初步获得结论:大正方形的面积等于两个小正方形的面积和;直角三角形斜边的平方等于两条直角边的平方和.
探究2以上结论是否适用于所有三角形呢?观察图4,重新填写表1,图中每个小格表示一个面积单位.
思考:分析图表数据,图4中正方形Ⅰ、正方形Ⅱ、正方形Ⅲ面积之间存在怎样的数量关系?直角三角形的三边长度之间又具有怎样的关系?
学生再次合作交流,获得猜想:假设a,b,c分别为一个直角三角形的两条直角边与斜边,那么该直角三角形的三边关系为a2+b2=c2.
探究3PPT展示在北京召开的第24届国际数学家大会的会徽,如图5所示,介绍会徽源自我国汉代的“赵爽弦图”.
如圖6所示,教师以“会徽”为背景,提炼出简图,要求学生根据要求探索简图中大、小正方形的面积关系,并获得相应的结论(过程略). 为了充分了解学生的思维状态,教师可加强巡视,并要求各组选派一名成员汇报组内讨论结果.
探究4基于以上“观察—猜想—验证”的过程,请大家用不同的方式概括勾股定理.
此环节不急于用文字描述定理,而是结合语言、公式的变形等,对定理形成一个全方位的认识. 教师在此处应给予学生更多的激励性评价,以唤醒学生深入探究的信心,让学生主动锤炼对勾股定理的表述,形成更加深刻的理解.
(合作交流,获得结论)
文字语言:直角三角形的两条直角边的平方和与斜边的平方相等.
符号语言:在Rt△ABC中,已知∠C为直角,BC,AC,AB边的长度分别为a,b,c,那么a2+b2=c2.
图形语言:如图7所示,由a2+b2=c2可推导出a=,b=,c=.
评注循序渐进的探究活动,由浅入深地启发了学生的思维. 学生从数学史的角度出发,通过自主探索与合作交流的方式对勾股定理的本质与内涵进行了猜想与验证,这种探索模式不仅强化了学生对勾股定理的认识,还有效地渗透了数学文化,培养了学生的数学审美能力,陶冶了学生的数学情操,从真正意义上激发了学生的学习兴趣,有效地推动了学生数学核心素养的形成与发展.
3. 例题教学,变式拓展,加强应用
波利亚认为:一位好的教师能利用有意义却又不复杂的例题去帮助学生挖掘知识的内涵,将学生带入一个新的完整的领域. 在例题教学过程中,“懂而不会”的现象非常普遍,因此例题的设计非常重要. 恰到好处的例题训练能及时帮助学生巩固新知,形成技能.
本节课,如何基于数学文化渗透的角度,围绕教学目标设计出“牵一发而动全身”的例题呢?根据学生在课堂中的反馈情况,教师可为学生量身打造出相应的例题,并通过变式拓展深化学生对公式的理解与应用,以建构完整的认知结构.
例题我国古代称直角三角形的短边为“勾”,用b表示;称较长的直角边为“股”,用a表示;称斜边为“弦”,用c表示,若勾三,股四,则弦几何?
设计意图通过对勾股的介绍,让学生感知中国数学文化的博大精深,以引导学生积极尝试与探索,强化学生对勾股定理的应用意识.
变式1请将图8中四个全等直角三角形拼搭成一大一小两个正方形,说说你们的拼搭方法,并利用这种拼搭方法回答“勾三,股四,则弦几何”的问题.
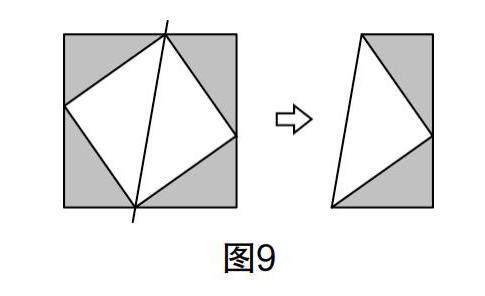
变式2按照图9的方式裁剪图形,能否回答“勾三,股四,则弦几何”的问题?
评注此例题的设计基于数学文化渗透,将枯燥的例题教学转化成风趣的操作思考问题,尤其是变式的应用,学生不但亲历动手、动脑的过程,还在直观操作的感性体验中获得理性思考,形成更多的活动经验,这对锻炼学生的发散性思维与灵活性思维具有重要的促进作用,同时还有助于培养学生的数形结合思想,为后续研究更多的几何问题奠定基础.
4. 归纳定理,提炼总结,巩固提升
课堂中,大量零碎信息会对学生的大脑形成较大冲击,此时学生的知识结构尚不稳定,尤其是新旧知识之间因存在一定的联系而容易混淆. 因此,课堂结束前的小结环节显得尤为必要,它能帮助学生厘清知识间的内在联系.
本节课,总结引导设计如下:
问题1华罗庚曾经说过:“若世界上真的存在外星人,那么勾股定理就是人类与他们取得联系的主要方式.”结合本节课我们对勾股定理的认识,说说你们对这句话的理解.
问题2大家在本节课有什么收获?还存在哪些疑问?有没有需要继续深入探索的问题?
学生在这两个问题的引导下对本节课的学习进行了总结,并谈了一些体会,教师有针对性地进行了补充. 为了让学生充分感知勾股定理在数学学习中的重要性,教师可再次从数学文化的角度进行课堂总结,以激发学生的探究兴趣.
总结 勾股定理是迄今为止世界上证明方法最多的定理之一,近几百年内就涌现出四百多种证明方法,而这些证明者并非清一色的数学家,为什么古往今来大家都乐此不疲地寻找勾股定理的证明方法呢?这也凸显了数学独有的魅力.
几何与代数是数学的两大脉络,而勾股定理既是一种几何性质,又是一个代数关系,因此它的证明路径较为广泛,课后如果大家有兴趣,可以查阅资料,下节课我们一起展示多样化的勾股定理证明方法.
评注本节课以《周髀算经》中的一则小故事切入教学主题,成功地激发了学生的学习兴趣,为接下来的探究活动奠定了良好的情感基础. 教学过程中,教师将课堂还给学生,充分发挥学生的主人翁意识,通过自主探索与合作交流的方式有效地培养了学生的探究精神. 整个教学过程都体现出浓郁的数学文化气息,有效地激发了学生的爱国热情,发展了学生的数学核心素养.
总之,在“新课标”的引领下,想要从真正意义上提升学生的数学核心素养,数学文化的渗透必不可少. 这就需要我们教师在教学实践中加强探索、深入思考,通过各种途径不断丰富自身的知识储备,提升专业技能与素养,让文化之花绽放在每个学生的心田.

