圆锥曲线上定点定值子弦性质的另证与应用

江浩

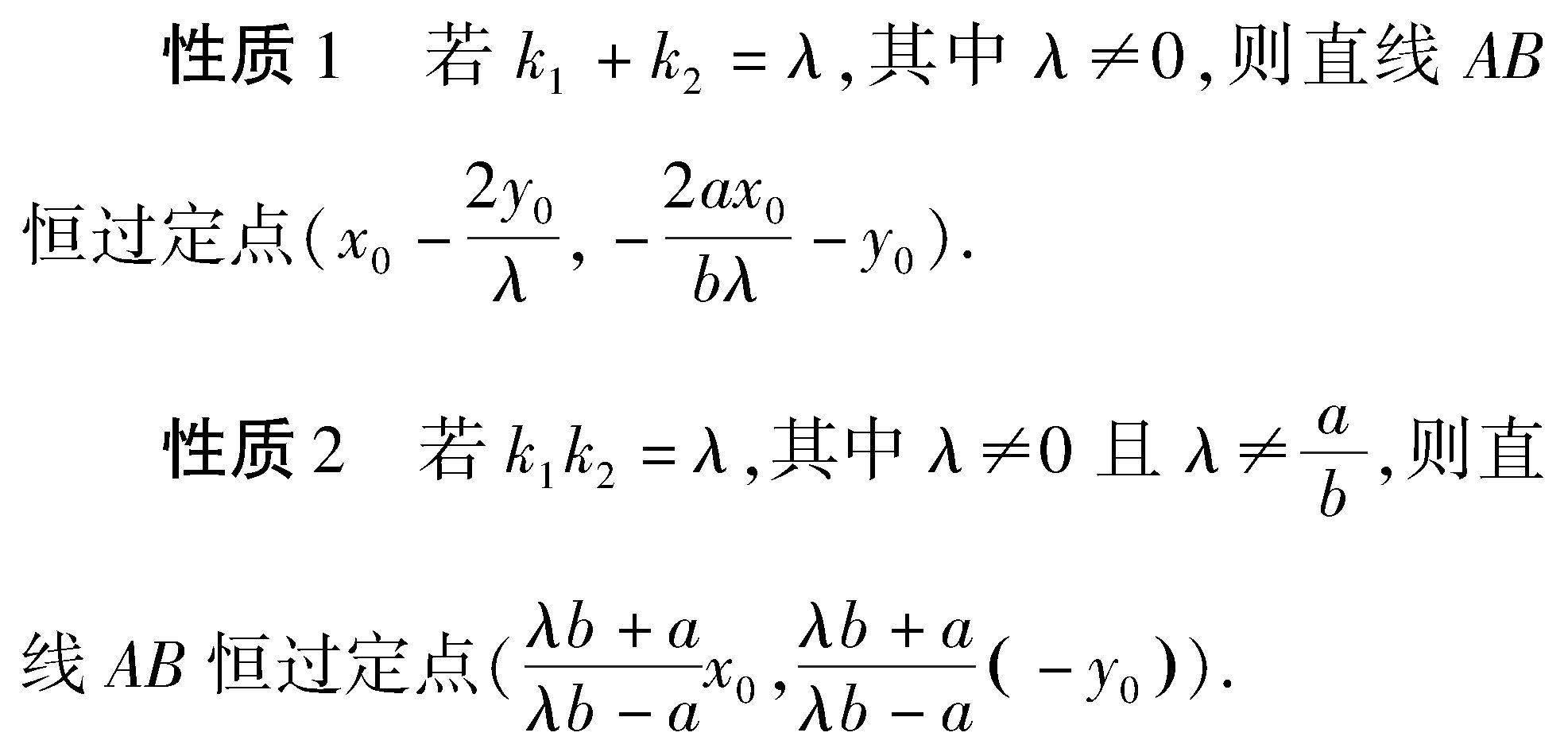
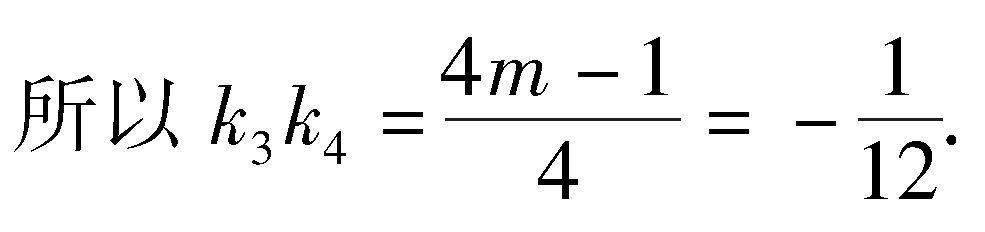
摘 要：研究了圆锥曲线上定点关于定值λ的斜率等和与等积子弦的性质，通过利用平移齐次化方法证明了更一般化的结论.结合具体实例，体现了所给的性质以及证法能够解决解析几何中一类斜率之和或积为定值的问题，旨在帮助学生能够迅速找到解决此类问题的突破口.

关键词：圆锥曲线；定点；定值；子弦；应用

中图分类号：G632   文献标识码：A   文章编号：1008-0333（2024）07-0085-03

2013年刊发的文[1]给出了圆锥曲線上定点定值子弦的定义[1]，利用联立方程组的方法证明了斜率等和与等积子弦的相关性质.文章研究内容是近几年高考考查的热点问题，比如2020年新高考Ⅰ卷第22题，2022年新高考Ⅰ卷第21题，2022年全国高考理科乙卷第20题均涉及此类问题，这是广大考生感觉到非常困难的问题.文[2]提出平移齐次化方法是处理这类问题的一种非常有效的手段[2].本文将基于一般化的圆锥曲线形式，利用平移齐次化方法证明定点定值子弦的相关性质，结论形式更加统一，证明过程更加简洁.

1 圆锥曲线上定点定值子弦的定义

设点P是圆锥曲线上的一个定点，PA，PB是该曲线过定点P的两条弦，当直线PA，PB的斜率之积为定值λ时，称线段AB为该曲线上定点P的关于定值λ的斜率等积子弦；当直线PA，PB的斜率之和为定值λ时，称线段AB为该曲线上定点P的关于定值λ的斜率等和子弦.

2 定点定值子弦的性质及其证明

2.1 椭圆与双曲线上定点定值子弦的性质

过曲线（椭圆或双曲线）Γ：ax2+by2=1ab≠0上一个定点Px0，y0分别作两条不同直线l1，l2与曲线Γ相交，另外两个交点分别为A，B，设直线l1，l2的斜率均存在且均不为0，将其分别记为k1，k2.

证明 将平面直角坐标系xOy进行平移，使得坐标原点与点Px0，y0重合，则曲线Γ的方程变成ax+x02+by+y02=1.展开可得

ax2+2ax0x+ax20+by2+2by0y+by20=1.

又ax20+by20=1，则ax2+2ax0x+by2+2by0y=1.

设直线AB：mx+ny=1，所以

ax2+2ax0xmx+ny+by2+2by0ymx+ny=1.

结合图形可知，k1，k2就是该方程的两个不相等的实数根，于是有

则2by0m=-2ax0n-2by0nλ-bλ.

直线AB方程两边同时乘以2by0，将上式代入，整理可得

-2ax0x-2by0λx+2by0yn-2by0-bλx=0.

则2ax0m=λb-a+2bλy0n.

同理可将AB方程整理成

2bλy0x+2ax0yn+xλb-a-2ax0=0.

注1 从证明过程可以看出，当曲线Γ表示圆时，上述结论已成立.

2.2 抛物线上定点定值子弦的性质

过抛物线Γ：y2=2pxp>0上一个定点P（x0，y0）分别作两条不同直线l1，l2与曲线Γ相交，另外两个交点分别为A，B，设直线l1，l2的斜率均存在且均不为0，将其分别记为k1，k2.

上述性质的证明与性质1、2的证明方法类似，这里不再赘述.

3 应用举例

又AD⊥MN，所以点D在以AB为直径的圆上，

记直线AB，AC斜率分别为k3，k4，

设AM：y=k3x+2，可得M0，2k3.

注3 当不能确定某条线段是否是曲线上定点的关于某个定值λ的斜率等和或等积子弦时，可以利用证明性质1，2的方法去探究.

4 结束语

圆锥曲线中的定点与定值问题是历年高考必考内容之一，也是广大师生处理起来比较棘手的问题.本文研究了圆锥曲线上定点定值的斜率等和与等积的子弦问题，揭示了过圆锥曲线上一个定点的两条直线斜率之和或者之积为定值时，两交点构成的第三条直线恒过定点的重要特征，也可以逆向使用这些性质特征，即已知直线恒过定点，可以推断另外两条直线斜率之和或之积为定值，这可以为研究圆锥曲线问题提供一个重要线索，为解决问题找到突破口.“授人以鱼，不如授人以渔”，平移齐次化方法更加值得我们关注，它是处理此类问题的一个非常奏效的方法.

参考文献：

［1］曹军.圆锥曲线上的定点定值子弦的性质：圆锥曲线顶点定值子弦性质的推广[J].中学数学研究，2013（19）：19-21.

[2] 李斯乔，蔡明，李宁.齐次化联立解决涉及斜率和或积的定点定值问题[J].数学通讯：2020（17）：60-62.