大地坐标换算施工坐标在地铁车站施工中的研究与应用

杨晓冬

(上海市基础工程集团有限公司,上海 200002)

0 引言

地铁建设作为现代城市交通发展的重要组成部分,对于城市快速、高效、便捷的交通需求起着至关重要的作用。在地铁车站的施工过程中,准确的坐标定位是确保施工质量和进度的关键因素之一。由于车站设计是在城市总体规划基于大地坐标系下进行的,因此导致建筑物的轴线方向与大地坐标系统不是平行关系,计算也比较复杂,且不够直观。而施工坐标系则不同, 施工坐标系是根据测量工作需要建立的一种坐标系,使用起来比较方便。本次研究工程车站距离较长,施工面积较大,如果采用大地坐标系进行控制,不易于计算,且加大了放线的难度。为实现计算的便捷性,应将施工坐标系与大地坐标系的坐标进行换算使其统一,从而实现地铁车站施工过程中的轴线控制的便捷性,进而提高测量放线的效率。

1 大地坐标与施工坐标的概述

大地坐标转施工坐标是一个将全球或区域性的坐标系统(如WGS-84或CGCS2000)转换成适用于具体建设项目的本地坐标系统的过程[1]。这个过程在工程建设、构筑物定位中非常重要,因为它确保了设计图纸和现实世界之间的准确对应关系。

大地坐标系统:基于地球模型的坐标系统,使用经度、纬度和高程来定位地球表面的点。常见的大地坐标系统包括WGS-84(GPS使用的坐标系统)和CGCS2000,或者其他的地域性的坐标系统[2]。

施工坐标系统:施工坐标是指在施工现场建立的一种局部的坐标系统,用于描述施工过程中各个构筑物或测量点的位置。通常选择施工现场的某一固定点作为原点,根据施工任务的要求,确定合适的坐标轴方向。如选择北方向为X轴正方向,东方向为Y轴正方向。根据施工现场的实际情况,确定合适的坐标单位。转换过程通常包括平移(改变原点位置)、旋转(改变方向)和缩放(改变尺度)等步骤。这个过程虽然技术性较强,但对于确保工程项目的精确实施至关重要。正确地进行坐标转换能够显著提高施工效率和质量。

2 大地坐标转换施工坐标计算原理

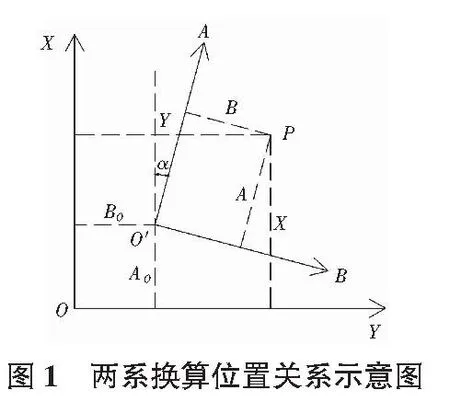
由图1 可知,XOY为大地坐标系的坐标轴,AO′B为施工坐标系的坐标轴,已知P点在大地坐标系统中的坐标为(XP,YP),在施工坐标系中的坐标为(AP,BP),施工坐标系原点O′,在大地坐标系中的坐标为O,角α为大地坐标系的纵轴X与施工坐标系纵轴A的夹角,即两坐标系的旋转角。依据图形间的几何关系即可推算出它们之间的换算关系,点P由大地坐标系转换为施工坐标系公式为[3]:

AP=(XP-AO)cosα+(YP-BO)sinα。

BP=-(XP-AO)sinα+(YP-BO)cosα。

施工坐标系转换为大地坐标系公式为:

XP=AO+Acosα-Bsinα。

YP=BO+Asinα+Bcosα。

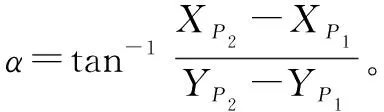
3 坐标转换应用实例

3.1 工程概况

城北路站为上海轨道交通市域线嘉闵线工程第一座车站, 本站为地下2层12 m岛式车站。车站外包总长632.2 m,标准段宽21.8 m,为单柱双跨、局部双柱三跨箱型框架结构。整个车站由西向东纵向找坡0.2%,车站顶板埋深约2.8 m～4.2 m,中心里程处车站基坑深度约20.4 m,西端头井基坑深度约22.4 m,东端头井基坑深度约23.8 m,采用明挖顺作法施工。

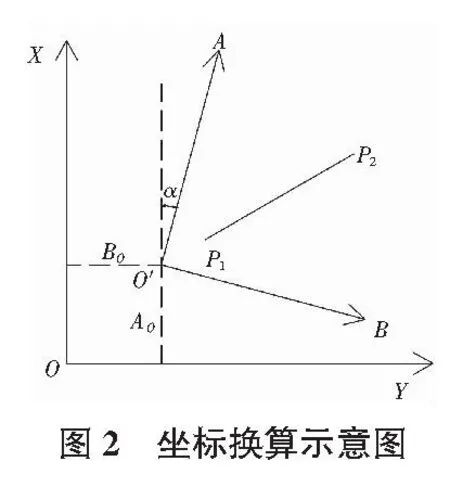
3.2 施工坐标系在地铁车站施工中的建立与应用

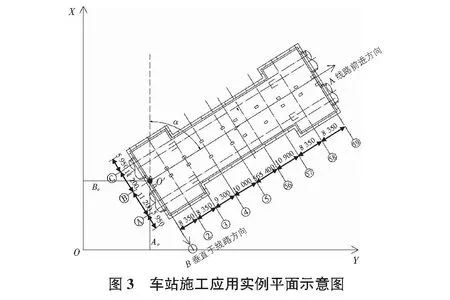
本工程设计交桩平面控制点采用上海城市坐标系统(可视为大地坐标系),车站施工过程中将大地坐标系统转换为施工坐标系统进行施工放样。如图3以车站轴网前进方向B轴设为X(A)方向,轴网纵轴设为Y(B),以车站中线1/B轴为坐标原点进行转换,依据轴网设计图纸提供的坐标计算得出,交点1/BX=(+17 657.362,Y=-22 706.466),交点59/BY=(+17 987.437,-22 171.030),通过两点坐标对车站建筑进行两系坐标换算的已知参数。

现以其中一点的坐标换算为例:已知控制点P,其在大地坐标系统中的坐标为(X=+17 987.437,Y=-22 171.030),通过上述公式换算施工坐标系:

AP=(XP-AO)cosα+(YP-BO)sinα。

BP=-(XP-AO)sinα+(YP-BO)cosα。

即:

AP=(17 987.437-17 657.362)cosα58°20′52.15″+(-22 171.030+22 706.466)sinα58°20′52.15″=629.000。

BP=-(17 987.437-17 657.362)sinα58°20′52.15″+(-22 171.030+22 706.466)cosα58°20′52.15″=0。

由此得到了待求点的施工坐标。依据上述计算实例并对测绘院提供的控制网坐标进行换算可得成果表见表1,通过换算的控制网坐标进行后续的施工放样。

3.3 大地坐标系与施工坐标系计算方法对比

由此,已经解得本工程中大地坐标系和施工坐标系两套控制网系统的数据。在此基础上,对比两种测量设计值的计算过程。

4/AX=17 657.362+28.310×cos58°20′52.15 ″+23°18′16.71″=17 661.472 0。

4/AY=-22 706.466+28.310×sin58°20′52.15 ″+23°18′16.71″=-22 678.455 9。

通过计算可以发现,采用大地坐标系测量方法,计算过程烦琐,且得到的坐标值位数长,加大了数据输入全站仪时输错的概率,且不利于后续偏差的计算。此方法如果用于少量点位计算时,产生的诸多不利因素尚可人为把控。但在实际的车站施工中,需要对梁、板、柱等进行定位放样,计算点位多则成百上千个,显然这个方法在大量点位计算中不占优势,且容易出错。虽然可以在内业中提前利用CAD或者Excel进行计算[5-6],但在实际的施工中提前计算好的点位大概率会受场地、堆物、机械施工等因素影响,并不能按照提前计算好的数据进行放样,须依据现场的实际情况进行点位计算。在此前提下,则需要运用一个更理想的计算方法。而利用施工坐标进行某点位放样,就可以完全避免计算问题。

通过研究建立的施工坐标系的方法,所得到的施工坐标,输入到全站仪进行设站,全站仪在设站时是通过转换后的施工坐标进行的,以此作为放样的基准线,且基准线是处于施工坐标系统下的。同样计算4/A轴的交点坐标,通过设计图纸标注的纵向距离36 m,横向距离11.2 m,再观察点位所在象限(见图3),即可得出此点的施工坐标(A=36,B=11.2),无需再进行复杂的计算,通过设计图纸标注的横纵尺寸得出设计坐标值,在此过程中只需判定点位象限即可[7]。而车站施工中梁柱一般采用对称设计,在建立施工坐标系时同样采用车站中心线建立。这种建立方法,其优势在于只需要得出一侧的标注尺寸,对称一侧的设计值取B轴的相对值即可,即对称点设计值为A=36,B=-11.2,由此计算得出中线两侧的所求点位设计值。

这种方法在直线长距离放样中也有比较显著的优势,本工程设计车站总长约632.2 m,属于超长距离车站。车站设计中,板、墙设计一般为直线走向,通过此方法,在这632.2 m侧墙施工轴线控制中极大地提升了放线速度,并且可以消除纵轴带来的测量误差。控制轴线只需要在控制线起点与终点考虑横纵(A,B)值,在侧墙0 m～632.2 m间只需要控制侧墙的偏距(B)值即可。通过设计图纸可得,侧墙至纵轴横向偏距为11.2 m,侧墙放样过程中11.2 m就是B轴控制轴方向的固定偏距值。过程中A值代表定位点与起终点之间的距离,控制平行轴线时可忽略。如此不但可消除在放样过程中A值所带来的测量误差,而且设计值也无需进行烦琐的计算,便可实现直线上任意点位放样,完美解决了长距离侧墙施工中障碍物对放线的影响,极大提高了放线速度和精度,确保了施工质量。

3.4 施工坐标系在盾构钢环定位中的研究与应用

地铁隧道施工前,需要在车站结构中预埋洞门钢环,洞门钢环安装施工也是地铁车站主体结构施工中一个至关重要的工序。钢环的安装精度,则是后续盾构机顺利出洞的重要保障[8]。常规的安装方法一般是在地下连续墙面上,放样出钢环圆心坐标,设计中钢环一侧与车站侧墙处于同一平面上,还需要在洞环下方放样出侧墙轴线,此轴线结合线垂法控制钢环的旋转与倾斜,再利用钢卷尺量取钢环与地下连续墙圆心点的相对关系,进行钢环的上下左右控制。这个方法在大直径钢环量取中,不能保证量尺直线下垂,直接造成测量误差,因此还需利用全站仪通过圆心拟合的方式进行复核测量计算,圆心拟合计算极其复杂,一般是在钢环固定完成后,测量钢环3个及以上的三维坐标值,推算出钢环的空间圆心位置,得出钢环偏差[9]。此方法由于计算复杂,测量烦琐的特性,移位过程中不能实时得到准确的偏差值,这就导致钢环固定后测量偏差过大,需二次返工,造成直接经济损失。

通过研究的施工坐标系测量方法同样适用于三维空间下,本工程施工钢环安装是通过两次安装定位,即上半环和下半环。下半环安装固定完成后进行混凝土浇筑,待混凝土强度达标后,可进行钢环的上半环安装,通过设计图纸得出钢环直径,并计算得出钢环的圆心坐标及高程(见表2),进行施工坐标转换。同时标高也可以进行转换,钢环实测标高是通过全站仪三角高程测量所得[10]。洞门设计中心标高与架仪点都存在一个绝对标高值,再利用测站绝对标高值减去洞门设计标高值,依据两点绝对标高发生变化相对高度是一致的这一原则,同样可以把洞门设计中心标高Z=-10.906 m转换为0,方便后续偏差计算。

表2 盾构钢环控制点转换成果表

依据转换成果表,利用控制点坐标及高程XL1与XL2进行设站,见图4,测量过程中全站仪是可以进行三维坐标测量的,即(X,Y,Z)[11-12]。在上半环和下半环各测3个及以上固定点位。首先计算出钢环固定点位的设计值,钢环定位点是设在施工坐标系对应的横轴与纵轴的垂直方向,已知钢环φ=9.6 m,R=4.8 m,设定钢环圆心坐标(A=0,B=0,H=0),只需观察象限即可得出测点1(A=0,B=-4.8,H=0)、测点2(A=0,B=+4.8,H=0)、测点3(A=0,B=0,H=-4.8)的设计值。测量过程中,通过设计值和实测值的对比就可得到钢环偏差。X(A)轴可以控制钢环的前后位置,Y(B)轴可以控制钢环的左右位置,Z(H)轴可以控制钢环的上下位置。同理如图5所示,在安装过程中钢环会出现前倾或者后倾的情况,在此基础上只需要控制X(A)轴上下皆为0即可,钢环左右倾斜亦是同理。在测量过程中偏差值无需进行烦琐的计算,并且过程中是利用全站仪免棱镜模式进行实时测量的,实测值与设计值只需简单的加减运算即可得出偏差值。对吊装过程中的钢环就可进行实时调整,避免了钢环固定后的二次调整,钢环调整完成后,再次对固定完成后的钢环进行测量,如图4所示。

通过对安装完成后的钢环进行偏差检测(见表3),可以看出通过此方法可以将偏差控制在±5 mm以内,大大提高了钢环的安装精度,提高施工质量。

表3 钢环安装完成后测量偏差

4 结论

通过以上案例分析,可以看出大地坐标换算施工坐标在地铁车站施工中的重要应用价值。随着现代建筑设计复杂、施工要求及科技的提高,测量精度要求相应也跟着提高。这无形给施工测量放线工作带来了极大的难度和工作量。如文章案例所示城北路站为地下2层12 m岛式车站,车站外包总长632.2 m,段宽21.8 m,又分为单柱双跨、局部双柱三跨箱型框架结构。工程面积大,分部多,对于测量放线要求比较高。而将所研究的施工坐标系统的测量运用到本车站中,则取得了良好的应用效果。

通过实践,施工测量过程中,当工程结构复杂,测量范围较大时,为了保证测量准确度和施工效率,使用施工坐标系的测量办法是比较简便且准确的测量方式。很大程度上提高了工程经济效益和施工质量。笔者认为此方法也适用于其他建筑类工程中,如房建、桥梁、隧道等工程中。因此大地坐标转施工坐标系统的测量方法具有很好的应用前景,此方法值得在各个工程领域广泛推广,并在今后的工程实践中不断提高和完善。