地铁盾构隧道洞门钢环精密检测与数据处理方法研究
邓 哲
(江苏经贸职业技术学院, 江苏 南京 341000)
0 引言
在使用盾构进行地铁隧道施工时,需要在车站始发与接收井开挖洞门并预埋钢环,在成型的钢环外侧采用加厚的混凝土井壁支撑整个洞门,而钢环内侧则采用薄水泥井壁,以便隧道贯通时盾构破壁而出[1]。在始发与接收车站安装洞门钢环主要有3方面作用:1)将车站结构与混凝土管片连接为整体,有利于车站主体结构与隧道区间节点处的防水,避免盾构在出洞(或进洞)因始发(或到达)井端头涌水而造成地面坍塌以及盾构掩埋[2];2)作为始发井的重要标志,为盾构准确安装和始发提供重要保证[3];3)为盾构始发与到达提供平面、高程和方位等参数依据[4]。
洞门钢环与隧道管片不同,隧道管片由于长期承压导致变形后呈现椭圆特征,而洞门钢环较稳定,呈现为一个标准圆环。但洞门钢环的制作、放样和安装均存在误差,使得钢环的实际位置与设计位置不一定重合,严重时会出现错位现象,致使产生涌水、涌砂、土体坍塌等施工事故[5]。为了确保盾构按设计线路顺利进出洞,需要对已安装洞门钢环的圆心、半径、平整度、垂直度、圆度等参数进行空间形态检测与分析。上述洞门参数均无法直接测量,工程实践中通常采用智能全站仪测量洞门钢环上一系列点的三维坐标,然后通过拟合的处理方法间接得到洞门参数,再与设计值进行比对,完成洞门钢环的检测与质量评价。
国内许多学者已对洞门钢环的检测与数据处理方法进行了研究,大部分均可归结为先拟合空间球体再拟合空间平面的两步解法,但该方法在得到拟合参数后需进一步计算洞门参数,计算过程略显复杂且不具备抗差性,观测点沿洞门平面法线方向的误差会对拟合结果产生很大的扰动[6-8];文献[9]借助AutoCAD软件通过多组3个观测点绘制空间球体功能构建并捕捉多组球心坐标,再将所有球心坐标通过AutoCAD软件构建成一个面域,并利用属性查询功能得到洞门钢环的中心坐标,但该方法对洞门钢环的空间分析并不实用,无法得到平整度、垂直度、圆度等洞门参数,一旦工程实践中上述参数不达标,会导致盾构进出洞时碰撞洞门四周,造成施工事故。本文针对上述问题,根据空间几何理论提出一种直接获取洞门圆心、半径、平整度、垂直度、圆度等参数的方法,并结合随机抽样一致性算法(RANdom Sample Consensus,RANSAC)[10]逐步剔除测量数据中含有较大误差的观测点,减小测量误差对拟合结果的扰动,最后在Microsoft Visual Studio 2016平台运用C#编程语言将所提算法程序化,对南京轨道交通5号线五台山站洞门钢环实测数据进行处理,得到了较好的应用效果,研究成果以期为地铁洞门钢环精密检测与分析技术提供新的参考。
1 地铁洞门钢环精密检测方法
1.1 检测要求
在地铁洞门钢环检测时通常要求: 1)钢环中心三维坐标点位偏差不超过10 mm; 2)钢环内径允许差不超过10 mm;3)钢环所在空间平面的平整度不超过6 mm; 4)钢环所在空间圆的圆度不超过6 mm; 5)钢环所在空间平面与设计平面角度偏差不超过0.016°; 6)任意点内径误差不超过10 mm。根据上述对洞门钢环检测的限差要求,可以将洞门钢环安装后的空间形态归为洞门钢环的中心坐标、半径、平整度、圆度和垂直度等几个主要方面。
1.2 检测设备及方法
地铁洞门钢环三维坐标测量精度直接影响洞门的拟合效果,目前洞门钢环检测仪器仍以全站仪为主,有条件的情况下可以采用激光跟踪仪[11]跟踪测量采集检测数据。地铁洞门钢环精密检测前,需在地下施工水平面洞门附近建立控制点标志,控制点标志尽可能采用强制对中装置,以减小仪器对中误差、高量测误差等对检测结果的影响;其次,采用合理的联系测量方法[12]将地上平面坐标系统和高程系统传递到地下控制点,并通过导线测量和水准测量将平面和高程基准传递到位于洞门附近的强制对中装置;最后,在强制对中装置上安装全站仪或激光跟踪仪,采用三维坐标法[13]测量洞门钢环上一系列特征点的三维坐标。
为避免洞门钢环空间形态拟合时出现病态方程,全面真实地反映整个洞门钢环的空间形态,需在洞门钢环内环按照图1所示的分布情况均匀粘贴具有足够密度的若干反射片,且洞门的上、下、左、右端必须安置反射片,在平面坐标和高程已知的地下控制点上安置高精度全站仪,采用反射片测距模式测量反射片的三维坐标。此外,实际测量时应尽量增加检测点的数量,测量的反射片至少为4个,检测点数量越多,对于全面真实地分析钢环各点的空间形态更为有利。

图1 洞门钢环测点布设示意图
2 基于RANSAC的地铁洞门钢环空间形态计算

2.1 洞门钢环空间形态拟合参数的一步解法
设洞门钢环所在的空间平面方程为:
ax+by+cz+d=0。
(1)
式(1)中a、b、c、d是线性相关的,由线性代数理论可知式(1)含有无数组解[14]。为了得到系数的固定解,在式(1)等号两边同时乘以一个非零的比例系数,将d化为1:
ax+by+cz+1=0。
(2)

(x2-x1,y2-y1,z2-z1)·
(3)
对式(3)化简得中垂面方程为:
(4)
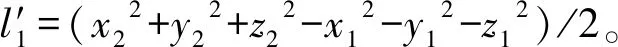
由于洞门钢环圆心P0(x0,y0,z0)位于洞门钢环所在的空间平面,所以当观测点数目为n时,可列出2n个线性无关的方程式,包括1个圆心平面方程式、n个空间平面方程式和n-1个中垂面方程式,则洞门参数的误差方程式为:

(5)
式中:

(6)
(7)
根据最小二乘准则VTPV=min,通过式(8)可计算洞门钢环圆心坐标与空间平面系数的改正值,将其与初值融合便可得到最或是值。
(8)
式(8)中计算的洞门圆心坐标位于重心化后的坐标系,应将其平移到测量坐标系,以便与设计坐标进行比对。根据计算的洞门圆心P0重心化后的坐标(x0,y0,z0),结合各观测点重心化后的三维坐标Pi(xi,yi,zi),通过式(9)可计算洞门钢环的半径。当观测点数目为n时,应计算所有观测点对应的半径并取其平均值作为洞门钢环半径的最或是值。
(9)
2.2 基于RANSAC算法的洞门钢环空间形态迭代计算
洞门钢环检测数据采集过程多采用全站仪测量粘贴在钢环内环的反射片,由于测量时的光轴入射角等原因可能致使测量错误或产生较大的测量误差。RANSAC算法可以找出并剔除误差较大的观测点,以及减少观测点沿洞门平面法线方向的误差对拟合结果产生的扰动影响,最终达到提高拟合模型精度的目的。基于RANSAC算法的洞门钢环空间形态迭代计算的具体步骤如下。
1)借助2.1节所述方法,根据所有测量的观测点Pi重心化后的三维坐标(xi,yi,zi)拟合洞门钢环的空间形态。
2)联合洞门钢环所在空间平面的系数(a,b,c)与观测点的坐标(xi,yi,zi),分别通过式(10)、式(11)计算所有观测点Pi到洞门钢环所在空间平面的距离Δdi和到圆心的距离与半径的差值Δri:
(10)
(11)
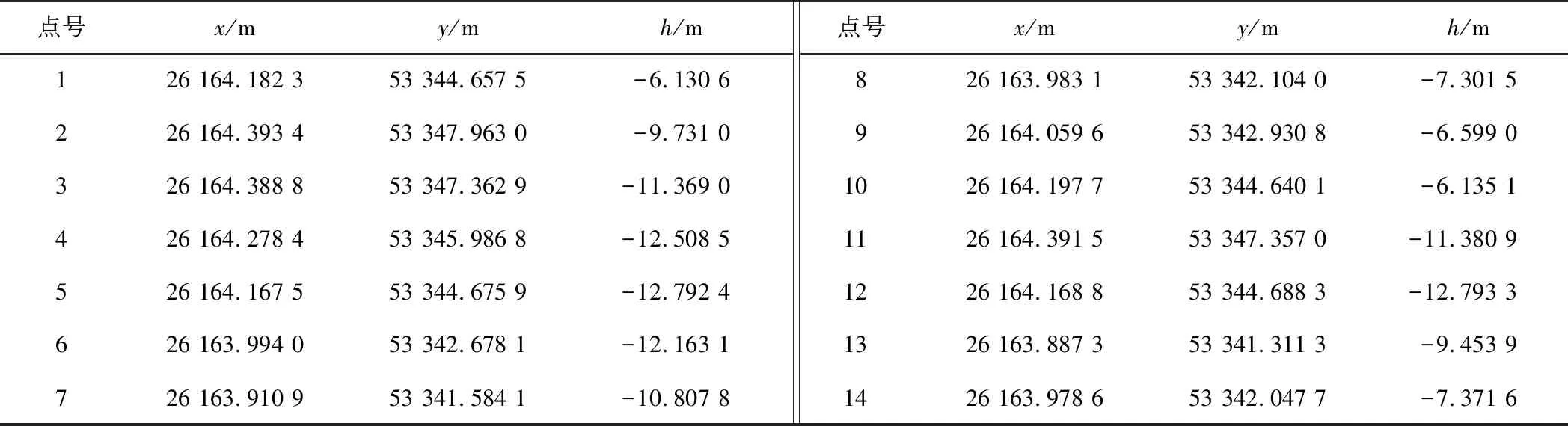
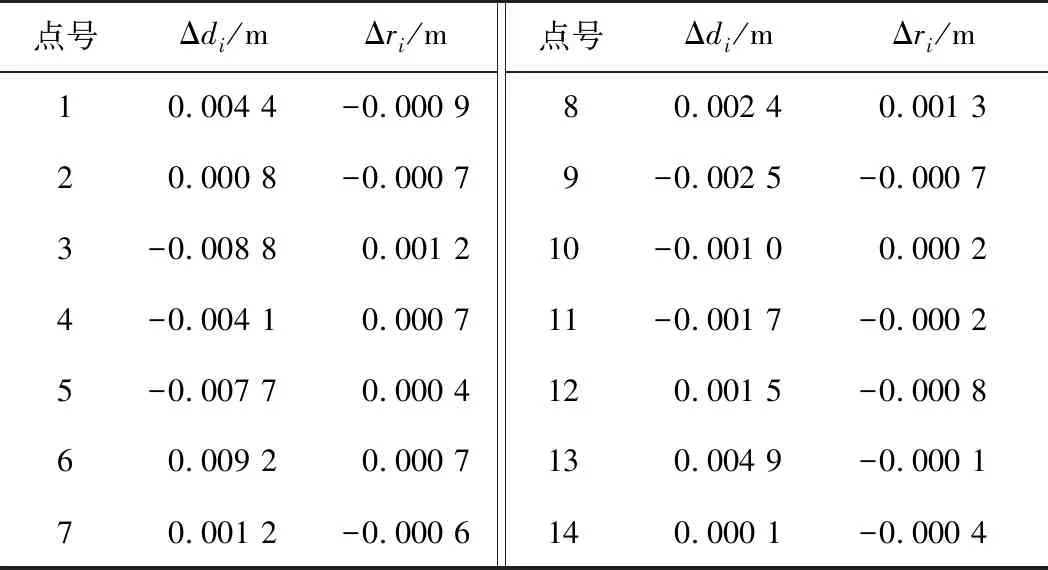
3)根据工程实际情况确定阈值K1和K2,当|Δdi| 4)当局内点数量大于观测点集的90%时,可以精确拟合洞门钢环的空间形态;当局内点数量小于观测点集的90%时,应删除所有局外点,对剩余局内点重复步骤1—3,直至局内点数量大于观测点集的90%时为方可停止拟合迭代。 5)利用最终得到的观测点集Wi,重新计算洞门钢环的圆心坐标、半径、平整度、垂直度和圆度等洞门参数。 地铁盾构隧道洞门钢环检测及数据处理的整个工作流程如图2所示。 图2 地铁洞门钢环检测及数据处理流程图 Fig.2 Flowchart of metro portal steel ring detection and data processing 在拟合洞门参数后,需要根据洞门参数对隧道洞门钢环的空间形态进行分析,主要包括以下2个方面。 1)分析洞门钢环安装位置与设计位置存在的差异。安装后的洞门钢环圆心可通过上文所述的拟合方法计算得到,而安装后的洞门钢环所在空间平面的法向量(a,b,c)与洞门钢环设计时的空间平面法向量(a′,b′,c′)之间的夹角可定义为洞门的垂直度。洞门圆心和垂直度是评价洞门钢环安装位置与设计位置差异的重要指标。 2)分析洞门钢环安装形状与设计形状存在的差异。洞门钢环的平整度、圆度和圆半径是评价洞门钢环安装形状与设计形状差异的重要指标,通过式(10)可计算各观测点到洞门钢环所在空间平面的距离,以及通过式(11)可计算各观测点到洞门圆心距离与半径的差值,这些距离是安装过程中造成的一种偶然误差,致使洞门安装形状与设计形状存在差异,因此可通过式(12)、式(13)计算这些距离的均方根差,用于表达洞门钢环的平整度和圆度。 (12) (13) 在Microsoft Visual Studio 2016平台用C#编程语言将本文算法程序化,实现了洞门钢环的拟合计算、平整度计算、圆度计算、垂直度计算、数据入库功能。以南京轨道交通5号线五台山站洞门钢环作为研究对象,在洞门内环等间隔粘贴15个Leica反射片作为观测点,在隧道洞门的正前方采用自由设站法安置标称精度为(0.5″,1 mm+1×10-6D)的Leica TM30测量机器人,测量15个反射片的三维坐标。 为验证RANSAC算法在洞门钢环空间形态精确拟合中的可行性以及抵抗法线方向误差对拟合结果的扰动效果,在第15号观测点的X、Y坐标上加入0.5 cm粗差,带入自制程序后发现能够将第15号观测点甄别为局外点,采用剔除第15号点的其余洞门原始观测数据(见表1)精确拟合洞门钢环的空间形态。 将表1中的观测数据录入到自编程序,拟合计算模型参数最优估计量,得到该洞门钢环的半径为3.343 m、洞门的圆心坐标为(26 163.941 5, 53 344.654 3, -9.465 1);将洞门钢环的圆心和所在空间平面的法线向量与洞门钢环的中心设计坐标和法线向量进行比对,计算得到洞门圆心的点位偏差为1.7 mm、垂直度为0.003°。此外,计算各观测点到洞门钢环所在空间平面的垂直距离和到圆心的距离与半径的差值,结果见表2。 表1 剔除异常观测值的洞门钢环各点坐标原始观测数据 表2洞门钢环各点到洞门空间平面的垂直距离和到洞门圆心距离与半径的差值 Table 2 Distance from point of portal steel ring to portal space and distance between center and radius 点号Δdi /mΔri /m10.004 4-0.000 920.000 8-0.000 73-0.008 80.001 24-0.004 10.000 75-0.007 70.000 460.009 20.000 770.001 2-0.000 6点号Δdi/mΔri/m80.002 40.001 39-0.002 5-0.000 710-0.001 00.000 211-0.001 7-0.000 2120.001 5-0.000 8130.004 9-0.000 1140.000 1-0.000 4 由表2可知,各观测点到洞门钢环所在空间平面的垂直距离最大为0.009 2 m,最小为0.000 1 m,通过式(12)计算得到洞门钢环平整度为0.004 6 m;观测点到洞门圆心距离与洞门半径的差值最大为0.001 3 m,最小为-0.000 1 m,通过式(13)计算得到洞门钢环圆度为0.000 7 m。 综合分析洞门圆心、半径、平整度、垂直度和圆度等评价洞门钢环空间形态的参数,发现南京轨道交通5号线五台山站洞门钢环空间形态良好,没有发生较大变形情况。此外,通过本文开发系统的“数据入库”功能,将本期外业检测原始数据和质量分析结果保存到系统的数据库中,后期进行跟踪测量,为对比分析各期检测数据结果以及评价洞门变形提供数据支撑。 1)根据洞门检测点的空间几何关系推导了用于构建误差方程的中垂面方程,提出了洞门钢环空间形态拟合参数的一步解法,并采取随机抽样一致性算法克服了检测点误差对拟合结果产生的扰动。 2)将所提算法程序化,利用自编程序和实测数据对南京轨道交通5号线五台山站洞门钢环进行空间形态分析,取得了良好的应用效果。 3)研究的洞门钢环精密检测与数据处理方法也为地铁工程的盾构隧道管片检测以及盾构制造和组装过程中的盾尾尺寸检测工作提供了参考。 随着施工技术的不断发展,圆形盾构的洞门钢环检测技术已无法满足现今异形盾构的需要,建议下一步对适用于马蹄形、双圆形、三圆形、类矩形等异形洞门的精密检测与数据处理方法提出一整套解决方案。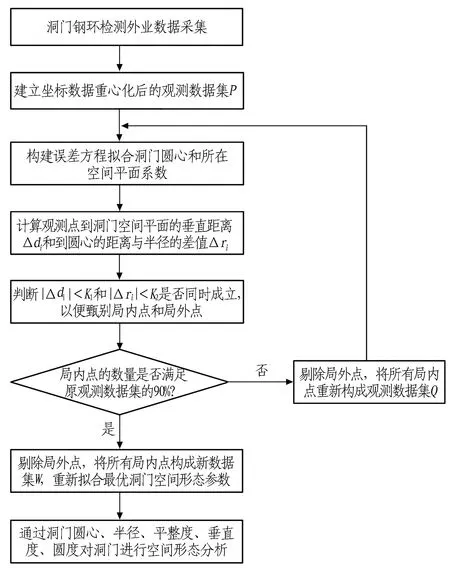
3 洞门钢环空间形态分析
4 实例计算与分析
5 结论与建议

