温度荷载下剑麻纤维-ECC地下侧墙抗裂性能

崔双双，陈润，陈艳，陈伟宏，王志东

(1.福建工程学院 土木工程学院，福建 福州 350118；2.福州大学 土木工程学院，福建 福州 350116)

随着大规模的地下工程建设，地下结构的侧墙(简称地下侧墙)开裂现象不断增多[1-2]。由于地下侧墙的开裂不仅会严重影响地下结构的耐久性，且修复难度大、费用高，因此对地下侧墙进行抗裂研究尤为重要。

为控制地下侧墙裂缝的产生，国内外学者利用粉煤灰等矿物掺合料来降低水泥掺量，以此控制结构水化热，提高混凝土的抗裂能力[3-4]。但由于不同工程条件各异，不能保证材料在不同工程中能够发挥可靠的抗裂作用。此外，在混凝土中加入膨胀剂会降低混凝土的收缩和由此产生的拉伸应力[5]，膨胀剂的用量难以控制，混凝土的开裂效果也不易保证。为此，需要寻找一种可靠、有效的建筑材料以解决地下侧墙的开裂问题。

工程水泥基复合材料(engineered cementitious composites，简称ECC)是基于微观力学系统设计的一种高延展性材料[6]，其拉伸应变可达到3%～7%，是普通混凝土的300倍[7-8]。ECC优异的控裂性能有利于其在地下结构抗裂工程中的应用，采用绿色环保价格低的剑麻纤维替换ECC中传统的增韧材料聚乙烯醇纤维，可降低成本[9-10]，且能够满足地下侧墙的工作性质及力学性能要求，具有良好的发展前景。

对于地下侧墙，温度及收缩变形是引起其开裂的主要因素，一般情况下，地下侧墙的温度变形主要由水泥水化温升引起，而收缩变形可通过转化为当量温差来考虑。为探讨将剑麻纤维-ECC应用于地下侧墙的抗裂效果，本文采用课题组前期研制出的性能优良的剑麻纤维-ECC材料配合比及其物理力学性能参数，借助ANSYS有限元软件，进行温度荷载作用下剑麻纤维-ECC地下侧墙及普通混凝土地下侧墙的热-结构耦合仿真分析。

1 地下侧墙模型建立

采用文献[11]中经过实际工程验证过准确性的普通地下侧墙ANSYS有限元建模方法，再现文献[11]中的普通混凝土地下侧墙模型，验证再现模型的准确性，然后将再现模型中的普通混凝土材料参数换成剑麻纤维-ECC材料参数，并根据混凝土温度场[12]及温度-收缩应力[13]的计算原理，对新型地下侧墙的温度收缩应力分析。本文考虑了温度变形(水泥水化放热引起)和收缩变形对剑麻纤维-ECC地下侧墙的开裂影响，这两个引起侧墙开裂的变形因素与文献[11]设计一致。普通地下侧墙模型再现及准确性验证可归纳为6个步骤：(1)选取算例与计算参数；(2)提出基本假定；(3)荷载选取；(4)确定边界条件及初始条件；(5)普通侧墙模型建立；(6)再现模型准确性验证。

1.1 普通地下侧墙模型建立

1.1.1 算例的工程概况及计算参数

某工程地下侧墙基本情况：总长36 m，墙厚0.4 m，墙高4.2 m。浇筑厚度为1 m的基础底板与高度0.4 m的墙体(吊模段)；14 d后开始浇筑3.8 m高的墙主体部分；墙主体部分浇筑3 d后，拆除20 mm厚的模板，拆模后发现地下侧墙出现竖向宽度为0.2～0.3 mm的贯穿裂缝(宽度超过0.1 mm的裂缝会渗漏水)。

在上述工程中，将强度等级为C40普通混凝土用于地下侧墙的有限元计算，建模中考虑了模板对温度场的影响(有限元中模板采用生死单元)，建模完成后将C40混凝土的相关参数替换成剑麻纤维-ECC的材料参数，之后分析侧墙的收缩应力。分析收缩应力时，需考虑的参数包括侧墙材料的配合比(见表1)，材料的热学性能(见表2)和力学性能(见图1及表3)。力学性能包括3个随龄期变化的因素：结构的弹性模量、泊松比与抗拉强度。其中不同龄期的材料弹性模量、抗拉强度分别由公式(1)(2)计算得到。

表3 侧墙材料的力学性能

图1 拉应力-应变全曲线

表1 侧墙材料配合比

表2 侧墙材料热学性能

E(i)=E0(1-exp(-0.09×i))

(1)

式中，i为龄期，d；E0为材料28 d后测得的弹性模量，kN·mm-1。

(2)

式中，Rf(i)为不同龄期的材料抗拉强度,MPa；i为龄期，d；Rf0为28 d后测试的材料抗拉强度，MPa。

1.1.2 基本假定与荷载选取

影响地下侧墙开裂的因素很多，故在有限元分析计算中使用如下假定：在弹性变形的范围内，侧墙材料是各向同性的均质材料；在静力及温度作用条件下，侧墙材料处于弹性变形范围内；地下侧墙均匀地收缩变形，基础底板的收缩变形在前期基本完成；侧墙材料的特性不随温度发生改变；不考虑框架柱及钢筋对地下侧墙的影响。

地下侧墙在施工期间主要受到温度荷载、结构自重以及结构收缩变形产生的荷载作用。其中，由于地下侧墙不高，因此可忽略墙体自重引起的横向膨胀变形，而收缩变形产生的荷载可转化为温度荷载。

1.1.3 确定边界条件及初始条件

在分析地下侧墙温度场时，基础底板的底部和侧面、侧墙的对称截面均采用绝热状态；基础底板上部、侧墙顶部同空气接触；另外，按照拆模前后与空气接触边界的不同，分为木模板表面与空气热对流边界条件和侧墙材料光滑表面与空气热对流边界条件。在分析地下侧墙应力时，由于与侧墙主体部分和基础底板相比，顶板的厚度较薄，因此可以认为墙主体部分与顶板的变形是同步的，由于本工程地下侧墙拆除模板时还未浇筑顶板结构，故认为墙体上端自由无约束；此外，基础底板的底部为固定约束，侧墙的对称截面以及基础底板的侧面给予垂直于该表面的位移约束。

由于本文以地下侧墙为研究对象，可假定施工期间的气温恒定，环境温度保持在22.92 ℃。基础底板的初始温度为环境温度，侧墙材料的初始温度设定为浇筑温度(25 ℃)；侧墙浇筑3 d后，拆除木模板，侧墙材料在浇水养护期间，其表面因风速影响，放热系数为1 296 kJ/(m2·d·℃)，木模板的对流系数为1 164 kJ/(m2·d·℃)。

1.1.4 普通侧墙模型再现及准确性验证

根据文献[11]的建模方法，采用ANSYS 18.2有限元分析软件对地下侧墙温度收缩应力进行分析。由于地下侧墙为对称结构，因此计算模型按照对称条件进行选取，即选取二分之一的侧墙进行温度收缩应力分析。规定沿地下侧墙墙体长度、高度和宽度方向分别为x轴、y轴和z轴，则侧墙的几何尺寸为 18 m × 4.2 m × 0.4 m，其中0.4 m高的墙体与基础底板一同浇注(即吊模段高0.4 m)，基础底板的几何尺寸为18 m × 1 m × 2.4 m。模型采用热-结构间接耦合计算的方式，分别选用 SOLID 70(热单元)与 SOLID 45(结构单元)，单元网格的划分长度为0.2 m。

将有限元模拟得出的温度收缩应力结果与弹性力学公式推导的结果进行对比，两者得出的规律具有一致性，且裂缝分布与实际工程相吻合。图2给出了侧墙模型验证，通过图2可知，本文再现的模型基本与文献[11]中的模型相吻合，本文再现模型的准确性得到验证。

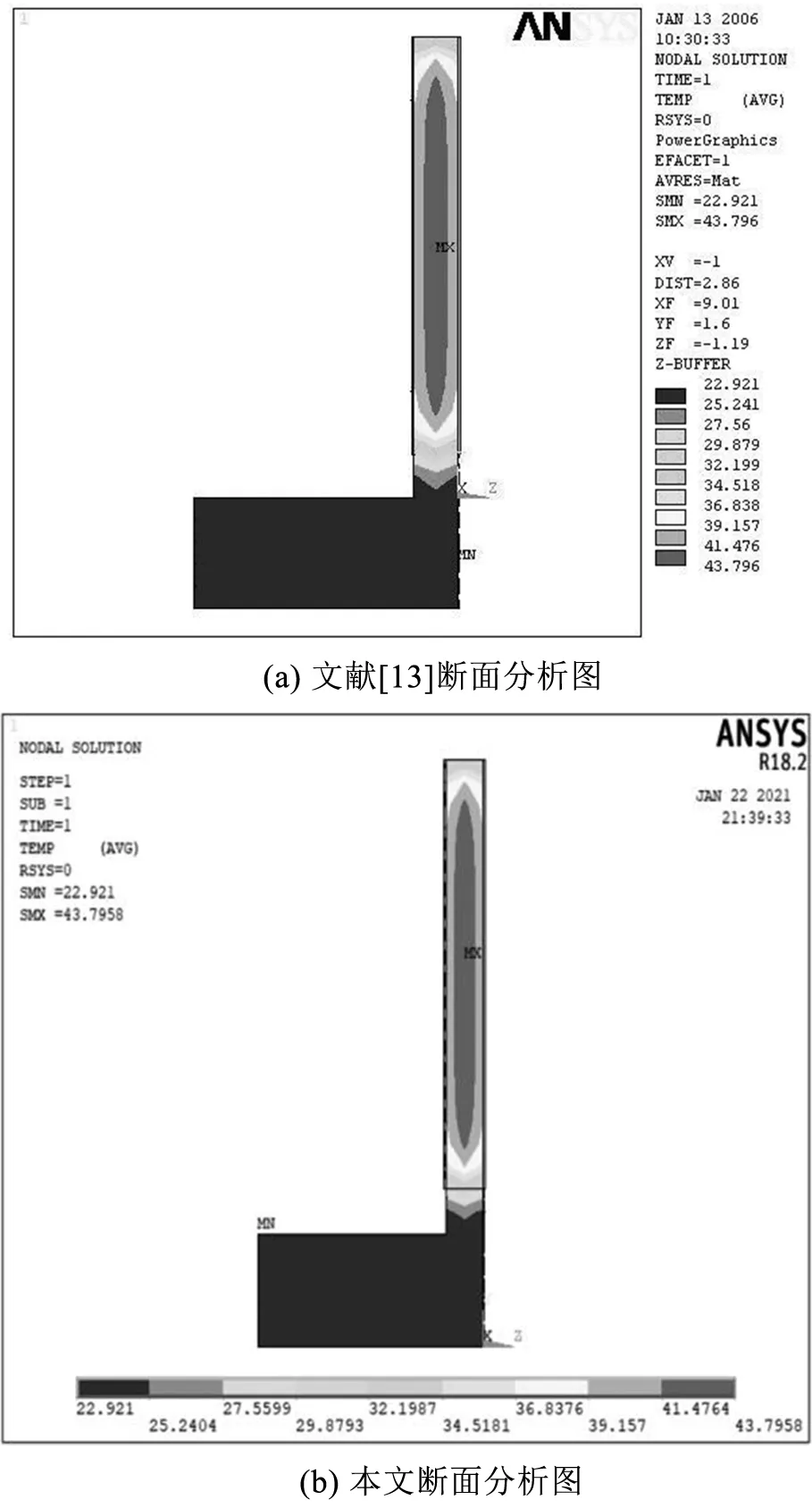
图2 侧墙模型验证

1.2 剑麻纤维-ECC地下侧墙模型建立

将再现模型中的普通混凝土材料参数换成剑麻纤维-ECC材料参数，具体参数见表1～表3，其他条件(侧墙尺寸、荷载选取、边界条件及初始条件等)均与普通侧墙相同，并在原有的基本假定处多加一条假定：对于剑麻纤维-ECC材料，不考虑剑麻纤维与水泥基之间的黏结滑移。最终，得到剑麻纤维-ECC新型地下侧墙模型。

2 地下侧墙温度场分析

2.1 剑麻纤维-ECC地下侧墙温度场变化规律分析

图3给出了剑麻纤维-ECC侧墙浇筑1 d后温度场示意图。以侧墙中央节点为代表性节点(x=0,y=3.3,z=-0.2)，绘制了该节点温度随龄期变化的关系曲线，见图4。

图3 剑麻纤维-ECC侧墙浇筑1 d后截面的温度场

图4 新型侧墙中央节点处温度-龄期关系曲线

由图3(a)可知，沿地下侧墙长度方向(即x方向)，在同一水平高度处，地下侧墙的温度基本没有发生改变。由图3(b)可知，沿地下侧墙厚度方向，侧墙中央位置处温度最高，侧墙内侧面与外侧面温度相对较低；沿侧墙高度方向，侧墙中央位置处温度最高，侧墙主体部分与吊模交接处、侧墙顶部温度相对较低。总的来说，因为地下侧墙较薄，所以温度沿墙体厚度方向的变化不大，墙体截面的温度等值线呈对称的椭圆状分布。

由图4可知，从剑麻纤维-ECC材料浇筑开始，剑麻纤维-ECC地下侧墙的温度场经历了温升、温降及趋于室温3个阶段。3个阶段的地下侧墙温度场变化规律如下：

(1)温升阶段：在地下侧墙浇筑后，剑麻纤维-ECC开始释放大量水化热，此时水化产生的热量大于散失的热量，使得剑麻纤维-ECC地下侧墙温度快速升高；由有限元温度场计算结果可知，剑麻纤维-ECC地下侧墙在2 d 时达到了最高温度(51.99 ℃)，在温度上升阶段，地下侧墙的中心温度受环境温度的影响并不明显。

(2)温降阶段：地下侧墙温度存在最高峰值，当到达最高峰值后侧墙温度开始下降，在第3 d拆模后，温降速率变快，此时剑麻纤维-ECC材料表面放热系数急剧增大，地下侧墙的温度受环境温度的影响较为明显。

(3)稳定阶段：随着时间的推进，侧墙水化热减小且墙体散失热量较多，最终侧墙温度趋于环境温度。

2.2 不同地下侧墙温度场的对比分析

以侧墙中央节点(x=0,y=3.3,z=-0.2)为代表性节点，将ANSYS计算得到的不同侧墙中央节点的各龄期温度值列于表4。

表4 剑麻纤维-ECC与普通C40混凝土地下侧墙中央节点的各龄期温度值对比

由表4可知，剑麻纤维-ECC地下侧墙温度峰值(52 ℃)较普通混凝土的温度峰值(43.8 ℃)高，且剑麻纤维-ECC地下侧墙出现温度峰值的时间(第2天)较普通混凝土侧墙温度峰值出现的时间(第1天)滞后。这是由于剑麻纤维-ECC属于轻质新型材料，其密度约为2 200 kg/m3，小于普通混凝土密度2 400 kg/m3，造成剑麻纤维-ECC地下侧墙绝热升温值高于普通混凝土侧墙；且剑麻纤维-ECC侧墙中水泥掺量多于普通混凝土侧墙，所以剑麻纤维-ECC地下侧墙水化热多于普通混凝土侧墙，而且剑麻纤维-ECC地下侧墙峰值温度要高于普通混凝土侧墙。此外，由于剑麻纤维-ECC的导热系数较普通混凝土小，较低的热传递率使得墙体保温效果较好，导致剑麻纤维-ECC地下侧墙温度峰值出现的时间较普通混凝土地下侧墙滞后。

3 地下侧墙应力场分析

3.1 剑麻纤维-ECC地下侧墙应力场变化规律分析

在实际工程中，地下侧墙出现的裂缝大多数是竖向裂缝。因此，对沿地下侧墙长度方向的正应力σx进行分析，图5给出了剑麻纤维-ECC侧墙浇筑1 d后应力场的示意图。为更加直观地分析地下侧墙应力场，绘制了剑麻纤维-ECC地下侧墙出现最大拉应力处节点(x=0,y=1.4,z=-0.2即节点2)的应力随龄期变化关系曲线，如图6所示。

图5 剑麻纤维-ECC侧墙浇筑1 d后应力场

由图6可知，地下侧墙的σx随着时间发生变化。温升阶段，侧墙因产生热膨胀导致墙体内部的σx基本是压应力(拉正压负)，最大的压应力值位于墙体中部的截面处；自墙体顶部向下，墙体顶面压应力较小，而底部的压应力大，这是由于与空气接触的墙体顶面和内外两侧面散热较快，其温度变化较小引起的。温降阶段，随着剑麻纤维-ECC地下侧墙出现收缩，侧墙内的压应力逐渐减小至零，发展到产生拉应力，且几乎所有σx全转为拉应力；沿侧墙长度方向，端部应力逐渐减小，墙体中间(即截面X=0处)产生应力最大值；沿墙体厚度方向，应力等值线呈对称的椭圆状分布，即中间部位拉应力大，两端墙面拉应力较小；沿墙体高度方向，墙体底部因受到基础底板约束，拉应力较大，墙体顶面应力则较小。

图6 节点2的应力-龄期关系曲线

3.2 不同地下侧墙应力场的对比分析

以侧墙出现最大拉应力处的节点(x=0,y=1.4,z=-0.2，即节点2)为代表性节点，将ANSYS计算得到的不同侧墙的节点2处各龄期温度收缩应力值列于表5。

由表5可知，剑麻纤维-ECC地下侧墙峰值拉应力(1.20 MPa)低于普通混凝土地下侧墙峰值拉应力(1.25 MPa)。产生的原因是：剑麻纤维-ECC的弹性模量(27.460 kN/mm2)明显低于普通混凝土弹性模量(32.500 kN/mm2)，材料的弹性模量小，能够产生较大的徐变，对于构件中受约束的水泥基材料，尤其是对初龄期水泥基材料，徐变能够松弛其大部分的拉应力，对降低地下侧墙早期开裂危险性起到极其重要的作用。对普通钢筋构件，侧墙的徐变能消除结构内部的温度收缩应力，减少结构的开裂现象；对预应力结构，侧墙的徐变会使预应力损失增加。

表5 剑麻纤维-ECC与普通C40混凝土地下侧墙节点2处各龄期温度收缩应力值对比

图7给出了节点2各龄期的应力与材料抗拉强度的关系曲线，不同侧墙材料各龄期的抗拉强度值分别列于表6。

表6 剑麻纤维-ECC与普通C40混凝土各龄期的抗拉强度值对比

图7 节点2各龄期的应力与材料抗拉强度关系曲线

由图7可知，当侧墙节点应力曲线低于材料抗拉强度曲线时，地下侧墙不开裂；当侧墙节点应力曲线与材料抗拉强度曲线相交时，在交点对应时刻地下侧墙开裂。可见，在相同施工条件下，采用普通混凝土的地下侧墙发生了开裂，采用剑麻纤维-ECC的地下侧墙不开裂；将剑麻纤维-ECC材料用于地下侧墙结构时，其控裂性能要好于普通C40混凝土，能够减小地下侧墙的开裂风险。

3.3 剑麻纤维-ECC地下侧墙根据环境温度不同的施工优化

在实际工程中，随着地下侧墙浇筑的季节不同，侧墙所处的环境温度有所不同，而在不同的环境温度下，剑麻纤维-ECC地下侧墙的控裂情况可能会发生改变，本文分析了不同环境温度对剑麻纤维-ECC地下侧墙温度收缩应力的影响。进行有限元分析时，除环境温度外，地下侧墙的其它热力学条件与约束条件都保持不变，将环境温度分别设置为15、25、35 ℃，从而得到不同环境温度下地下侧墙温度收缩应力随时间变化关系曲线，见图8。

图8 节点2应力随龄期变化曲线

由图8(a)可知，在环境温度较低时(15 ℃)，地下侧墙会因降温速率较快，形成较大的拉应力，造成地下侧墙开裂；由图8(b)可知，为降低剑麻纤维-ECC地下侧墙的开裂风险，对该环境温度下的剑麻纤维-ECC地下侧墙可采用降低入模温度的施工优化方法。

4 结论

1)从浇筑材料开始，剑麻纤维-ECC地下侧墙温度场经历了温升、温降及趋于室温3个阶段；在剑麻纤维-ECC水化热引起的温度上升阶段，由于材料受热膨胀，墙体内部产生压应力，之后，随着侧墙温度降低，剑麻纤维-ECC开始收缩，墙体内的压应力逐渐减小至零，并发展到产生拉应力。

2)与普通混凝土相比，剑麻纤维-ECC材料密度小、水泥掺量多、导热系数小，因此剑麻纤维-ECC地下侧墙温度峰值较普通混凝土地下侧墙的温度峰值高，且出现温度峰值的时间较普通混凝土侧墙滞后。

3)剑麻纤维-ECC的低弹模特性能够有效控制地下侧墙早期裂缝的产生；将剑麻纤维-ECC材料用于地下侧墙结构时，其控裂性能要好于普通C40混凝土，能够减小地下侧墙的开裂风险。

4)在环境温度较低时，地下侧墙会因降温速率较快，形成较大的拉应力，造成地下侧墙开裂；为降低剑麻纤维-ECC地下侧墙的开裂风险，可采用降低入模温度的施工优化方法。