基于小波包变换及互相关的古建木材声发射源定位研究★

周占学，黄晓峥，梁玉国，曹玉红，徐永峰

(1.河北建筑工程学院,河北 张家口 075000; 2.河北省土木工程诊断改造与抗灾重点实验室,河北 张家口 075000; 3.河北省建筑科学研究院有限公司,河北 石家庄 050000)

0 引言

我国古建筑多以木结构形式存在,其主要承重构件因遭遇数千年气候变化或人为因素影响后,内部产生缺陷或损伤,如不及时进行检测并对损伤位置进行补救,就会随时面临坍塌、破坏等危险,因此,获取准确的损伤源位置对古建保护具有重要意义。声发射(Acoustic Emission,AE)技术作为一种动态无损检测技术,可以对结构损伤过程进行检测并可以快速、准确地发现损伤的位置。目前,常用的AE定位方法为时差定位法,即通过信号在各传感器之间传播的时差来对AE源进行定位[1],时差的准确与否直接影响着定位的精度。声发射信号到达各传感器的先后时间称为时间延迟[2],在木材AE源定位中常用的时延估计法有阈值法、峰值分析法、自适应时延估计以及信号互相关分析法[3]。申珂楠等[4]采用小波分析对声发射信号降噪,并提出了基于最大值时差法测速的AE源三角定位法。李晓崧等[5]基于信号相似度小波重构算法以胶合木为研究对象提出一种新的时差定位算法。张高品等[6]根据应力波在木材内的传播时间基于小波变换和时延估计提高了木材内部缺陷的识别精度。鞠双等[7]采用断铅试验并应用小波变换和相关性分析对马尾松胶合木表面声发射信号各向异性传播规律进行了研究。

本文采用声发射设备对断铅点进行数据采样,基于小波包分解重构和互相关技术研究古建木材声发射信号时延估计,实现了对木材损伤源的定位,在有效抑制噪声的基础上达到了无损检测的目的,有效提高了声发射源的定位精度。

1 基于小波包变换的广义互相关时延估计方法

1.1 小波包分解重构原理

小波包分解是在小波分解的基础上提出的,其基本思想是集中所有可能发生的信息能量,筛选出信号的有序性,因此,小波包分解相比小波分解更加精密、准确[8]。小波包分解是对原始信号进行二分法逐级分解即原始信号通过低通滤波器得到近似系数,通过高通滤波器得到细节系数,将第一层的近似系数作为信号输入,又得到一组近似系数和细节系数;再将得到的近似系数作为信号输入得到第二层的近似系数和细节系数;以此类推直到满足设定的分级等级[9]。本文选用Daubechies小波作为小波基函数结合采样频率对信号进行五层小波包分解,其分解后树状结构图如图1所示。

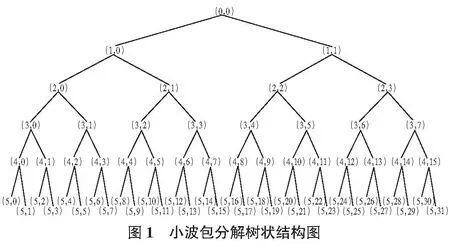
如图1所示,信号经过小波包N层分解后会得到2N个小波包,分解得到的各个小波包代表信号包含的各个频率段,每分解一次小波包得到的信号点数相比于上一层减少一半,即分解层数越多,频域分辨率越高,时域分辨率越低。为提高时域分辨率,采用小波包重构算法,将重构的小波包提取,其他小波包用零填充,并代入重构公式:

(1)

1.2 互相关分析

假设x0处存在声发射源,x(t)和y(t)分别为两处传感器接收到的声发射波形信号,Rxy(τ)表示两个声发射信号的相关程度,则信号x(t)和y(t)的互相关函数即可表示为式(2):

(2)

其中,T为采集时间;τ为时移量。

其估值为:

(3)

互相关函数描述的是两个信号之间的依赖关系,根据互相关函数定义可知,两个函数相关程度最大时,则互相关系数|Rxy(τ0)|达到最大,假设其最大值所对应的时延为τ0,即当信号y(t)沿时间轴平移τ0个单位时,两个信号相似程度达到最大,进而通过互相关函数间接确定声发射源的位置。

由于互相关函数数值大小不能表示两个变量函数的相关程度,因此实际分析中一般采用互相关系数表示,其表达式见式(4):

(4)

当|pxy(τ)|越接近于1时,表明信号之间具有越高的相似性,|pxy(τ)|在最大值处所对应的时差即为两处传感器接收到的信号时差。因此,可以通过计算互相关系数达到最大值所对应的时差,达到精位的目的。

1.3 时延估计定位

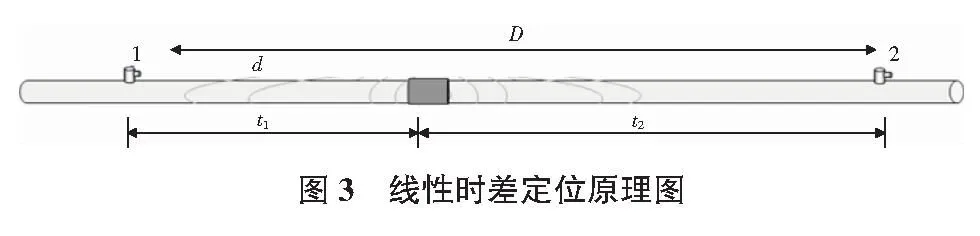
当被测物体长度和半径之比非常大时,如管道、棒材、钢梁等可以采用一维时差定位进行声源的确定。考虑到被检测木材的长度和半径比很大,可以看作线条材料,因而本文定位试验采用线性时差定位。线性时差定位法要求至少设置两个传感器,假设声源处于两个传感器之间,其中传感器1接收到的信号时间为t1,传感器2接收到的信号时间为t2,由此可以得到信号到达两个传感器的时差为Δt=t2-t1,将计算得到的时差Δt代入时差定位公式即可得到声发射源到传感器的距离,将两个传感器的间距表示为D,声源产生的波传播速度表示为v,则声发射源距离1号传感器的距离可表示为式(5)[10]:

(5)

其中,D为两个传感器之间的距离;v为声发射信号在木材中的传播速度;d为声发射源距离传感器的位置距离;Δt为基于小波包变换互相关分析得到的时差。

2 材料与试验方法

2.1 试验材料与设备

试验选取的材料为张家口市万全区某乡村收集传统木结构建筑拆除下来的绝干松木梁,其径长为320 mm,声发射监测系统采用由北京软岛科技有限公司生产的DS5系列全波形声发射信号分析仪,采样频率设定为2.5 MHz,传感器型号为RS-2A型,前置放大器增益为40 dB。

2.2 声速标定

首先在进行声发射定位试验之前,需要对声发射信号在构件中的传播速度进行设置,不同的木材构件内部结构不同,具有很大的差异性,为避免其他因素的干扰,应针对具体试验对象测定声发射信号在构件中的传播速度。本节通过断铅试验的方法对木梁完成了波速的测定,将计算得到的波速平均处理,从而有效减少了因传播速度差异较大对定位精度的影响。

根据传感器最大间距布置规则,通过多次试验,在时差定位中,最大传感器间距对应的传播衰减值不宜大于木材断裂声发射信号对应的幅值和采样门槛值对应的幅值之差,当声发射信号传播至3号传感器之前,声发射幅值都大于试验设定的40 dB门槛值,直至3号传感器之后,声发射幅值逐渐低于设定阈值,同时根据试验木梁上断铅模拟木材断裂产生的声发射信号幅值主要集中在98 dB左右,因此,两个传感器衰减值都不得高于58 dB。综上,本文将1号传感器平均幅值98.6 dB衰减至3号传感器平均幅值48.2 dB,平均幅值衰减量达到50.4 dB时所对应的传播距离600 mm作为本次定位试验的定位间距。

在木梁表面相距600 mm处放置1号和3号传感器,在1号传感器和3号传感器附近各断铅10次,断铅示意图如图2所示,根据两传感器之间的距离及信号到达两传感器的时间差,计算得到断铅信号在木梁构件中的传播速度。

将两传感器测得的时差进行统计,并根据距离计算得到的声发射信号传播速度数据如表1所示。

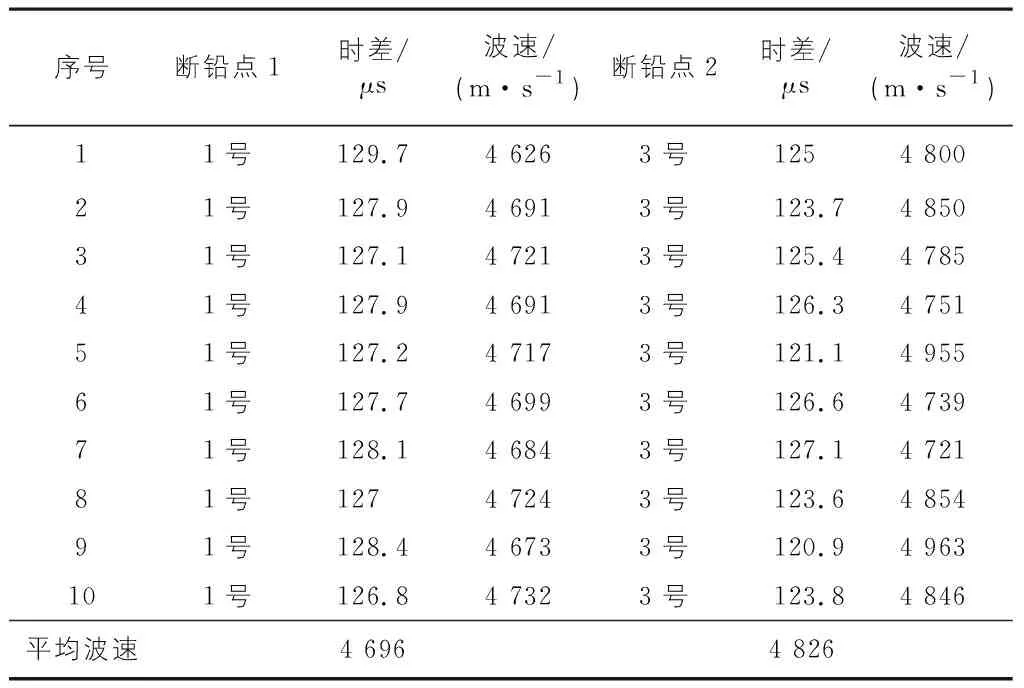
表1 声速标定测量结果

根据表1可知,在其他系统参数不变,只改变声波的传播方向时,1号传感器测算出来的波速总是小于3号传感器测算出来的波速,且每次断铅测得的波速在大小上存在差异,由此说明声发射信号在木材构件中传播的各相异性,每次断铅时,声发射信号受到木材构件内部结构的影响使得传播距离发生改变,从而使得波速产生变化。因此,基于上述两个方向测得的平均波速,并将两个方向平均波速折中处理,取平均波速4 761 m/s作为本文声发射源定位试验的传播速度。

2.3 断铅定位试验

时差定位原理图如图3所示,由式(5)可以得出,当AE源在两传感器中间时,此时Δt=0;当AE源靠近1号传感器时,此时Δt=D/v;当AE源靠近2号传感器位置时,此时Δt=-D/v,由此可知,损伤源的定位精度在于时差Δt和传播速度v的精确程度,由于在试验开始前已对被测构件进行了多次声速测试且两个传感器距离很近,从而有效避免和减少了波速对试验定位精度的影响。因而,在已知波速v和传感器间距D的情况下,时差Δt影响着定位精度。

由于实际木材在损伤断裂过程中同时产生多个AE源且不易区分,因此采用铅芯在木梁表面折断的方式模拟木材破坏产生的单个损伤源,如图4所示。参照国外标准ASTM-E976测定声发射传感器响应再现性的标准指南[11],将一个铅芯直径为0.5 mm的自动铅笔放在试验材料表面成30°折断进行断铅试验。

保持两传感器有效传播距离为600 mm不变,为保证损伤位置的随机性和试验结果的可靠性,分别在距离1号传感器100 mm,200 mm和450 mm位置处进行断铅,在同一断铅点重复5次断铅,共采集15次实验数据,最后根据采集的试验数据和波形进行处理,并根据AE信号讨论不同时差定位方法对损伤源时差和位置精度的影响,得出一种定位精度更高的损伤定位方法,传感器布置及定位原理如图5所示。

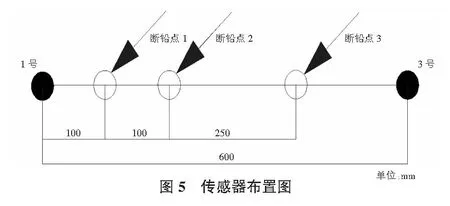
从图5可以看出,两传感器位置间距为600 mm,以1号传感器为坐标原点和3号传感器构成的直线方向为正向进行声源定位,则1号传感器坐标为(0,0),3号传感器坐标为(600,0);断铅点1位置坐标为(100,0),断铅点2位置坐标为(200,0),断铅点3位置坐标为(450,0)。经多次声速标定取平均值得到木材中的传播速度为4 761 m/s,对各试验数据经过小波包分解重构后进行互相关分析,从而得到1号传感器和3号传感器的时差,代入时差定位公式即可得到声发射源损伤位置。

3 试验结果分析

经多次试验,以优化数据压缩并减少噪声为目的。选取具有较高消失矩阶数的Daubechies小波(db3)为基函数对声发射信号进行5层小波包分解,以3号传感器在断铅点1接收的声发射信号为例,其分解得到的前8个节点对应的频谱如图6所示。

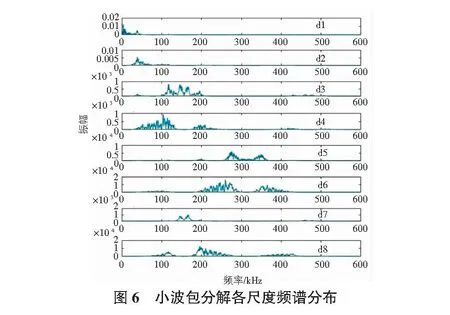
根据相关文献,木材AE信号主要集中于50 kHz～200 kHz[12],从图6可以看出,第2,3,4,7层信号频率主要集中在50 kHz～200 kHz,其在第3层以后信号振幅很小,因而对上述4层信号进行重构,其波形如图7所示。

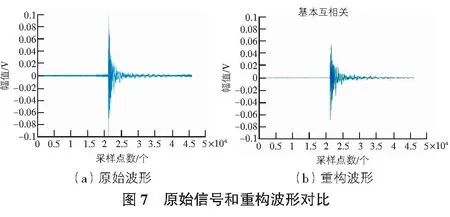
从图7可以看出,经重构后的信号波形包含了原始波形的变化趋势,去除了原始信号中大部分噪声,同样对其他声发射信号进行处理,信号保留了原始信号的波形变换且去噪效果良好。将通道1和通道3重构后的声发射信号进行互相关分析,如图8所示。

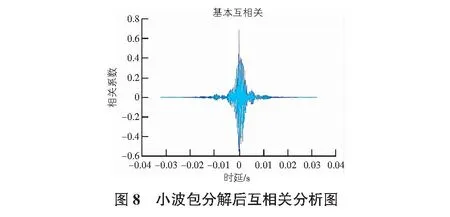
综上可知,两传感器接收到的声发射信号具有较好的相关性,在Matlab中利用互相关程序得到互相关系数在0.754处达到最大值,其最大值所对应的0.41×10-4s=41 μs,将时差代入式(5)即可求得AE源的位置。同理将其他断铅点的声发射信号经小波包分解重构后进行相关分析得到断铅点位置和预设点位置如表2所示。

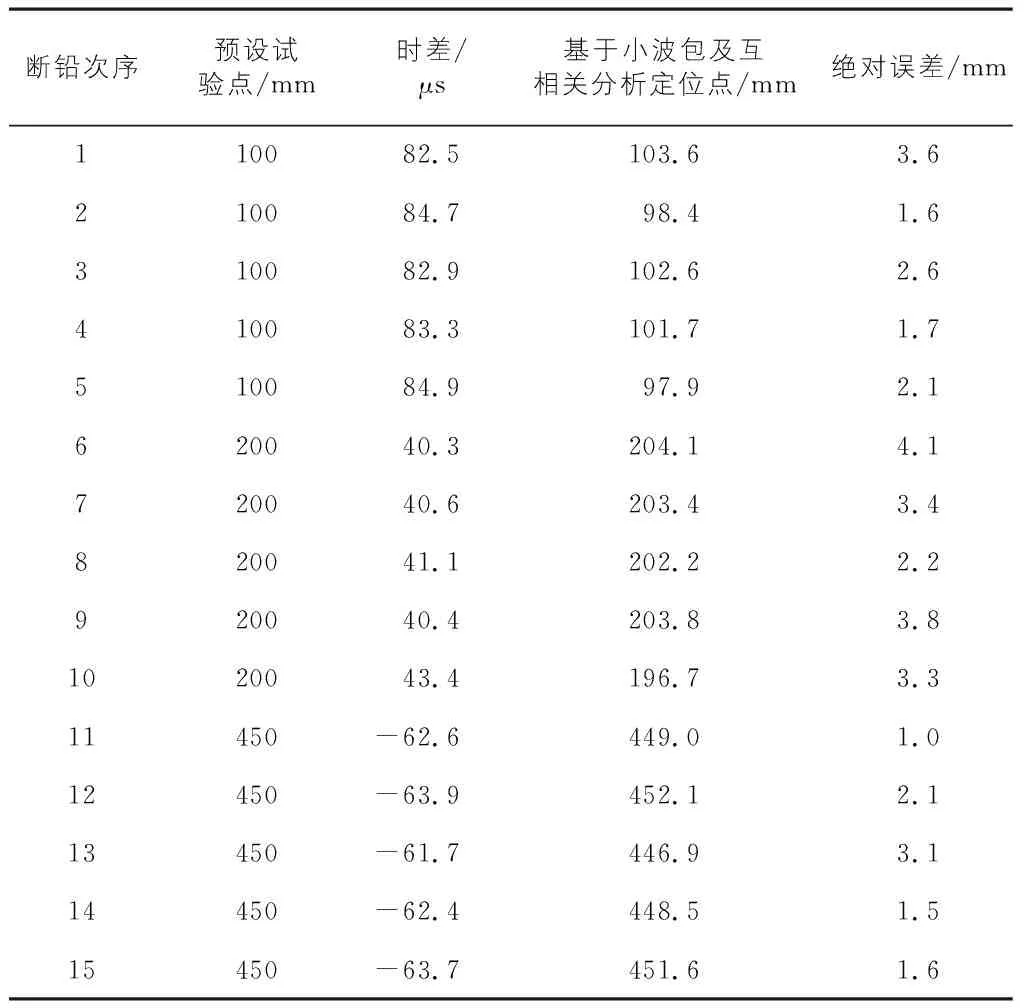
表2 基于小波包分解及互相关定位结果和预设试验点比较

从表1可以看出,三种不同位置处断铅得到的声发射源定位结果与预设试验点位置相差很小,在断铅点1处平均误差在2.3 mm;断铅点2处平均误差在3.4 mm;断铅点3处平均误差在1.9 mm,平均定位误差都在5 mm以内。因此,基于小波包及互相关的声发射源定位方法有效的提高了定位精度,从而为古建损伤定位检测提供新思路和途径。为进一步对比三种不同定位方法之间的定位效果,分别将系统自带定位方法、互相关分析定位方法和小波包-互相关函数定位方法记为A,B,C,相对误差分别记为δA,δB,δC,分别将各定位结果产生的时差与理论时差作比,得出相对误差值,结果如表3—表5所示。

表3 100 mm处信号相对误差对比表

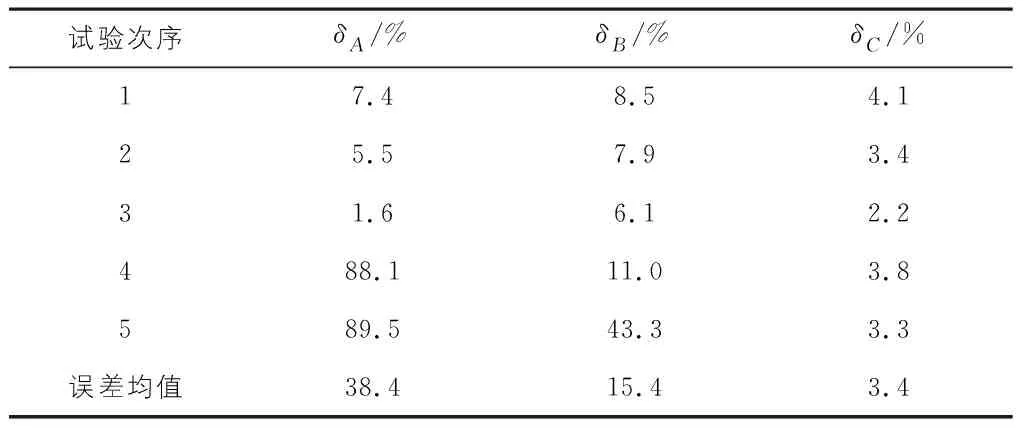
表4 200 mm处信号相对误差对比表

表5 450 mm处信号相对误差对比表

由表3—表5可以看出,在不同断铅位置处分析得到的定位误差具有一定的相似规律,同时不同定位方法得到的定位误差具有一定的差异性。以100 mm位置处断铅试验结果为例,三种定位方法δA,δB,δC得到的相对误差分别为7.8%,5.1%,1.2%,对比δA和δB,传统定位方法得到的平均相对误差为7.8%,互相关函数得到的平均误差为5.1%,定位精度有了一定的提升,说明互相关函数分析相比于传统阈值定位方法一定程度上可以提高损伤源的定位精度;对比δB和δC可以看出,经小波包降噪分解后,再进行互相关函数分析得到的相对定位误差为1.2%,定位精度有了明显的提升,从而说明经小波包分解变换后,并将特定频带的小波包系数进行互相关分析,可以有效地剔除原始AE信号中的噪声信号,并得到更小的定位误差结果,从而提高定位精度,此外,对比其他断铅位置的定位结果同样具有相似规律。

4 结论

针对古建木材声发射无损检测中损伤源定位精度不高的问题,采用小波包分解重构有效地降低了噪声对声发射信号的影响,然后对重构信号进行互相关分析得到两传感器AE信号的时差,进而通过时差定位对损伤源进行定位计算。试验结果表明:该方法极大保留了原信号的声发射特性,降低了噪声对损伤源定位的干扰,定位精度平均误差在5 mm以内,有效提高了声发射源定位精度,为古建木结构声发射源定位提供了一种新的方法。