基于改进粒子群算法的阻尼惯量自适应控制策略
卢盛阳,朱 钰,陈 涛,王 同,王 宁,吴 蒙
(1.沈阳工业大学电气工程学院,沈阳 110870;2.国网辽宁省电力有限公司电力科学研究院,沈阳 110006;3.大连理工大学电气工程学院,大连 116081)
伴随“双碳”目标计划的提出,电网逐渐呈现以“高比例新能源、高比例电力电子设备”为主的“双高”特性。由于新能源具有波动性、间歇性等特点,故需对电源侧及负荷侧进行双向调整,并对现有电力系统提出较高要求[1]。新能源并网主要利用逆变器装置,但其并不具备与同步发电机类似的惯量与阻尼特性,当新能源大规模并网,会导致电力系统阻尼与惯量不足,严重时导致电力系统产生频率崩溃[2-3]。
为解决上述问题,虚拟同步发电机VSG(virtual synchronous generator)技术应运而生。目前针对VSG 的理论研究,主要集中于VSG 模型建立[4-5]、系统稳定性分析[6-7]、储能VSG[8-9]建模及VSG 参数设计[10-11]等问题。由于VSG技术主要完成同步发电机的惯量与阻尼特性的模拟,虚拟惯量与阻尼系数是VSG控制策略的核心参数,对其进行适当调整可有效提升VSG 的控制性能。但当前研究主要将VSG的虚拟惯量及阻尼系数设为恒定,使研究具有较大的局限性,因此对阻尼惯量参数优化展开研究具有必要性。如何调整系统参数以使动态性能及稳定性提高成为当下研究热点,文献[12]为改善系统动态性能提出一种虚拟惯量自适应VSG控制策略,却未考虑阻尼系数与系统稳定性的关联;文献[13]在此基础上提出自适应阻尼惯量控制策略,但该方法未结合稳定性分析。由以上分析可知,现有研究虽优化了系统的动态性能及稳定性,但仍存在较多不足,使传统参数计算过程较为繁琐,VSG 控制策略的整体控制效果较差。
综上所述,本文选取系统输出角频率偏移为优化目标,结合改进粒子群算法优化VSG 参数,提出一种阻尼惯量自适应控制策略调整系统的虚拟惯量及阻尼系数,旨在优化系统动态响应及暂态稳定性。
1 VSG 基本原理
1.1 VSG 模型
VSG 典型拓扑结构如图1 所示,通过采集主电路输出电压及电流,获得功率,经过功率环及电压电流双闭环控制产生调制波,并将其传送到对应逆变器。
图1 中,Vdc为直流电源;C为滤波电容;V1~V6为开关管;L、C1分别为滤波电感和电容;L1、R为线路电感和电阻;ug为电网电压;uoabc为逆变器输出三相电压;igabc为逆变器输出三相电流;iabc为流经电感L的三相电流。
VSG的转子运动方程可表示为
式中:Pm、Pe分别为VSG 系统输入机械功率及电磁功率;J为虚拟惯量;D为阻尼系数;ω为系统运行时角频率;ωn为转子参考角频率。
1.2 VSG 动态特性分析
VSG并网等效电路如图2所示。图2中,E为三相并网逆变器输出电压的有效值;定义Z=R+jXs,Z为三相并网逆变器输出阻抗与电网阻抗之和,R为阻性分量,Xs为感性分量;δ为三相逆变器输出相位角与电网相位角偏移,即
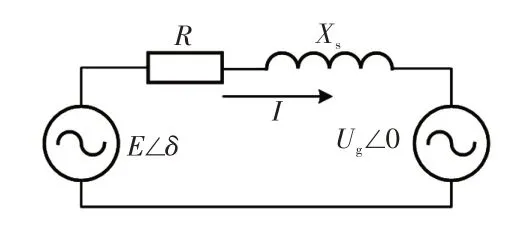
图2 VSG 并网等效电路Fig.2 VSG grid-connected equivalent circuit
由于逆变器输出电压与电网电压间的阻抗一般为感性,则并网逆变器馈入电网时的有功功率为
结合式(1)~(3),可得VSG 系统的有功功率控制环的闭环控制框图如图3所示。
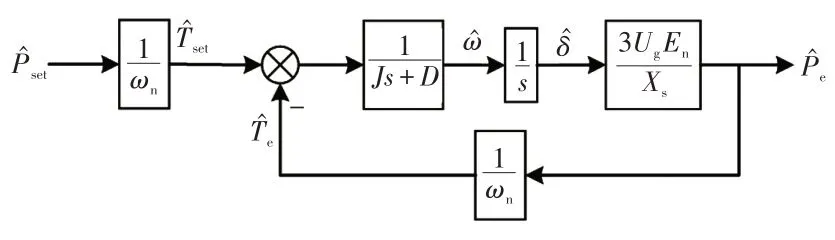
图3 VSG 有功功率控制框图Fig.3 Block diagram of active power control of VSG
由式(4)可得自然振荡频率ωs及阻尼比ξ为
由式(5)可知,系统的自然振荡频率ωs及阻尼比ξ与虚拟惯量J、阻尼系数D有关,而ωs与ξ直接决定二阶时域系统的时间响应。因此,虚拟惯量J及阻尼系数D对系统输出响应有较大影响。
2 改进粒子群算法
2.1 适应度函数设计
适应度函数是用于对种群个体的适应性进行度量的函数[14]。误差绝对值时间积分ITAE(integrated time absolute error)作为一种控制系统性能评价指标,常被用于全面描述系统的动态性能,故本文采用ITAE作为优化目标,并选取系统输出角频率偏移作为反映系统性能的指标。ITAE的表达式为
式中,e(t)为输出误差。
根据式(1)中所述的同步发电机转子运动方程,将其视为以ω为变量的微分方程,可解得
由式(6)、(7)可得适应度函数表达式为
式中,Fitness为该粒子的适应度函数值。
2.2 粒子群算法的改进
2.2.1 惯性权重的改进
惯性权重w为粒子惯性,实际优化过程中,前期希望粒子具有较好全局搜索能力,即前期惯性权重取值应较大;后期具有较好局部搜索能力,故此时权重取值应减小。利用自适应惯性权重更新公式代替固定惯性权重,自适应惯性权重更新公式可表示为
式中:wmin、wmax分别为预设最小与最大的惯性权重,一般wmin取0.4、wmax取0.9;为第d次迭代时所有粒子的平均适应度;f()为第d次迭代时第i个粒子适应度;为第d次迭代时所有粒子的最小适应度;为第d次迭代时第i个粒子惯性权重。
2.2.2 引入耦合中心游移及边界邻域更新策略
1)耦合中心游移策略
粒子群算法虽能够快速收敛,但易出现种群个体质量低、易陷入局部最优等问题[15],对立学习策略可有效解决这一问题。引入中心游移公式偏移初始解,可多点同步搜索粒子最优位置,以便于进一步提升种群的多样性[16]。
耦合中心游移的初始化策略可表示为
式中:为第t次迭代时生成的第i个个体;uup为寻优空间上限;udown为寻优空间下限;为第t次迭代时的初始解;为中心游移在第t次迭代时生成的第i个个体;μ为中心游移系数,μ=0.618。
2)边界邻域更新策略
大量实验证明,在粒子飞行寻求最优解的过程中,粒子会存在飞越边界现象,故待优化问题最优解通常难以获取[17]。针对上述问题,通过引入边界邻域更新策略修正越界粒子位置,该策略具体修正公式为
式中,U为在某一区间上的均匀分布。
3 VSG 阻尼惯量自适应控制策略
基于VSG动态特性可知,调整系统的虚拟惯量及阻尼系数可改善系统的阻尼比,进而改善系统动态性能。本节基于系统稳定性约束条件,设计一种VSG阻尼惯量自适应控制策略。
3.1 初始参数确定
由图3可得系统的开环传递函数为
由式(13)可知,G(s)主要由3个环节构成,由于含有一阶低通滤波环节,故在截止频率处,环路增益的幅值为1,即
式中,fc为截止频率。
由式(13)及(14)可得系统的虚拟惯量为
为使式(15)成立,则
式中,fcmax为截止频率最大值。
可得阻尼系数为
由于VSG是利用逆变器模拟同步发电机特性,而实现精确模拟的前提即是内环控制器的动态响应要足够快,故系统的特征根应与虚轴之间有一定的距离以保证控制性能且满足系统的稳定裕度,则
式中,Re(s)max为系统特征根的最大值。
基于以上分析可得在考虑系统稳定性的情况下,虚拟惯量J及阻尼系数D的取值范围为
3.2 阻尼惯量自适应控制策略
在系统产生扰动时,系统的角频率随时间的变化情况如图4 所示。可根据系统的角频率偏移及角频率变化率对系统的虚拟惯量及阻尼系数进行实时调整。
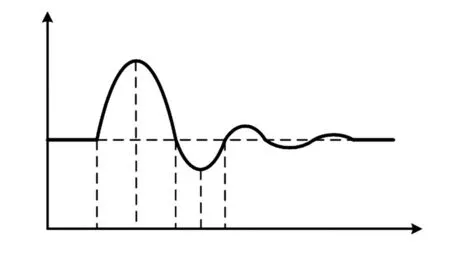
图4 VSG 角频率变化Fig.4 Changes in angular frequency of VSG
由图4 的系统角频率变化曲线可知,在系统达到稳态运行点前,系统角频率振荡可分为4 个区间。在区间t1~t2中,VSG 系统输出虚拟角频率大于电网角频率且处于增加趋势,此时角频率的变化率dω/dt先突然增加后又逐渐减小,故此时应增大虚拟惯量及阻尼系数以抑制dω/dt的增加;在区间t2~t3中,角频率的变化率dω/dt<0,此时系统角频率虽降低,但仍大于电网角频率,故应采用较小的虚拟惯量以加快角频率恢复至额定值,同时应增大阻尼系数以抑制角频率偏移量的超调;而在区间t3~t4及t4~t5中,系统的虚拟惯量及阻尼系数的选取原则与区间t1~t2及t2~t3一致,故本文不再赘述。
由以上分析可得,在不同条件下,VSG 系统的虚拟惯量J及阻尼系数D的取值如表1所示。
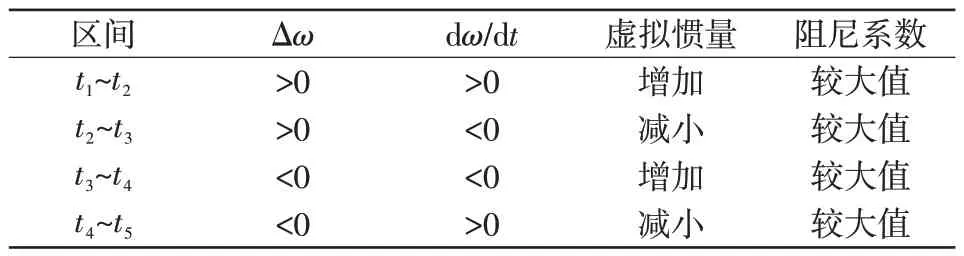
表1 虚拟惯量J 及阻尼系数D 的选取原则Tab.1 Selection principle for virtual inertia J and damping coefficient D
根据表1 中虚拟惯量和阻尼系数的选取原则及其与转子角频率变化率dω/dt及转子角频率偏移量Δω间的相关性,本文提出自适应控制策略为
式中:J0、D0分别为VSG 系统未受扰动时的虚拟惯量及阻尼系数,其取值通过第2.2 节所述改进粒子群算法求出;kJ、kD分别为VSG系统受扰动时虚拟惯量J及阻尼系数D的调节系数;α、β分别为虚拟惯量J及阻尼系数D的指数调节系数;Jmin、Jmax、Dmin和Dmax分别为考虑系统稳定性时虚拟惯量及阻尼系数的取值范围;T1、T2为自适应策略启动的阈值。
4 仿真分析
4.1 参数设置
为验证第1.2节理论及本文所提出的控制策略的优越性,基于Matlab/Simulink 仿真平台搭建VSG仿真模型,其主电路采用图1 的拓扑结构,参数设置如表2所示。
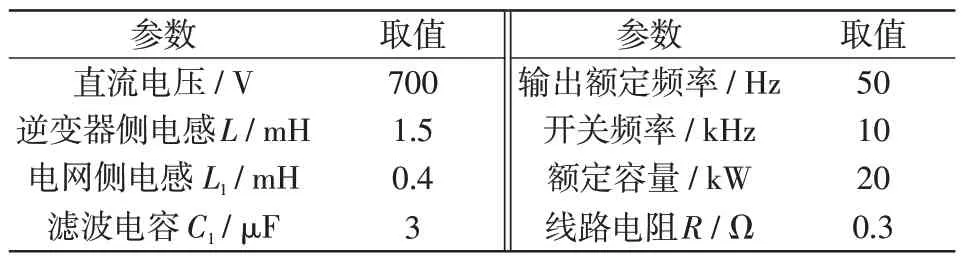
表2 仿真参数Tab.2 Simulation parameters
4.2 仿真分析
4.2.1 对比方案
选取恒定参数VSG 控制策略和常规阻尼惯量自适应控制策略作为对比方案,为便于比较控制效果,3种仿真模型均采用表2中的相关参数。
自适应VSG控制策略的核心公式可表示为
4.2.2 改进粒子群算法测试
图5 为适应度函数曲线,选取单模态基准函数为测试函数,对粒子群算法及改进粒子群算法进行测试,迭代次数均为300次。由图5可以看出,粒子群算法及本文提出的改进粒子群算法均能有效收敛,而改进粒子群算法的寻优速度优于粒子群算法,证明本文所提出的改进粒子群算法具有更好收敛性。
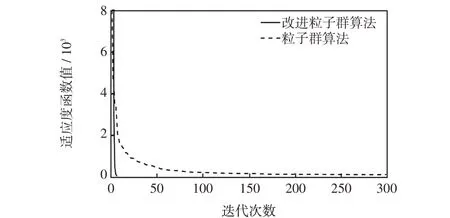
图5 适应度函数Fig.5 Fitness function
4.2.3 不同惯量及阻尼对系统影响
仿真时长设为2 s,假定初始系统处于稳定状态,VSG系统正常稳定运行时给定功率为10 kW,1 s时系统给定功率突增5 kW。
图6 为阻尼恒定、惯量变化时系统的输出角频率偏移及角频率变化率曲线。由图6可以看出,当系统虚拟惯量增大时系统输出角频率偏移超调减小,角频率变化率趋于振荡,动态性能变差,故虚拟惯量J增大可抑制系统频率超调,但使系统稳态调节时间增大。图7为在阻尼恒定、惯量变化下系统输出有功功率的变化曲线。由图7可以看出,当阻尼系数D恒定,虚拟惯量J增大时,系统输出有功功率超调量会增大,稳态恢复时间变长。
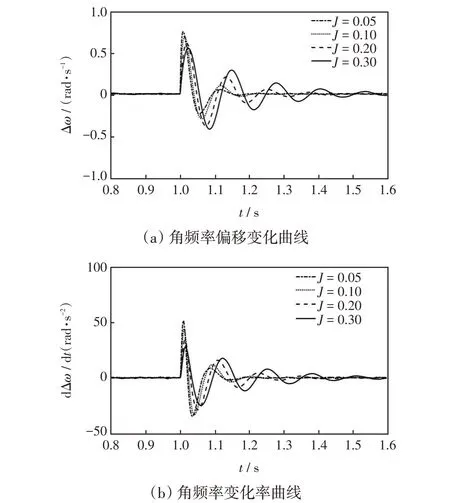
图6 不同虚拟惯量下角频率变化Fig.6 Changes in angular frequency under different values of virtual inertia
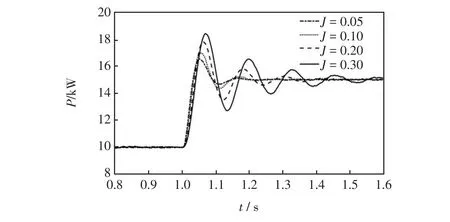
图7 不同虚拟惯量下有功功率变化曲线Fig.7 Curve of active power under different values of virtual inertia
图8 为在惯量恒定、阻尼变化下系统输出有功功率的变化曲线。由图8 可以看出,当虚拟惯量J恒定,阻尼系数D增大,系统输出有功功率超调量减小,调节时间缩短,故阻尼系数D对于有功功率的主要作用为加快系统调节时间,减小输出响应超调。图9为在惯量恒定、阻尼变化下系统输出角频率偏移及角频率变化率曲线。由图9可以看出,当阻尼系数D增大时,系统输出角频率超调减小,峰值时间缩短,稳态调节时间缩短,故阻尼系数D对系统频率的影响为减小系统缓冲时间,加快系统稳定。
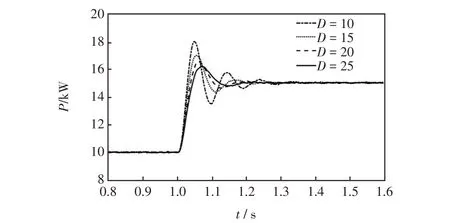
图8 不同阻尼系数下有功功率变化曲线Fig.8 Curve of active power under different values of damping coefficient
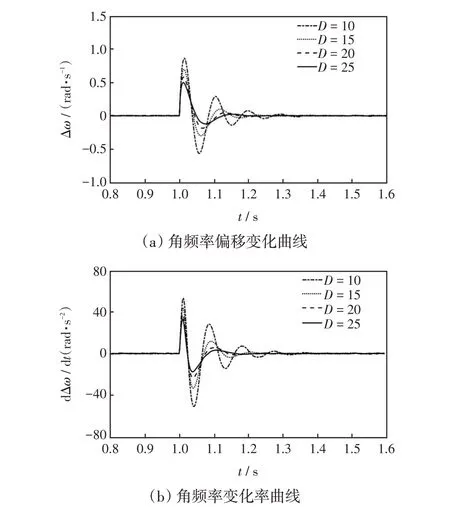
图9 不同阻尼系数下角频率变化Fig.9 Changes in angular frequency under different values of damping coefficient
基于以上分析可知,虚拟惯量J及阻尼系数D的变化均会对系统的稳定性及动态性能指标产生较大影响,且产生的影响效果与第1.2 节理论分析一致,但其取值并不是过小或过大为最好,需综合考虑系统实时变化情况。
4.2.4 VSG 阻尼惯量自适应控制仿真
仿真工况与第4.2.3 节一致,为验证本文所提控制策略优越性,与其余控制策略进行对比,模型参数设置与第4.1 节中参数设置相同。图10 为不同控制策略下系统输出角频率偏移曲线。由图10可以看出,采用常规VSG 控制即恒定参数控制策略,其角频率最大偏移量为1.26 rad/s,需经历约0.36 s 可恢复至稳态;采用常规J、D自适应控制策略,角频率最大偏移量为0.91 rad/s,调节时间为0.35 s,相较于恒定参数控制策略其动态性能指标有较为明显提升;采用本文所提出的阻尼惯量自适应控制策略,角频率最大偏移量为0.61 rad/s,且调节时间缩短至0.32 s。故本文所提出的策略可有效提升系统动态性能,并有利于系统稳定。
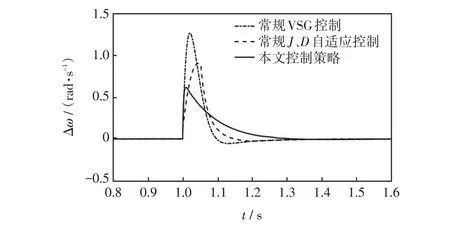
图10 不同控制策略下系统角频率偏移Fig.10 System angular frequency deviation under different control strategies
图11为系统输出有功功率曲线。由图11可以看出,采用常规VSG 控制即恒定参数控制策略,其功率波动的最大超调量为201.5 W,需经历约0.43 s才可恢复稳态;采用常规J、D自适应控制策略,功率的最大偏移量约为73.8 W,调节时间为0.39 s;采用本文所提出的阻尼惯量自适应控制策略,功率最大超调量为50.3 W,且调节时间缩短至0.32 s。
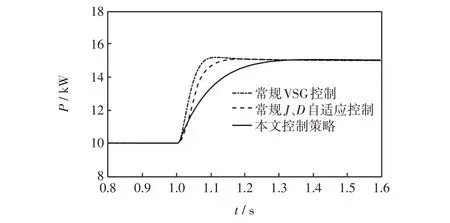
图11 不同控制策略下系统有功功率变化Fig.11 Changes in active power of system under different control strategies
综上所述,通过分析不同控制策略下系统输出角频率偏移及有功功率的变化情况可看出,本文所提出的基于改进粒子群算法的阻尼及惯量自适应控制策略相较于恒定参数控制策略及常规J、D自适应控制策略在输出响应超调量及调节时间等系统动态性能指标上均有较大提升,可验证本文所提出的控制策略的可行性及优越性。
5 结 论
针对虚拟同步发电机控制策略存在暂态调节时间长、动态性能较差等问题,本文在现有VSG 控制策略基础上,提出一种基于改进粒子群算法的阻尼惯量自适应控制策略,主要结论如下。
(1)改进惯性权重并引入耦合中心游移初始化和边界邻域更新策略对粒子群算法进行优化;设计以系统输出角频率偏移最小为目标的适应度函数,对VSG 阻尼惯量自适应控制策略的初始参数进行选取。
(2)分析系统振荡时的功角和阻尼惯量变化情况及对系统稳定性的影响,在系统暂态功角特性基础上对传统VSG参数控制理论进行改进,确定阻尼惯量自适应控制策略,并设计相应的自适应函数。
通过固定参数控制策略、自适应VSG控制策略及本文所提出的控制策略进行对比,结果表明,本文所提出阻尼惯量参数自适应控制策略可使系统在受到频率扰动时能更好抑制波动,并提升系统的稳定性。综上,基于改进粒子群算法的阻尼惯量自适应控制策略能够有效抑制电网低频振荡,提升系统稳定性,但随着电网趋于复杂化,振荡环境也逐渐多变,后续将针对复杂场景下控制策略的泛化性问题展开研究。

