基于分数阶滑模的混合微电网接口变换器电压稳定控制

王 浩，聂晶莹，李 斌，康博阳，张国澎

（1.河南理工大学电气工程与自动化学院，焦作 454003；2.河南省智能装备直驱技术与控制国际联合实验室，焦作 454003）

目前，构建以新能源为主体的新型电力系统正逐渐成为能源电力行业践行“双碳”目标的根本途径。随着可再生能源高比例渗透和配电网有源化程度提高，通过构建能够高效消纳分布式发电与储能，以及有机整合各类负荷的微电网系统，已成为解决配网侧新能源消纳与可靠并网的主要方式[1-2]。

不同于交流或直流等单一类型微电网，交直流混合微电网通过互联接口变换器IIC（interlinking interface converter）连接交流子网与直流子网，由此建立的交流与直流母线可以灵活接入各种类型分布式发电及交直流负荷，同时子网间还可以通过IIC实现功率传输和相互支撑[3-4]。

IIC是实现交、直流子网功率双向传输与分配的关键设备，能量的频繁流动会使直流母线电压发生波动[5-6]。在并网运行的交直流混合微电网中，为了抑制交直流混合微电网中直流母线的电压波动，提高系统运行稳定性，国内外学者围绕IIC对直流侧母线电压稳定开展深入研究。文献[7]提出一种基于IIC的虚拟同步发电机控制策略解决传统下垂控制功率分配精度低的问题，但负荷投切瞬间直流侧母线电压波动较大；文献[8-9]根据直流母线电压判断系统运行状态，提出一种基于IIC的改进下垂控制自主切换工作模式，但母线电压仍在一定范围内波动。文献[10]提出一种系统功率按比例分配的双向AC/DC换流器外环功率控制策略，但双向接口变换器输出电流变化滞后于扰动电流，使直流侧母线电压产生较大波动；文献[11-12]利用直流有源电力滤波器DC-APF（DC active power filter）输入端电容抑制直流母线电压纹波，但需同时考虑多个DC-APF 的并联均流控制；文献[13]提出一种针对电压骤降时变换器交流侧负序电流控制的方法，抑制直流母线电压的波动，但控制系统的电流参考值计算难度较大；文献[14-15]采用改进型空间矢量调制SVPWM（space vector pulse width modulation）的比例-积分双闭环控制策略减小直流侧电压波动，但适用电压等级不高。上述传统PI控制方法虽改善了电压稳态性能，但存在电流内环难以获得理想电压动态响应及电压外环抗干扰性差等问题，实际应用仍具有较大局限性。

相关学者和专家采用现代控制方法对电力电子变换器及其级联系统开展深入研究，其中，尤以滑模控制最具代表性，但针对并网型交直流混合微电网，相关文献很少涉及IIC 的非线性控制策略的研究。文献[16]提出将滑模控制应用于三相PWM整流器中，对直流母线输出电压进行控制；文献[17-19]为增强系统鲁棒性，提出一种应用于PWM 整流器的混合非线性控制方法，但该研究仅局限于滑模控制在PWM整流器中的应用；文献[20]在DC/DC双向变流器前馈控制环中加入非线性扰动观测器，但未涉及交直流混合微电网应用场景；文献[21]提出一种基于固定频率脉宽调制的滑模电流控制策略，较好地抑制了由外部扰动引起的直流母线电压波动，同时提升了动态响应速度。然而，上述研究仍存在以下问题：①对于整流、逆变工作模式自主切换并无较多涉及；②适用于交直流混合微电网背景下的研究较少；③多从混合非线性角度出发设计单环滑模控制器，缺少从双闭环出发设计电压变结构及电流分数阶滑模控制器的深入探讨。

综上所述，为实现并网型交直流混合微电网直流侧母线电压稳定及满足动态响应速度快的要求，本文提出一种基于分数阶滑模控制的交直流混合微电网IIC电压稳定控制策略。首先，根据IIC拓扑结构建立其两相同步旋转坐标系数学模型；然后，根据数学模型推导可控标准型状态空间表达式；接着，针对控制目标设计滑模面，建立电压变结构和电流分数阶滑模控制器；最后，通过MATLAB/Simulink 仿真和RT- LAB半实物平台验证了该控制策略的有效性，并与传统PI控制及传统单环滑模控制进行了对比。

1 混合微电网结构与数学模型

1.1 交直流混合微电网结构

交直流混合微电网一般由交流子网、直流子网及互联接口变换器构成，其基本拓扑结构如图1所示。并网运行时通过公共接入点PCC（point of common coupling）接入电网，IIC作为连接交直流母线的桥梁，控制交直流子网之间的能量流动，对维持交直流混合微电网的稳定运行起着决定性作用。

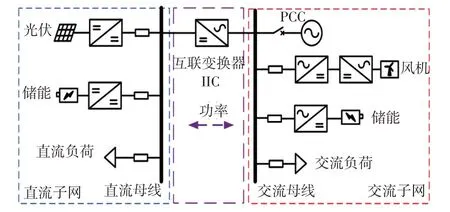
图1 交直流混合微电网示意Fig.1 Schematic of AC/DC hybrid microgrid

1.2 互联接口变换器结构及数学模型

交流子网与直流子网通过互联接口变换器连接，互联接口变换器拓扑结构如图2所示，由图2的IIC拓扑结构建立数学模型。

图2 互联接口变换器拓扑结构Fig.2 Topological structure of interlinking interface converter

图2中，ea、eb，和ec为交流微电网等效电源；L为输入电感；R为等效阻抗；C为直流侧电容；Udc为直流侧电压；RL为负载；idc为直流侧电流；Va、Vb、Vc、、和为开关函数，其中导通为1，关断为0；ia、ib和ic为三相电流。

对交流侧建立三相回路电压方程，直流侧建立电流方程，其可分别表示为

式中，vNO为N、O两点间的电压。

将式（1）、（2）由三相静止坐标系变为两相同步旋转坐标系，其矩阵形式可表示为

式中：id、iq为三相电流在d、q坐标系下的两相分量；ed、eq为三相电压在d、q坐标系下的两相分量；Vd、Vq为开关函数的d、q两相分量。

2 互联接口变换器滑模控制

滑模变结构控制算法以其对于非线性系统控制的优越性，成为电力电子控制领域的一个重要研究方向。为使并网运行的交直流混合微电网直流侧母线电压在能量频繁流动时减小电压波动，同时提高系统的响应速度，本文设计了基于SVPWM 的IIC混合微电网直流母线电压控制策略。

电压外环采用滑模变结构控制，充分利用其对系统参数变化及负载扰动的强鲁棒性。利用同步旋转坐标系中电流分数阶滑模控制器输出的空间电压矢量指令，提高系统响应速度；再经过SVPWM使IIC 的空间电压矢量跟踪给定值，以期达到电流控制的目的。通过分析互联接口变换器d、q坐标系下的式（3）可知，该系统有2个变量需要进行控制，因此设计2 个控制参数Sd、Sq，其中，Sd控制直流侧电压Udc，Sq控制无功电流iq。

由式（3）可推出IIC 可控标准型状态空间表达式为

2.1 电压外环变结构滑模控制

电压外环的控制目标是使被控变量跟踪参考值，选取参考值和实际值的误差作为状态变量，则滑模面设计可表示为

式中：Udcref为电压给定值；β为电压环滑模控制参数。

将式（4）代入式（5）可得

由三相平衡系统单位功率因数稳态运行可得

式中，Erms为输入交流电压相电压有效值。

将式（7）～（9）代入式（6）中，可得外环电压调节方程为

式中，id_ref为d轴电流内环参考值。

由式（10）可得滑模电压变结构电压外环控制框图如图3所示。在该控制系统中，为了降低系统误差，提高追踪精度使系统不受内部参数变化的影响，一般选取电压给定值Udcref=650 V。

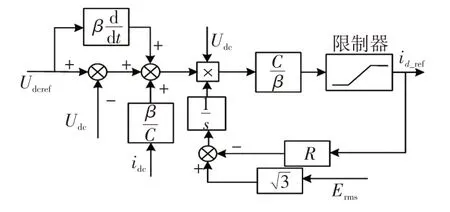
图3 电压变结构滑模控制框图Fig.3 Block diagram of voltage variable structure sliding mode control

由图3 可以看出，当IIC 采用双闭环控制系统时，电压外环的输出就是电流内环的电流参考值，据此完成内环电流的跟踪控制。

2.2 电流内环分数阶滑模控制

电流内环分数阶滑模控制的目标是确保网侧交流电流能快速跟踪指令电流值，即选取参考值和实际值的误差为状态变量，据此可设计滑动面为

式中：Si_d控制d轴电流；Si_q控制q轴电流；id_ref为控制系统跟踪的d轴参考电流；iq_ref为控制系统跟踪的q轴参考电流。

为使系统能够在滑模面上做滑模运动，设计一个滑动向量δ，其可表示为

选择合适的趋近律为有效抑制抖振，确保系统状态变量能在有限时间内到达滑模面，本文将分数阶微积分算子引入滑模趋近律设计中，构成分数阶指数趋近律，分数阶微积分积累了函数在一定范围内的全局特性，对历史信息具有一定的记忆性，可以使被控系统以较小的抖振快速收敛到给定滑模面，从而在一定程度上提高系统的控制效率。对滑动向量δ求导可得

式中：Dα为分数阶微积分算子，α为分数阶阶次，0 ≤α< 1，α= 0 时式（14）为整数阶指数趋近律；εd、εq、kd和kq均为趋近律参数，且大于0。

分数阶趋近律相对于整数阶趋近律多了微分阶次α这个可调参数，具有更好的调节灵活性，更有可能使被控系统以较小的抖振快速收敛到给定的滑模面，从而提高系统的综合控制品质。

为实现电流内环解耦控制，将耦合电流从控制律中移除，可得

式中，ud、uq分别为d、q轴电流内环输出值

将式（15）代入式（3）、（11）和式（12），化简后可得

为保证系统的稳定性，基于式（14）构建李雅普诺夫函数为

将式（14）代入李雅普诺夫函数式（17）并求导可得

由于ε>0、k>0，则式（18）是负定的，因此系统会在S=0处趋近于稳定。

以d轴电流控制为例，由式（15）给出d轴电流滑模控制框图如图4所示。

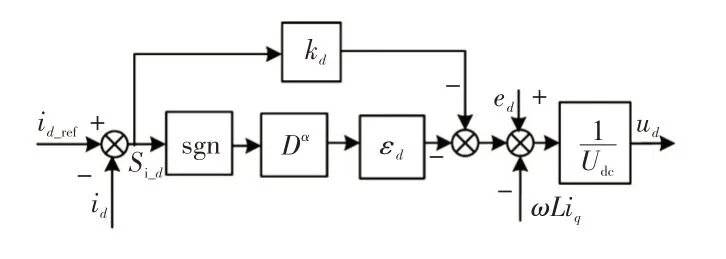
图4 d 轴电流分数阶滑模控制框图Fig.4 Block diagram of d-axis current fractional-order sliding mode control

同理可得q轴上的电流控制框图。值得注意的是，为获得单位功率因数的控制效果，一般iq-ref=0。

综上所述，d、q坐标系下的电流内环输出值ud、uq变换为α、β坐标系下的uα、uβ后，经过空间矢量调制的电压环变结构、电流环分数阶滑模控制器总体控制方案如图5所示。

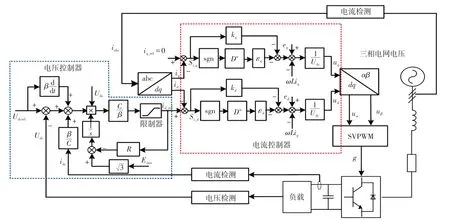
图5 互联接口变换器总控制框图Fig.5 Overall control block diagram of interlinking interface converter

3 仿真分析及实验

3.1 仿真分析

为验证所提策略的正确性和有效性，基于MATLAB/Simulink 平台，搭建图5 中的交直流微电网IIC 仿真模型及本文所提控制策略。其中，交流侧直流母线电压并网连接，额定频率为50 Hz、额定电压380 V；交流侧输入电感L=0.004 H、等效电阻R=0.1 Ω；直流侧滤波电容C=3 300 μF、阻性负载40 Ω；系统控制模块由电压控制器、电流控制器及空间矢量模块构成。为验证本文所提控制策略的优越性，将其与单环滑模控制及传统PI控制器进行仿真对比，所提控制系统及电流比例积分参数Kip、Kii，电压比例积分参数Kvp、Kvi设置如表1所示。

表1 控制系统参数Tab.1 Parameters of control system

由式（6）可以看出，β是设定的输出电压Udc的一阶导数的相关常数，因此该控制策略的动态响应性能受参数β的影响。分别对不同β的取值进行仿真，其结果如图6所示。由图6可以看出，当β增大时，响应速度也会有所加快，但其值不能过大，否则会对建模时忽略的功率器件开通、延时等产生较大影响，改变动态响应结果。

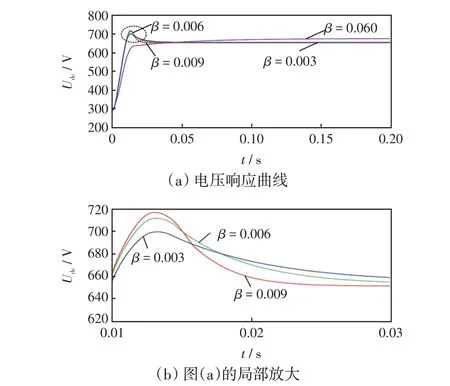
图6 不同参数下直流母线电压动态响应曲线Fig.6 Dynamic response curves of DC bus voltage under different parameters

当IIC 工作在整流状态时，由系统开始运行到稳定运行，不同控制策略下的响应结果如图7所示。

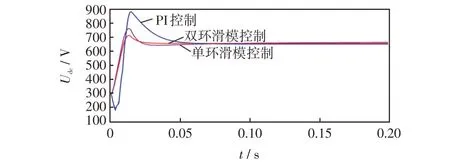
图7 不同控制策略直流母线电压动态响应Fig.7 Dynamic response of DC bus voltage under different control strategies

由图7可以看出，分数阶滑模控制直流母线电压达到给定值的响应时间在0.025 s左右，而传统单环滑模控制及PI 控制策略下的响应时间将近0.05 s，分数阶滑模控制的动态性能比其他两种控制提升近50%；分数阶滑模控制下的超调抑制效果也明显优越其他两种控制。证明电压变结构滑模能够有效抑制电压追踪的超调量，而电流分数阶滑模则能够提高系统的响应速度。

在稳定运行0.25 s后，负载发生突变，图8为负载突变时直流母线电压波形。由图8可以看出，负载突变后分数阶滑模控制的调节时间比PI 控制更短，调节过程中的电压纹波也明显比PI 控制的更小，验证了滑模控制器的抗干扰能力强。

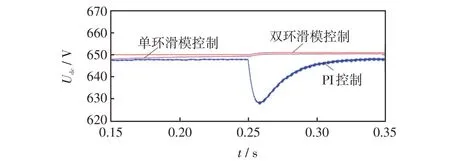
图8 不同控制策略负载突变直流母线电压波形Fig.8 Waveforms of DC bus voltage with load mutation under different control strategies

在并网连接时，交流侧母线电压的额定值为电网额定电压380 V，根据微电网中负载接入情况分析可得交流侧电流输出波形如图9所示。由图9可以看出，三相交流端输出电流过渡到稳定运行状态后，在0.25 s 发生负载突变后能够迅速恢复平稳状态，且三相电流波形对称度良好，能够达到国家标准正常运行的要求。

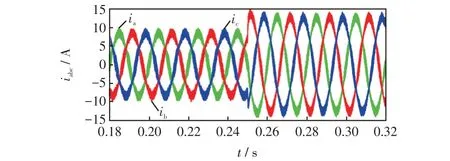
图9 三相交流输出电流波形Fig.9 Waveform of three-phase AC input current

3种控制策略下交流端A相电压电流波形如图10 所示。由如图10 可以看出，分数阶滑模和传统单环滑模控制下电压电流基本同相位，而PI控制下的电压电流相位存在较大偏差，因此，滑模控制下的变换器具有更高的功率因数，更接近1；图10（c）中的电流波形相较于图10（a）、（b）具有明显的谐波，说明滑模控制下能够获得更好的电能质量；两种滑模控制下的交流A相输出无明显差别，从侧面说明了分数阶滑模控制不仅在电压稳定性能方面有所提升，且在电流谐波抑制上也不输于传统滑模控制。

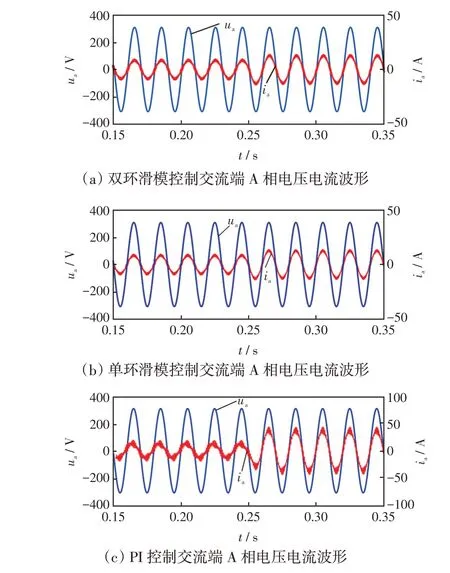
图10 不同控制策略交流端A 相电压电流波形Fig.10 Waveforms of phase-A voltage and current at AC terminals under different control strategies

根据直流侧母线电压的需求，变换器能够自主切换整流逆变模式。两种模式切换的功率流动如图11 所示，切换过程中电压电流波形如图12 所示。由图12 可以看出，在该控制策略下两种模式间能够平滑切换，稳定过渡到稳态运行。

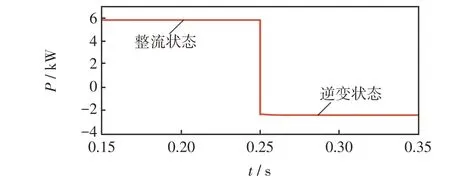
图11 自主切换功率流向Fig.11 Power flow direction during autonomous switching

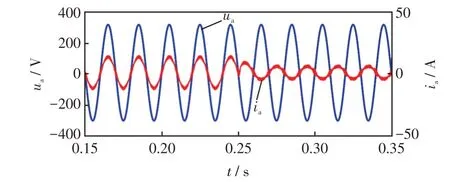
图12 自主切换电压电流波形Fig.12 Waveforms of voltage and current during autonomous switching

图13 为IIC 工作在逆变状态时，不同控制策略下A 相并网电压及电流输出的波形图。由图13 可以看出，两种滑模控制在逆变状态下的A相输出并无明显区别，但二者的电流输出波形都比传统控制下的逆变电流具有更好的正弦度，在负载扰动时，能相对更平滑地过渡至稳定状态，表明分数阶滑模在逆变状态下同样具有适用性。

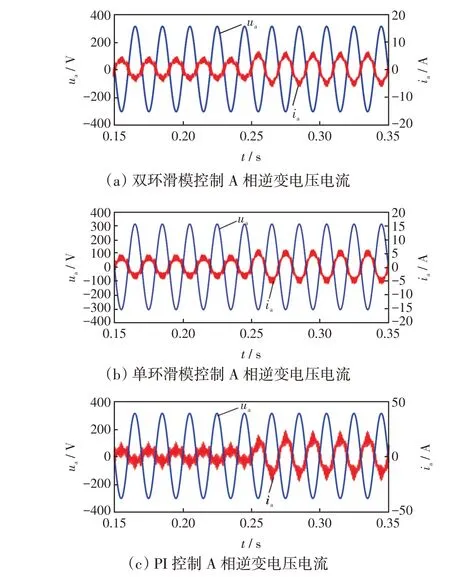
图13 逆变状态交流侧A 相电压电流Fig.13 Phase-A voltage and current on AC side in inverter state

通过对图13 中的电流波形进行谐波分析，可以得出3 种不同控制策略下的低次谐波畸变率如表2 所示。由表2 可以看出，本文所提控制策略谐波含量明显少于PI控制，却比单环滑模控制的谐波含量高，但二者差别不大，波形畸变率基本相等，相较传统控制有明显改善。因此，综合电压追踪及响应速率，本文所提控制更具优越性。

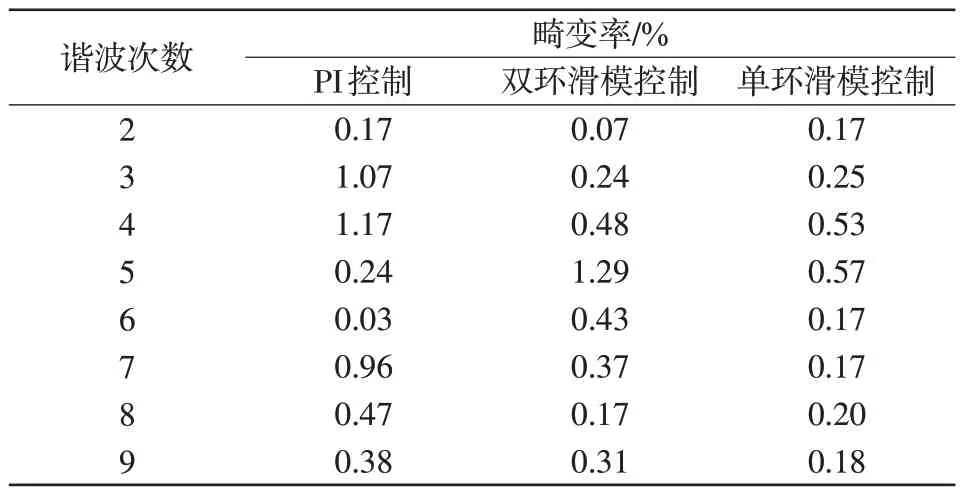
表2 电流谐波畸变率Tab.2 Current harmonic distortion rate

逆变状态下的直流母线电压如图14（a）、（b）所示。由图14（a）、（b）可以得出，3种控制策略下的直流母线电压根据给定电压追踪值稳定母线电压的响应时间有所不同，本文所提控制策略相较传统PI控制及单环滑模控制的动态性能和追踪精度有所提升。负载突变后母线线电压如图14（c）所示。由图14（c）可以看出，负载突变后本文所提控制策略的瞬态响应效果也更好，超调现象得到有效抑制，负载突变的切换更加平滑。

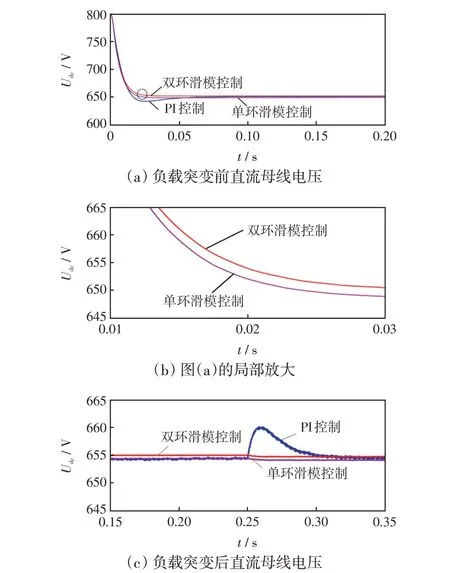
图14 不同控制策略逆变状态直流母线电压Fig.14 DC bus voltage in inverter state under different control strategies

3.2 实验验证

为进一步证明本文所提控制策略的有效性，搭建基于RT-LAB 的交直流混合微电网实验平台，该平台主要由主电路、信号采集电路和控制电路3部分共同构成。由图2中的交直流混合微电网IIC 拓扑搭建硬件电路，软件控制电路则是通过建立MATLAB/Simulink与RT-LAB之间的联系，将图5中的控制模型编译自动生成代码并下载到RT-LAB处理器中；信号采集电路则是连接硬件电路和控制电路的桥梁，采集并传输电压、电流信号；实验平台如图15所示，实验参数设置见表3。实验对比了不同控制下的直流侧母线电压稳定效果及交流侧电压电流的波形畸变率。

表3 实验参数Tab.3 Experimental parameters

图15 RT-LAB 实验平台Fig.15 RT-LAB experimental platform

图16 给出了在滑模控制策略下IIC 根据直流侧母线电压需求由整流自主切换到逆变过程的实验结果。实验结果表明，切换过程过渡平滑且迅速。

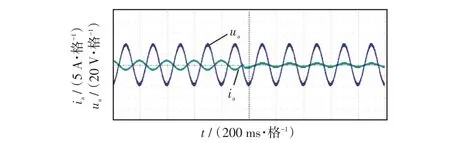
图16 自主切换实验结果Fig.16 Results of autonomous switching experiment

图17 给出了对比不同控制策略的直流母线电压波形。实验结果表明，本文所提控制策略在响应速度上具有明显优势，有效抑制了超调现象。

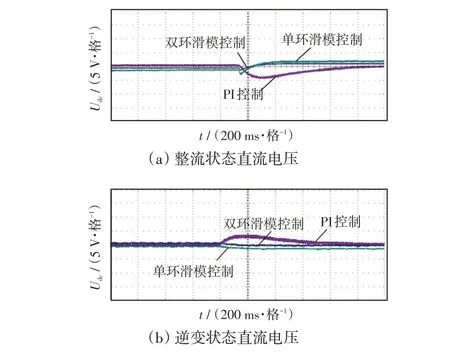
图17 直流电压实验结果Fig.17 Results of DC voltage experiment

两种工作模式下的交流电压电流实验波形如图18 所示。实验结果表明，分数阶滑模控制具有更优越的波形，电压电流相位基本相同（整流）或相反（逆变）。

综上所述，基于RT-LAB 的半实物实验验证了本文所提控制策略在IIC的两种工作模式间能迅速平滑切换，比传统控制的电压波动抑制效果更好；负载突变后能更迅速地恢复至稳定状态，具有更强的抗干扰能力；滑模控制下的交流侧逆变电流波形正弦度良好，谐波含量明显少于传统PI 控制，突出该控制策略的实用性及优越性。

4 结 论

本文提出一种分数阶滑模控制的交直流混合微电网互联接口变换器电压稳定控制策略，实现了交直流混合微电网直流侧电压稳定控制，提升了电压追踪动态响应性能。

（1）将分数阶滑模控制应用于交直流混合微电网的IIC中，在并网运行时，该控制策略能够对直流母线电压进行控制，实现整个系统的稳定运行。

（2）该控制策略能根据直流子网能量需求自主切换工作状态，完成整流/逆变的双向切换，响应速度相较于传统控制及单环滑模控制提升近50%，功率因数较高。

（3）当发生外部扰动时，负载的变化会引起直流母线电压的波动，本文所提的双闭环滑模控制能够较好抵御外部扰动，使母线电压迅速恢复追踪值并减小纹波电压，抑制瞬态响应超调现象，具有较好的鲁棒性。