多直流馈入受端电网的最大受电能力估计方法
李建华,王国腾,陆建宇,张怡静,黄 莹,徐 政
(1.国家电网有限公司华东分部,上海 200120;2.浙江大学电气工程学院,杭州 310027)
电源中心和负荷中心通常存在分布不均衡的问题,为了解决此问题,有学者提出利用基于电网换相换流器的特高压直流输电技术实现大容量远距离的电力资源转移[1-2]。随着特高压直流系统数量和容量的增大,受端电网逐渐演变成直流功率高渗透的多直流馈入受端电网[3]。和同步机的交流电压响应特性不同,电网换相换流器LCC(line commutated converter)不能为交流母线提供电压支撑。在交流母线电压跌落后,LCC甚至会增大吸收无功功率,进一步恶化系统电压稳定性[4-5]。电压调节不同于频率调节,其具有分布式特点。因此,对于某一负荷母线或换流母线而言,远端的同步机难以为其提供电压支撑。考虑到基于LCC 的高压直流HVDC(high voltage direct current)输电系统(即LCC-HVDC)的静态电压稳定约束,直流馈入功率可能无法达到预期目标,确定受端电网可接受的最大直流馈入功率是保障多直流馈入受端电网安全稳定运行的重要前提。
在静态电压稳定约束下估计多直流馈入受端电网的最大受电能力,其前提是找到一种可以准确评估多直流馈入受端电网静态电压稳定性的方法。目前,学者们大多采用电网强度的概念来衡量受端电网的静态电压稳定性,包括广义短路比[6]、综合短路比[7]及戴维南等效阻抗[8]等。这类评估方法也被广泛应用于电网的运行与规划中,例如文献[9]利用广义有效短路比建立了联合优化直流落点和机组出力分配的模型;文献[10]基于广义短路比与光伏接入容量间的灵敏度,提出了光伏多馈入系统的并网点容量优化方法;文献[11]研究了多馈入短路比与直流最大传输功率的关系;文献[12]将广义短路比应用于电网结构的规划当中。基于短路比和等效阻抗的方法通常需要将交流系统等值为带阻抗的电压源,而直流系统则采用详细模型,进而给出系统的静态电压稳定性。这类方法本质上是研究换流站母线的电压稳定性,并不能反映全局稳定性。考虑到直流系统与负荷之间的相互作用,多直流馈入受端电网负荷节点的静态电压稳定性也需要被重点关注。
目前,无功规划[13]、薄弱区域识别[14-15]和输电能力评估[16-18]是受端电网静态电压稳定性分析的重要方法。然而,现有方法忽略了受端电网存在最大可接受直流功率限制的问题。也就是说,当直流馈入功率超过一定阈值时,考虑静态电压稳定约束的最优潮流、机组组合模型可能都是无解的。因此,受电能力的估计是多直流馈入受端电网首先需要解决的问题。目前尚未有公开文献对静态电压稳定约束下多直流馈入受端电网的最大受电能力进行研究。
为解决这一问题,本文提出一种静态稳定约束下多直流馈入受端电网的最大受电能力估计方法,从而为电网运行提供参考,避免直流馈入功率占比过高带来的受端电网静态电压失稳问题。该估计方法由两部分组成:①考虑静态电压稳定约束的优化调度模型,利用奇异值理论刻画多直流馈入受端电网的静态电压稳定约束;②最大受电能力估计方法通过将优化调度模型分解成多个线性优化模型,便于调用商业求解器快速求解,并基于优化调度结果给出最大受电能力估计值。
1 系统模型
多直流馈入受端电网的拓扑结构示意如图1所示。同步发电机的开机方式决定了交流系统的强度,同时直流功率的变化也会改变直流系统和交流系统之间的强弱关系,进而影响系统的电压稳定性。
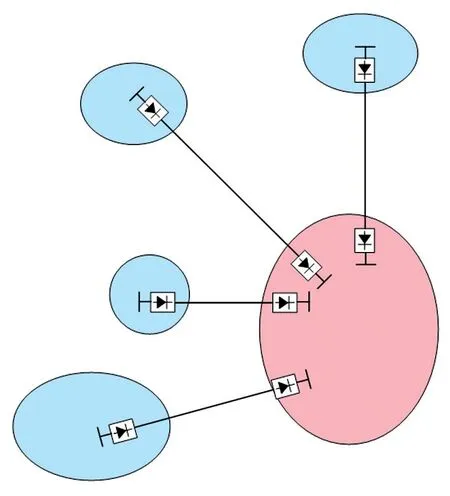
图1 多直流馈入受端电网示意Fig.1 Schematic of multi-infeed receiving-end power grid
交流系统中各个元件的模型可以参考文献[19],这里不再赘述。下面主要介绍本文采用的直流系统模型。常用的逆变侧LCC 的典型结构为12脉波换流器,如图2(a)所示。本文重点分析受端电网最大受电能力的估计,因此只考虑LCC作为逆变站的模型。在系统对称平衡运行条件下,LCC交流侧等效电路模型如图2(b)所示,其可以用代数方程组描述为
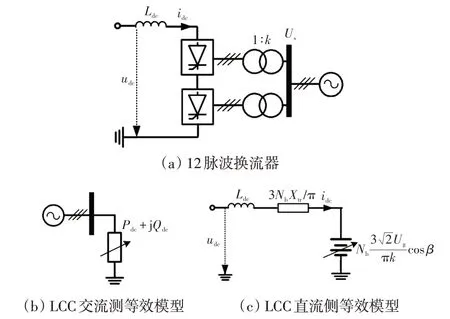
图2 逆变侧LCC 拓扑结构示意Fig.2 Schematic of LCC topological structure on inverter side
式中:Pdc、Qdc分别为LCC 向交流侧输出的有功功率和无功功率;idc为LCC 直流侧直流电流;μ为LCC 换相角;β为越前触发角;γ为关断越前角;Xtr为LCC 的漏抗;Us为交流母线电压;k为换流站的变比;Nb为六脉桥的数量;Ldc为平波电抗器的电感;udc为直流电压。
由图2(b)和式(1)~(4)可知,LCC 交流侧等效电路为代数方程描述的可变功率支路。而LCC 直流侧等效电路则为可变直流电压源串联阻抗形式,其等效电路模型如图2(c)所示,其可由一阶微分方程来描述,即
2 基于奇异值理论的电压稳定判据
2.1 电压稳定判据
一般来说,电力系统动态模型可以用微分代数方程组来描述,即
式中:x为状态变量组成的向量;y为代数变量组成的向量;f为微分方程组;g为代数方程组。对式(6)线性化可得
式中:Δx为向量x的变化量;Δy为向量y的变化量。
在任意时刻有
式中,Jgy和Jgx为系数矩阵。对于系数矩阵Jgy和Jgx,∂gi/∂yj为Jgy的第i行第j列元素,∂gi/∂xj为Jgx的第i行第j列元素,gi为第i个代数方程,xj和yj分别为第j个状态变量和代数变量。
传统雅可比矩阵是通过潮流方程线性化得到的,在潮流方程中LCC被处理成PQ节点,没有考虑到直流系统自身的电路特性。而本文中LCC不再是一个恒定的PQ节点,在雅可比矩阵中考虑了LCC自身特性的准稳态电路。因此,这里将矩阵Jgy称为扩展雅可比矩阵,扩展是指对直流准稳态模型进行扩展,即det(Jgy)=0,此时状态变量x一个很小的变化就会引起代数变量y出现很大的变化。在电力系统中,如果矩阵Jgy奇异,说明发电机转速或功角等状态变量的小扰动会引起节点电压大幅跌落,即电压失稳。相比于同步机转子运动,节点电压和注入电流的响应时间很短。在机电暂态时间尺度下,电网络暂态过程可以被近似忽略。将电力系统被等效成式(6)所示的模型,此时系统电压稳定性等价于矩阵Jgy的奇异性。
2.2 扩展雅可比矩阵的构造
扩展雅可比矩阵Jgy的构造仅和系统数学模型中的代数方程有关。系统中的代数变量也可以分为动态元件控制系统内部变量和电网络相关变量两类。其中,电网络相关变量一般指动态元件的注入功率和交流母线电压。电网络相关的代数方程由网络方程组成且不包含动态元件控制系统内部变量,仅与潮流方程和动态元件的注入功率相关。因此,扩展雅可比矩阵Jgy可以进一步分解为
式中:Jctr为动态元件控制系统代数方程关于控制系统内部变量的灵敏度矩阵;Jcn为动态元件控制系统代数方程关于电网络变量的灵敏度矩阵;Jnet为电网络相关代数变量关于电网络变量的灵敏度矩阵。
通过行消去可以将扩展雅可比矩阵Jgy改写为
根据上述分析,矩阵的行变换会使得同一个方程组中等号另一侧的变量也发生变化,从而导致变换后模型与原模型存在一定差异,故动态特性有所改变。但本文只关注系统的奇异性,矩阵变换前后不改变原矩阵的奇异性,因此这种变换对本文所讨论问题没有影响。这里将扩展雅可比矩阵Jgy的奇异性等同于矩阵Jctr或矩阵Jnet的奇异性。由于矩阵Jctr与动态元件的控制系统相关,故矩阵Jctr的奇异性代表控制系统内部是否稳定,而矩阵Jnet的奇异性代表电网络中节点电压是否面临崩溃风险。因此,本文仅关心矩阵Jnet的奇异性。
1)同步发电机注入功率方程
将同步发电机等价为一个带内阻抗的简单电源,内阻抗的电阻等于定子绕组的电阻Ra,内阻抗的电抗等于d轴暂态电抗,而电源电动势的大小E′在暂态过程中保持不变。同步发电机节点注入功率的表达式为
式中:Pg和Qg分别为发电机注入节点的有功功率和无功功率;δ为发电机功角;Ug和θg分别为发电机所连母线交流电压幅值和相位;Gg为暂态电动势;Gg和Bg分别为发电机导纳的实部和虚部,其表达式为
2)负荷注入功率方程
本文采用二次多项式模拟负荷的电压静态特性,即
式中:Pl和Ql分别为负荷注入节点的有功功率和无功功率;Pl0和Ql0分别为负荷注入节点的有功功率和无功功率初始值;aZ为恒阻抗负荷的占比;aI为恒电流负荷的占比;aP为恒功率负荷的占比;Ul为母线电压实际值;Ul0为母线电压初始值。
3)逆变侧LCC注入功率方程
逆变侧LCC向交流节点的注入功率表达式为
式中:Plcc为LCC 向交流节点的注入有功功率;Qlcc为LCC 向交流节点的注入无功功率;Qc为LCC 补偿电容输出无功功率。
4)节点功率方程
节点i的非线性方程为
式中:Ui为节点i电压幅值;Gi,j为节点导纳矩阵第i行第j列元素的实部;Bi,j为节点导纳矩阵第i行第j列元素的虚部;θi,j为节点i和节点j之间的相位差,θi,j=θi-θj;θi为节点i的相位。
将式(11)、式(13)和式(14)代入式(15)可以得到关于节点电压的非线性方程组为
式中:h为节点功率方程组成的非线性方程组;U为各个节点电压幅值组成的向量;θ为各个节点电压相位组成的向量。假设电力网络中共有n个节点,则方程组h中含有2n个方程,矩阵Jnet的维度为2n×2n,此时矩阵Jnet的表达式为
式中,hi为方程组h中第i个方程。
2.3 最小奇异值参数灵敏度
对矩阵Jnet进行奇异值分解可得
式中:V和Γ均为2n×2n的正交矩阵;τi为第i个奇异值;Λ为由奇异值组成的对角矩阵,奇异向量vi和zi分别为V和Γ中τi所对应的列向量。Jnet的行列式值为
因此,当任一奇异值接近0时,矩阵Jnet就接近奇异。令τmin为最小奇异值,则τmin越接近于0,系统越接近电压崩溃点。
矩阵Jnet中的变量可以分为两类:①式(6)中的可控状态变量x,例如发电机的功角δ、直流系统的直流电流Idc和负荷;②式(6)中的不可控代数变量y,例如节点电压幅值U和相位θ。通过调整可控状态变量x的大小,可以改变矩阵Jnet的最小奇异值。最小奇异值τmin随系统中任一变量xi的灵敏度为
式中:v和ψ分别为最小奇异值τmin对应的左、右奇异向量;xi为动态元件的状态变量。然而,任一状态变量xi的改变都会导致代数变量y随之发生改变,而代数变量y的变化又会进一步影响最小奇异值τmin。因此,需要对式(20)进行修正,得到最小奇异值随状态变量xi的变化灵敏度σx,i为
最小奇异值随电压幅值和相位的灵敏度为
节点电压幅值Uj或相位θj随状态变量xi的灵敏度可以通过隐函数求导方法得到,即
式中,yj为任一代数变量,这里是指节点电压幅值U或相位θ。
3 最大受电能力估计方法
3.1 调度优化模型
以多直流馈入受端电网为研究对象,合理安排系统开机方式,尽可能在保证多馈入受端电网电压稳定性的前提下降低系统运行成本。本文采用的机组启停成本及经济调度成本优化目标函数为
式中:T为运行时间尺度;ng为同步发电机的数量,zi,t表示机组i是否在运的二进制变量;cg,i为机组i运行的固定成本;oi,t表示机组i是否启动的二进制变量;co,i为机组i启动成本;ui,t表示机组i是否关机的二进制变量;cu,i为机组i关机成本;Pg,i,t为机组的输出功率;dg,i为燃料成本。
(1)同步发电机出力约束为
式中,Pgu,i、Pgl,i分别为同步发电机组i的出力上限和下限。
(2)同步发电机爬坡率约束为
式中,Ru,i、Rl,i分别为机组最大上坡率和最小下坡率。
(3)最小开、关时间限制分别为
式中:i=1,2,…,ng;t=1,2,…,T;Tup为机组的最小运行时间;Tdown为机组的最小关机时间。
(4)启动和关停约束分别为
(5)功率平衡约束为
式中:m为直流系统的数量;nl为负荷的数量;Pl,i,t为负荷i在时间t的大小;Pdc,i,t为直流系统i在t时刻的功率。
(6)电力系统所需的旋转备用容量约束为
式中,L%为针对系统负荷的旋转备用率。
(7)静态电压稳定约束为
式中:τth为最小奇异值的稳定裕度;τmin,t为t时刻系统最小奇异值;τmin,0为调整前最小奇异值的初始值。通过改变同步发电机的开机状态、同步发电机出力、直流功率和负荷模型参数,可以达到满足式(33)所示约束的目的。
3.2 最大受电能力估计
在优化模型中,利用灵敏度来衡量系统参数对最小奇异值的影响,将原有最小奇异值的计算转化成线性问题,然而这种线性化处理方式会给估计带来误差。估计结果距离初始点越远,误差越大,甚至会造成优化模型所得结果并非最优解的情况。为此,本文采用一种基于列和约束生成CCG(column and constraint generation)的迭代求解方法,利用迭代思想将系统模型分段线性化,以降低线性化带来的误差。这样优化模型可以写成矩阵形式为
式中:e为0-1 变量组成的向量;q为连续变量组成的向量;Dv、Dq、Av、Aq、Ev和Eq为参数矩阵;sv、sq、se为参数向量。
利用CCG 算法可以将问题分解为主问题和子问题两部分。主问题可以表示为
式中:ql为连续变量的限制向量,上标l为向量数量;ξ为辅助变量。
子问题可以表示为
式中,F为子问题函数。
在矩阵Eq、Ev和向量se中含有最小奇异值灵敏度,该灵敏度是通过线性化系统模型得到的,如果不加以修正,会使得优化结果误差较大。为此,根据主问题和子问题的优化结果更新矩阵Jnet中的系统参数,求解最小奇异值和最小奇异值关于优化变量的灵敏度。首先求解主问题和子问题,利用优化模型结果提供系统运行变量;然后通过奇异值及其灵敏度计算修正主问题和子问题中的矩阵,再次求解主问题和子问题,如此反复迭代,直至前后两次迭代计算结果相差在很小范围内,则迭代终止,得到最终优化结果。本文所提的受端电网的最大受电能力估计方法具体步骤如下。
步骤1选定直流落点及初始直流功率。一般来说,直流落点的选取受到地理位置、输电通道和投资成本等方面的限制。通过筛选得到所有备选直流落点后,可以假设这些直流落点均有直流系统馈入,然后进一步估计受端电网的最大受电能力。
步骤2求解优化调度模型。在给定直流功率下,若优化模型有解,则说明在该受电规模下可以找到一种运行方案满足静态电压稳定约束,这说明系统并未达到受电规模极限,此时进入步骤3;若优化模型无解,则说明在该受电规模下不存在运行方案能够达到静态电压稳定性的要求,这说明已经找到系统的最大受电能力,此时结束计算。
步骤3进一步提高多条直流系统的馈入功率,然后返回步骤2。
一般来说,直流系统的数目和接入位置是确定的,交流系统机组运行方式和直流系统的送电曲线是变化的。本文选择等比例提高多条直流系统功率来校核系统的最大受电能力。
4 算 例
本文所提出方法在一个修改的IEEE39节点系统中进行验证。仿真基于PSS/E,优化模型采用Gurobi求解。修改的IEEE39节点系统网架结构如图3所示,其中3个基于LCC 的单极直流系统分别接入节点9、节点14和节点17,主要参数如表1所示。
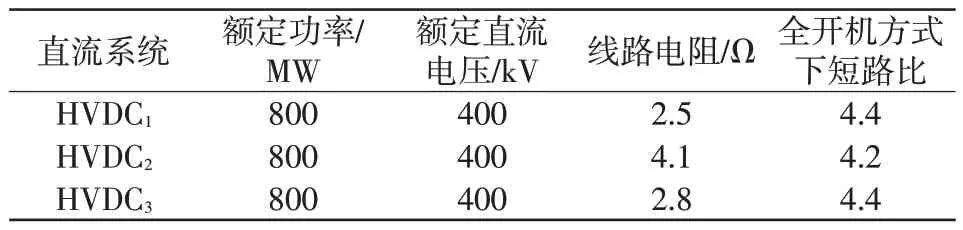
表1 3 个直流系统主要参数Tab.1 Main parameters of three DC systems
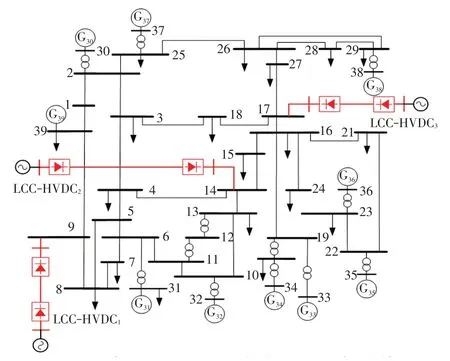
图3 修改的IEEE39 节点系统网架结构Fig.3 Grid structure of modified IEEE 39-bus system
4.1 考虑静态电压稳定约束对系统决策影响分析
为了分析静态电压稳定约束对系统调度决策的影响,在是否考虑静态电压稳定约束两种方案下进行分析。为保留裕度,将允许最小奇异值设定为0.05,可得到是否考虑静态电压稳定约束的优化结果分别如图4和图5所示。
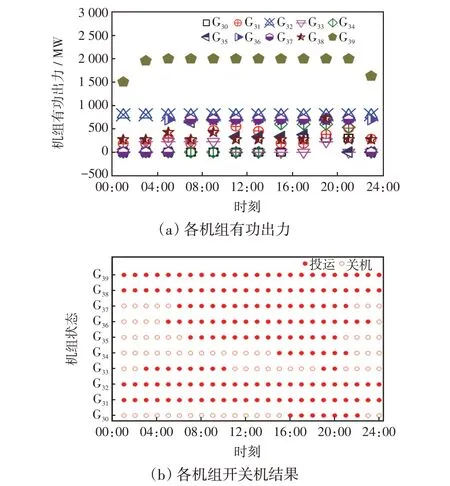
图4 不考虑静态电压稳定性约束下的调度结果Fig.4 Scheduling results without considering static voltage stability constraints
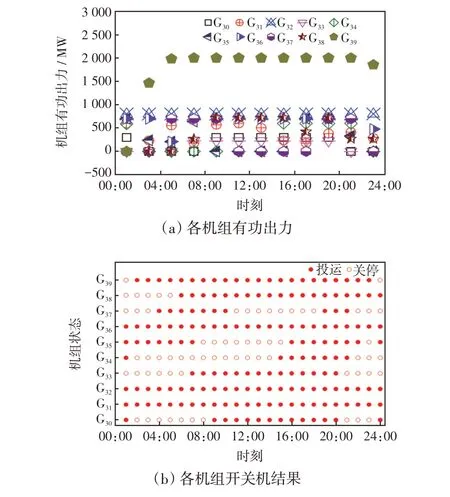
图5 考虑静态电压稳定性约束下的调度结果Fig.5 Scheduling results considering static voltage stability constraints
由图4 和图5 可知,两种方案在开机方式和机组出力上均有差别。在不考虑静态电压稳定约束时,系统中最多有6台机组不开机,对应时刻分别为01:00、02:00和24:00。在考虑静态电压稳定约束时,系统中不再出现6台机同时停机的工况,在01:00、02:00 和24:00 时刻的机组停机数量分别为4、5 和4。由于系统中机组停机数量越多,发电机对系统的电压支撑能力越弱,为达到经济最优目标将过多的机组停机会导致系统电压稳定裕度不足。因此,是否考虑静态电压稳定约束本质上是经济和稳定性两者之间的博弈。
两种方案下,系统的最小奇异值如图6 所示。可见,不考虑静态电压稳定约束的调度方案会导致系统在01:00、02:00和24:00时刻的最小奇异值小于0.05,稳定裕度较小,系统电压失稳风险增大。而考虑静态电压稳定约束的调度方案可以保证系统在全天24 h的最小奇异值均大于0.05。
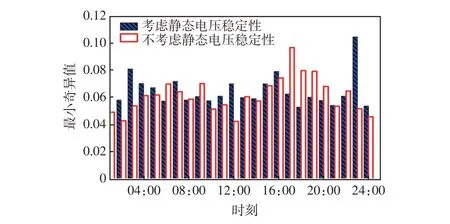
图6 不同调度方案下的最小奇异值Fig.6 Minimum singular values under different scheduling schemes
4.2 最大受电能力估计
在多馈入受端电网中,直流功率占比通常较高。然而,随着直流功率占比的增大,系统的静态电压稳定性将会变差。考虑发电机保持额定出力不变,为保证供需平衡,随着直流功率增加,应等比例增加各节点负荷。在全开机方式下得到系统最小奇异值随直流功率占比的变化曲线如图7所示。
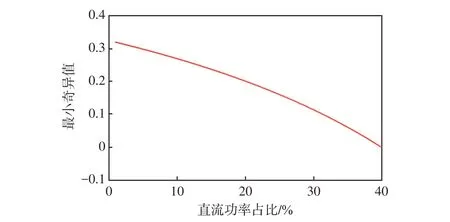
图7 系统最小奇异值随直流功率占比的变化Fig.7 Variation of minimum singular value of system with proportion of DC power
需要说明的是,在任意增加一个直流系统输送功率时,换流母线处的补偿电容也会随之增加,从而保证换流母线在稳态下的电压幅值保持在正常范围内。针对图3所示测试系统,当直流功率占比达到36%时,系统最小奇异值将小于0.05;当直流功率占比达到40%时,系统最小奇异值已经接近于0。可见,直流功率占比超过36%时,对于第3.1节所描述的优化模型已经无解,此时不论如何安排开机方式和系统潮流,都无法使得系统最小奇异值大于0.05。只能通过降直流功率、切负荷等稳控措施来增大系统最小奇异值,以满足系统对稳定性的要求。
在PSS/E 中调整系统参数,令直流功率占比达到40%,然后进行仿真计算。扰动设置为节点1 处发生100 Mvar 的无功阶跃,得到仿真结果如图8 所示。从图8(a)可以看出,无功扰动发生后,各母线电压不能稳定在一个稳态运行点,而是在某个范围内来回波动,结果表明系统不存在稳态运行点,发生奇异诱导分岔,数值计算结果已不具备可信性。图8(b)给出了扰动发生后各个发电机功角摇摆情况,结果表明系统并未发生功角失稳,也进一步说明了图8(a)所示的电压波动现象是电压失稳,而不是功角失稳。
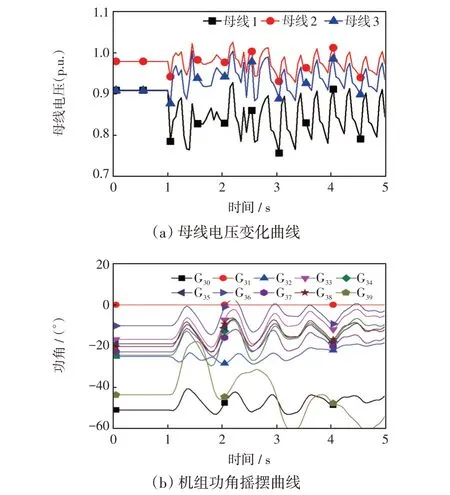
图8 无功负荷阶跃下仿真结果Fig.8 Simulation results under reactive load step
5 结 语
本文提出了一种静态电压稳定约束下多直流馈入受端电网的最大受电能力估计方法。首先,建立了考虑静态电压稳定约束的优化调度模型,以该模型是否有解来判断在当前受电规模下系统是否存在运行方式能够满足静态电压稳定性的需求,并基于该模型搜索系统的最大受电能力。然后,通过修改的IEEE39节点系统进行仿真分析,结果表明,所提模型的优化结果可以有效判断出满足静态电压稳定约束的运行方式。最后,利用所提模型研究受端电网的最大受电能力,结果表明,当直流功率占比过大时,不论采取何种开机方式,系统均无法稳定运行,此时直流功率即为受端电网的最大允许受电量。

