现货市场中实现保供目标的容量补偿定价方法
柴 玮,杜首行,陈 愚,王梓怡,舒 隽
(1.国能经济技术研究院有限责任公司科研发展部,北京 102211;2.华北电力大学电气与电子工程学院,北京 100096;3.国家能源投资集团有限责任公司战略规划部,北京 102211)
我国提出的“双碳”目标要求加快建设新型能源体系。但随着可再生能源装机量的增加及大规模并网,其极低的发电边际成本拉低了电力现货市场价格,导致传统的火电机组出现了缺失收入问题,部分火电机组无法在电力市场中回收固定成本,生存空间受到了挤压。火电机组效益降低严重影响了发电企业投资火电机组的意愿,甚至加速了一些已有火电机组的淘汰。但是,可再生能源作为间歇性能源,其发电能力由实时的天气情况决定,在一些极端无风无光且同时出现负荷高峰的情境下,电力系统就会出现发电容量不足的问题,影响电力负荷的可靠供应。因此,需要实施适合国内电力市场现状的容量成本回收机制,保证存量机组的合理装机水平,并引导发电企业投资。合理的容量补偿机制可以在一定程度上保证电力系统的可靠性,对于保持电力系统的长期供应均衡及推动可再生能源的健康可持续发展具有重要意义。
目前,在电力系统容量机制方面已有大量研究。文献[1]对如何以最低的合理成本提供可靠的电力进行了调查,指出应首先为供电可靠性设定一个合理的经济标准,并基于此提出了一种确保以最低成本提供可靠低碳电力的方法。而各国针对实现电力系统充裕性提出并实施了不同的容量机制。文献[2]详细梳理了国际上几种常见的电力现货市场配套容量机制,并结合我国现状,提出了采用容量补偿机制进行过渡。文献[3]在分析国外容量市场机制后,提出了一种适应我国的容量市场跨省区联合出清机制,并且完善了配套的容量需求曲线原则及机制设计。针对容量补偿机制的理论研究,除了文献[2]提出的协调容量电价的电源规划双层模型外,文献[4]建立了考虑容量补偿的火电机组双层决策模型,对不同可再生能源渗透率下容量补偿价格对火电企业决策及市场运行的影响进行了分析。文献[5]从中长期至现货全时间尺度上入手,解决了系统灵活性资源不足的问题,提出了一种激励火电灵活性改造的调峰容量补偿机制。
容量补偿机制相较于其他成本回收机制有较多优点。首先,由于其政策实施的便利性,对不同阶段的电力市场均有较好的适应性;其次,容量补偿电价和补偿容量都有明确规制方法,适合我国电力市场目前的改革阶段;最后,容量补偿机制直接根据容量贡献向市场内机组支付容量费用的方式,保证了发电企业可以稳定回收成本,传达了明确的投资信号,有利于保证电力系统的发电充裕度。目前,中国部分现货试点省份已经初步建立了容量成本回收机制。山东率先于2020 年提出了收取容量补偿费用,价格(含税)暂定为0.099 1¥/(kW∙h),并于2022 年提出了容量系数调整要求,采用负荷侧带分时系数的容量分摊机制。广东也提出了根据市场机组有效容量占市场机组总有效容量的比例来补偿各机组,实施容量补偿机制的主要目的是帮助发电机组成本回收,以保证未来年份的装机充裕性。文献[6]指出容量补偿机制具有诸多好处,从建设难度来看,容量补偿机制不同于容量市场和稀缺定价机制,是一种适用于新型电力系统初始阶段的过渡机制,不需要大量的技术和经验,实施的可行性较高;从机制建设风险来看,政府部门可以根据政策和市场具体情况来控制建设风险,有利于实现向新型电力系统的平稳过渡。
容量补偿价格的确定是容量补偿机制能否发挥正向作用的关键。文献[7]指出了目前容量补偿机制的潜在问题,其关键在于规制经济合理的容量补偿电价,若电价设定不合理,则会造成部分机组出现过补偿或欠补偿的问题,进一步扭曲现货市场电价,无法正确引导发电企业投资。文献[8]指出了容量补偿的关键是容量补偿对象确定、补偿费用核算、补偿费用分摊及补偿费用动态调节。对于容量补偿标准的确定,文献[9]对按中标容量和装机容量补偿进行了对比,得出按中标容量进行补偿能更好地体现各机组对发电容量充裕性的贡献。文献[10]给出了不同经济理论下的定价方法。文献[11]提出了根据市场中各机组的年化投建成本和运行盈利情况,并考虑其单位有效容量的成本回收缺额平均值,进而确定单位容量的成本补偿价格。文献[12]则定义月度单位容量补偿标准为单位容量年化固定成本和其他市场单位容量年收益相减后再乘以月补偿系数。文献[13-14]则采用边际成本法确定容量电价,并根据峰值负荷和电网阻塞情况调整充裕容量,最终确定补偿容量。
为保证补偿价格的合理性,在电力市场环境下对机组进行容量补偿必须考虑机组的现货收入,因此容量补偿定价过程中需要进行电力现货市场仿真。在电力市场仿真方面,文献[15]采用模拟市场规则、报价策略、投资策略的方法来研究发电容量长期充裕性的动态行为。文献[16]从系统动力学方面研究了市场环境与充裕性机制设计的关系,综合考虑机组的经济效益,设计了基于净现值评估的发电投资退役模型,构建了电力市场长期动态仿真模型,分析了几种不同容量机制对市场的影响。同时,容量机制需要配套充裕性评估机制来核定机组的有效容量,文献[17-18]论证了蒙特卡罗模拟方法在系统发电容量充裕性评估的适用性。文献[19]在蒙特卡罗法的基础下,实现了超大规模系统充裕性评估。文献[20]基于中心极限定理对蒙特卡罗法的抽样进行了改进,平衡计算精度和计算成本。文献[21]借助Stackelberg 博弈模型构建了发电容量充裕性评估的框架。文献[22]引入了缺电时间期望LOLE(loss of load expectation)作为可靠性指标,对比了不同充裕度机制对可靠性改善的情况。
目前,容量补偿电价的制定一般采用系统长期边际容量成本测算,仅考虑了一定时间内系统峰值负荷期间的边际机组,但此方法确定的容量补偿价格是否可以合理引导发电机组投资、退役,以保证未来电力系统可靠性,缺少相关的理论研究。同时,容量补偿费用并不等同于两部制电价,因为容量补偿机制是现货市场的补充,用于解决机组无法在现货市场中回收固定成本的问题,容量补偿电价设定过高会造成用户购电成本升高,反之,会造成长期发电充裕度不足。由于现有容量补偿价格的制定并没有综合考虑火电机组在现货、容量等方面的综合利润。因此,本文综合考虑火电机组的现货利润和容量收入,以及容量补偿价格对未来电力系统可靠性的影响,提出一种实现电力系统保供要求并计及发电企业电力现货市场经济效益的容量补偿定价方法。
1 电力市场容量补偿机制
1.1 容量补偿机制综述
国际上采用的容量成本回收机制主要有稀缺定价机制、容量市场机制、战略备用机制和容量补偿机制。其中,稀缺定价机制主要应用在美国ERCOT 电力市场和澳大利亚NEM 电力市场,这种机制的特点在于只存在单一的电力现货市场,可以在促进机组成本回收的同时节省电力用户的开支,并且对现货市场的行政干预最小;容量市场机制主要应用在美国PJM、NYISO 电力市场及英国电力市场,其特点在于由系统运营机构设定系统容量需求曲线,并通过集中式拍卖机制获得满足需求的容量水平和电源结构;战略备用机制主要应用在欧洲国家,其特点是系统运营机构拥有部分系统边际冗余容量,并在供需紧张时进行调用;容量补偿机制主要应用在秘鲁、智利等南美洲国家,这种机制建立在非市场环境下,由监管机构事先确定参数滚动调整容量补偿电价,并根据供需核算补偿容量的一种机组成本回收机制。针对发电侧通常会制定统一容量补偿电价,根据不同类型机组有效容量及系统峰值负荷确定各个机组的补偿容量,然后按照容量电价和机组补偿容量支付机组容量费用。
各国的容量补偿机制均存在一定的政策差异,并且有些国家会同时采用多种容量机制,例如意大利、西班牙和波兰还同时存在战略备用机制[23]。本文主要以智利的容量补偿机制为参考[24]。
智利的中央电力系统SIC(central interconnection system)为智利约93%的人口提供电力服务,2008年其发电来源中水电占比55.1%、天然气占比27.3%、煤炭占比9.7%、柴油占比7.4%、其他类型机组占比0.4%。在典型年水力发电提供约58.0%的总电量,然而在干旱年份水力发电量仅占SIC 总发电量的27.0%。因此,为了提高电力系统对极端天气的应对能力,智利电力市场在批发和远期合约市场外建立了集中容量市场,但其仅确定电能量价格,发电机组仍然按照容量补偿机制规制的容量补偿价格获得容量收入,以此来保障电力系统的充裕度维持在合理区间。
1.2 容量补偿机制主要环节
容量补偿机制主要由政府监管机构及调度机构制定运作,其关键在于容量电价制定和补偿容量核定。
容量补偿电价一般基于长期边际容量成本制定。长期边际容量成本是指在未来一定时间内电力系统增加单位发电容量所需的成本。市场环境下,容量电价由一定时间内系统峰值负荷期间运行的边际机组的投资成本折算得到的等额年金确定,其计算公式[14]为
式中:r为边际机组的单位容量电价;c为边际机组的单位容量建设投资成本;γ为折现率;n为边际机组的投资回收周期。
补偿容量核定包括初始容量核定、充裕容量核定及补偿容量核定。在初始容量核定时,不同类型发电机组分别核定,主要基于机组在历史时间内实际的发电功率进行测算;充裕容量核定主要考虑机组的厂用电率、年度检修计划、强迫停运率及平均修复时间等对机组可用性影响因素,对各个机组的初始容量进行下调;补偿容量核定是根据系统峰值负荷和线路阻塞情况对机组的充裕容量进行调整。
2 基于可靠性标准和内部收益率的容量补偿价格调整模型
2.1 基于内部收益率评估的机组决策模型
2.1.1 发电机组在现货市场和容量补偿的收入计算
本文采用基于安全约束机组组合和安全约束经济调度的电力现货市场长周期仿真模型,以发电成本最低为优化目标,输入参数为各类型机组的运行参数、输电安全约束、负荷时序需求等,约束条件包括供需功率平衡、火电机组的出力上下限、爬/滑坡率等。采用各类型机组的边际成本作为发电报价数据。长周期仿真的输出数据为全年8 760 h 所有机组节点边际电价和发电出力,进而通过统计计算所有机组当年的现货市场收入、成本及净利润。
本文采用的容量收入基于容量补偿机制进行计算,初始的容量补偿电价采用基于长期边际容量成本原理计算,即由负荷峰值期间运行的边际机组的单位投资成本核算等额年金,机组的容量收入由容量补偿价格和机组补偿容量确定。
2.1.2 内部收益率评估
由容量补偿机制规制的电价可以显著影响发电机组的投资和退役,进而影响未来年份电力系统的装机容量和装机结构。因此,本文构建了一种基于内部收益率IRR(internal rate of return)评估的发电机组决策模型。IRR 是效率型经济效果评价指标,目前多数发电企业在进行投资决策时采用IRR作为评价指标,反映项目为其所占用资金所能提供的盈利率,即净现值为0时的折现率。通常可以采用插值法求解IRR的近似值,净现值的计算公式为
式中:NPV(γ)为折现率为γ时的净现值;SMt为机组在第t年的现货市场净利润;CMt为机组在第t年的容量收入;CO0为机组在第0 年的建设成本;nc为机组的成本回收年限。
采用插值法求解IRR近似值的计算公式为
式中:IRR 为内部收益率;NPV(γa)和NPV(γb)分别为折现率为γa和γb时的净现值;σ为使用插值法计算IRR的精度参数。
由于本文重点研究容量补偿价格对机组决策的影响,因此在进行现货收入计算时,为了简化计算及体现发电商在进行决策时的有限理性原则,仅精确计算当前年份(第y年)的现货收入SMy,成本回收期内其他年份的现货收入则在此基础上进行合理预测,即
式中:SMy为精确计算得到的当前年份的现货收入;α为现货利润变动指标,受未来年份的机组燃料预测价格、负荷增长预测指标等因素影响。
传统火电机组属于资本密集程度较高的产业,因此发电企业在进行投资决策时需要综合考虑市场环境、技术选择、投资时机等因素,而IRR指标可以反映投资回报的内在性质,并且考虑了投资项目生命周期内所有的现金流量,因此能够比较全面地反映投资项目的经济效益。本文构建了基于IRR评估的机组投资/退役决策模型,该模型中新建机组决策需要保证同类型机组的IRR 高于基准折现率,即若某类型机组的IRR 高于设定的基准折现率,则发电企业会决策投资一台同类型机组,并可以在未来目标年份投产运行,作为目标年份可用的发电容量。而传统火电机组作为重资产投资,现有机组的退役决策并不能按照基准折现率进行评估。因此现有机组退役设定为某机组全生命周期的IRR小于设定的退役决策参考折现率时,在次年启动退役计划,且在目标年份无法提供可用容量,具体投资/退役模型策略可表示为
式中:IRRi为机组i的IRR;θi为发电企业设定的机组i的基准折现率;θr为设定的退役决策参考折现率。
2.2 发电结构决策迭代收敛模型
不同容量补偿价格水平会显著影响发电企业的投资决策,即影响目标年份市场的装机容量和电源结构,进而影响目标年份电力系统的可靠性,因此本文采用迭代收敛法来确定不同容量补偿价格水平下目标年份的装机结构。首先在给定容量补偿价格情况下,计算所有机组的IRR 指标,并根据指标结果进行单次投资/淘汰决策,若发生已有机组淘汰或机组新建,则使用新的装机结构重新进行电力现货市场长周期仿真,并进行IRR 评估;然后再次进行单次淘汰/投资决策,循环此过程直到不再发生投资/淘汰决策,此时装机结构就为该容量补偿价格水平下目标年份的装机结构。具体迭代流程如图1所示。
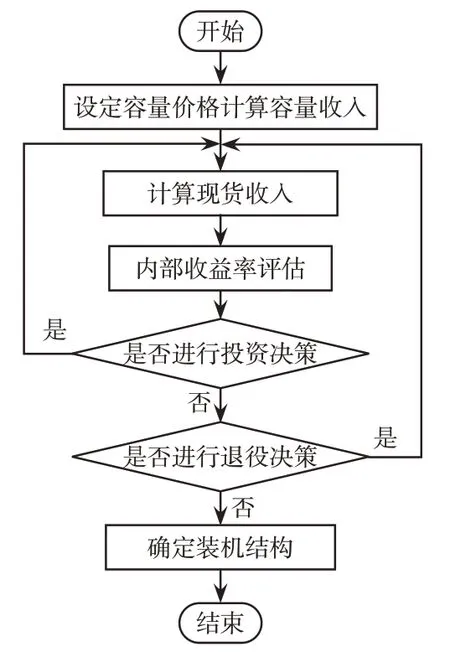
图1 发电机组决策流程Fig.1 Flow chart of decision-making for generators
2.3 基于可靠性的容量补偿价格调整模型
在确定目标年的装机结构后,采用基于序贯蒙特卡罗法的电力系统可靠性计算程序来计算目标年份的可靠性指标。电力系统的可靠性指标主要有缺电时间期望LOLE 和电量不足期望LOEE(loss of energy expectation),本文采用LOLE 作为可靠性评估指标。首先根据发电结构决策迭代收敛模型确定的装机结构和目标年份的电力系统边界数据及机组参数,计算当前发电结构下目标年份的LOLE;然后与可靠性标准进行比较,若低于可靠性标准,则说明目标年份装机容量不足,需要提高容量补偿价格,促进机组投资,反之则降低容量补偿价格,加速现有机组淘汰。
第j+1次调整的容量补偿价格可表示为
式中:LOLEj为第j次调整容量补偿价格后的目标年份的可靠性指标;LOLEO为可靠性标准,CPj为第j次调整的容量补偿价格;STj+1为第j+1 次调整容量补偿价格的步长。
为实现最佳容量补偿价格的快速准确求解,本文提出了以下价格调整方案,该方案由两阶段组成。具体流程如图2所示。
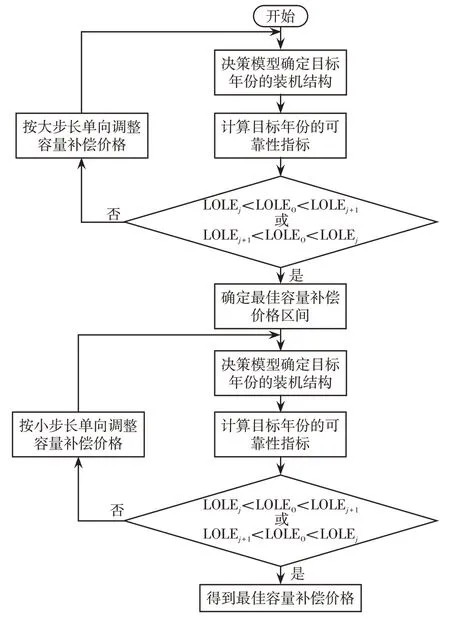
图2 容量补偿电价制定流程Fig.2 Flow chart of capacity compensation pricing
(1)确定最佳容量补偿价格区间。将基于长期边际容量成本计算得到的容量补偿价格作为基准参考,按照较大步长逐渐单向调整容量补偿价格,计算不同容量补偿价格下的目标年份可靠性指标LOLE。对比相邻容量补偿价格下LOLE 的变化情况,若相邻两次LOLE指标位于可靠性标准两侧,则这两次的容量补偿价格即为最佳容量补偿价格所在区间。
(2)确定容量补偿价格。确定最佳容量补偿价格区间后,按照小步长对区间内的容量补偿价格逐步增加,并分别计算不同容量补偿价格下的LOLE指标变化情况,若再次出现相邻两次迭代的LOLE指标位于可靠性标准两侧时,则选取两个指标中较小者所对应的容量补偿价格作为最终价格。
3 算例分析
本节构建算例对容量补偿价格的制定策略进行验证。本文算例中,发电侧有燃煤、燃气两类火电机组。考虑机组不同的装机容量,共有5种类型的火电机组,各类型机组的经济参数及可靠性参数如表1 所示,系统现有装机结构如图3 所示。可靠性参数来自《2021年全国电力可靠性年度报告》。
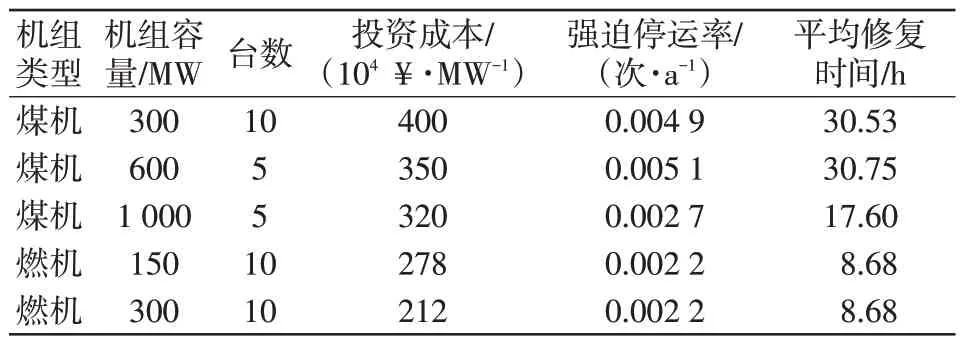
表1 机组运行参数Tab.1 Operation parameters of generators
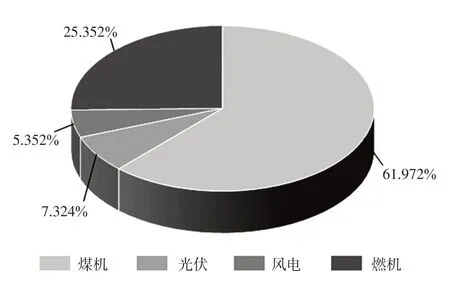
图3 各类型发电机组装机占比Fig.3 Proportion of installed capacity for different types of generators
本文算例起始年和目标年的负荷曲线、外来电、风电和光伏出力曲线均采用某地区2021 年的测量值和2025 年的预测值。假设所有机组的成本回收年限均为20 a,当前年份为2021 年,目标年份为2025年,现货利润变动指标α=1,目标年份的可靠性标准LOLEO=0.1 h/a。同时,为简化机组决策流程,本文算例设定所有火电机组的投产年份相同。首先对此地区2021 年电力现货市场进行长周期仿真,现货电价如图4所示。
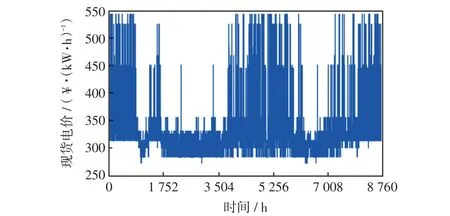
图4 全年时序电价曲线Fig.4 Curve of electricity price series in one year
1)确定初始的容量补偿价格
根据长期边际容量成本原理,选择现货市场中峰值负荷期间运行的边际机组为150 MW的燃气机组,设定折现率为6%,则初始的容量补偿价格计算式为
设定基准折现率为10%,退役决策参考折现率为0。由基于IRR评估的机组决策模型进行多轮机组决策,最终确定在容量补偿价格为24.2×104¥/(MW·a)的情况下,该地区2025 年的电力系统发电机组参数如表2所示。
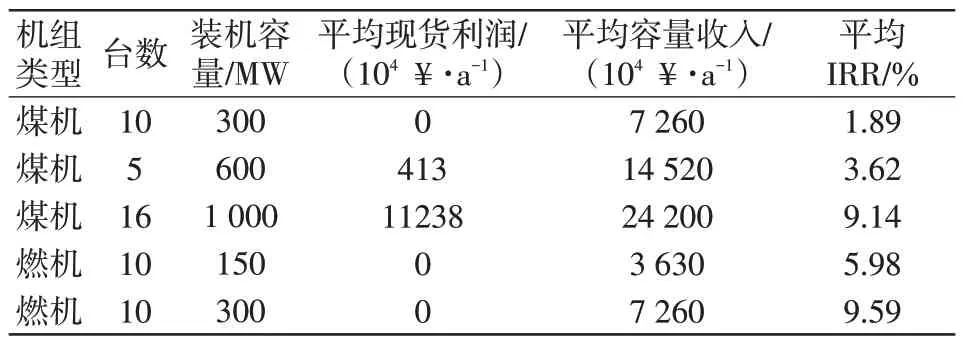
表2 发电机组类型和数量Tab.2 Types and quantities of generators
基于表2 所示发电机组参数计算得到的2025年可靠性指标LOLE 为0 h/a,即在容量补偿价格为24.2×104¥/(MW∙a)的情况下可满足可靠性标准。
2)调整容量补偿价格
首先按照大步长1×104¥/(MW∙a)单向调节容量补偿价格,确定容量补偿价格的最佳区间为160 000~170 000 ¥/(MW∙a);然后再按照小步长1 000 ¥/(MW∙a)单向调节容量补偿价格,计算得到当容量补偿价格为16.9×104¥/(MW∙a)时,目标年份的LOLE为0.129 h/a,大于设定的可靠性标准,而当容量补偿价格为17.0×104¥/(MW∙a)时,目标年份的LOLE为0.04 h/a,小于设定的可靠性标准。因此,通过两轮步长调整得到最佳的容量补偿价格为17.0×104¥/(MW∙a),即170 ¥/(kW∙a)。当容量补偿价格为17.0×104¥/(MW∙a)时,抽样1 000次计算可靠性指标收敛过程如图5所示,容量补偿价格-可靠性指标关系如图6 所示。此容量补偿价格下2025 年的电源结构与每个机组生命周期内的IRR指标如表3所示。
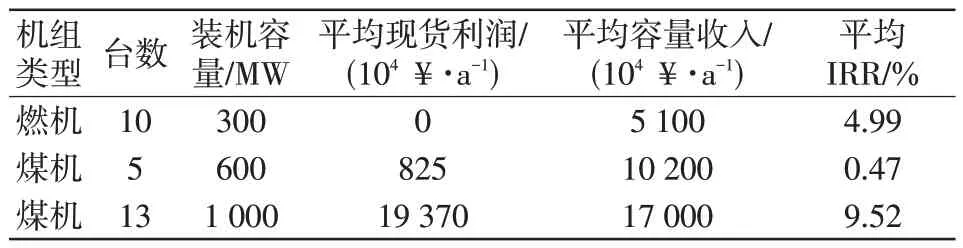
表3 发电机组类型及IRRTab.3 Types and IRR of generators
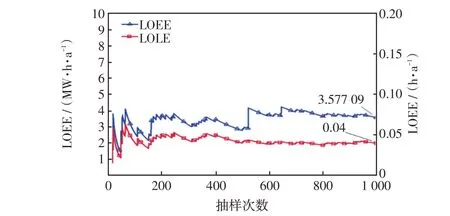
图5 可靠性指标收敛过程Fig.5 Convergence process of reliability index
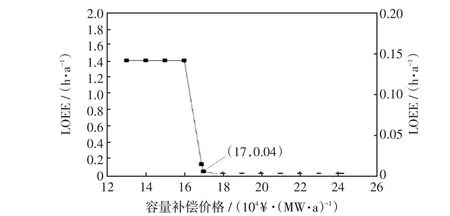
图6 容量补偿价格和可靠性指标关系Fig.6 Relationship between capacity compensation price and reliability index
表4 为采用长期边际成本定价方法和本文容量定价方法的计算结果比较,对比指标包括2025年的发电侧电量费用、发电侧容量费用及可靠性指标,其中发电侧电量费用为所有火电机组的现货市场电能量收入,发电侧容量费用为所有火电机组的容量补偿收入。在采用长期边际成本定价方法时,由于容量补偿价格相对较高,所以2025 年的装机容量更多,现货市场竞争更激烈,使得平均现货价格下降,发电侧电量费用也相对较低。在考虑容量费用后,两种方法都满足可靠性标准,本文方法发电侧总费用减少了21.91×108¥,根据算例系统的用电量,相当于2025 年用户平均购电成本降低了0.019 85 ¥/(kW∙h)。结果表明,本文方法可以在保证电力系统可靠性的同时,最大程度保证电力用户经济性。

表4 两种定价方法计算结果对比Tab.4 Comparison of calculation result between two pricing methods
同时,为了分析高比例风光装机占比对容量补偿价格的影响,在上述算例的基础上,将原有风光装机占比提高至原有的5倍,并计算此时的最佳容量补偿价格。两种场景下的可靠性指标趋势如图7所示。
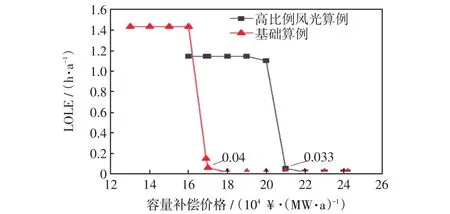
图7 两种场景下的LOLE 指标趋势Fig.7 Trend of LOLE under the two scenarios
从图7可以看出,高比例风光场景下,最佳的容量补偿价格为21.0×104¥/(MW·a),即210 ¥/(kW·a),对应目标年份的可靠性指标LOLE为0.033 h/a。可见,在其他条件不变的情况下,单独增大风电光伏的装机并没有降低容量补偿价格,反而使容量补偿价格得到升高。这是因为风光大规模并网后,使得电力现货市场平均价格下降,压缩了火电机组在现货市场上的利润空间,进而导致需要更高的容量补偿价格才能保证火电机组的正常经营。
4 结 语
本文提出了一种基于可靠性标准的电力现货市场环境下的容量补偿定价方法,以提高电力系统运行的安全稳定,保证容量补偿机制的经济合理性。在定价过程中采用了两阶段容量补偿定价方法,通过算例验证了所提容量补偿定价方法的有效性。结果表明,经过调整后的容量补偿价格可以更经济地实现目标年份的可靠性标准,同时高比例风光并网并不能有效降低容量补偿价格,反而因为其拉低电力现货市场价格,导致传统火电机组需要更高的容量补偿收入才能回收成本,进而使得容量补偿价格高于低比例风光场景。
未来容量补偿定价方法仍需要不断改进,例如如本文为简化机组决策,设定所有机组的投产年限相同,在未来可以考虑各机组不同的投产年限;机组决策模型在进行机组投资/退役时可以考虑更多的经济指标;在计算目标年份可靠性指标时进一步考虑新能源出力的随机特性等。

