“瞻前”又“顾后”，“体验”再“感悟”

摘 要：策略的形成是一个循序渐进的过程，教师在教学中要秉持“大策略观”，瞻前顾后地教策略：发现相应策略在之前教学中的增长点，即“瞻前”；发现教材为后续策略教学提供的孕伏点，即“顾后”，从而巧妙衔接，有机渗透，让学习的过程有根基、有联系。此外，教师应提供探索空间，帮助学生加深策略体验；配置丰富习题，帮助学生发展策略意识；重视回顾反思，帮助学生感悟策略价值。

关键词：小学数学；解决问题的策略；列举

苏教版小学数学教材从三年级上册开始编排“解决问题的策略”单元，旨在让学生形成解决问题的一些基本策略，体验解决问题方法的多样性。不少教师在教学某一“解决问题的策略”单元时，通常是借助教材的例题与习题完成相应的教学任务。由于教材内容相对独立，因此该单元学习后，相应的策略也就被束之高阁。其实，跳出独立单元纵观整套教材，我们会发现，独立单元并不独立，它与其他教学内容有着千丝万缕的联系。因此，教师要能够发现相应策略在之前教学中的增长点，即“瞻前”；还要善于发现教材为后续策略教学提供的孕伏点，即“顾后”，从而巧妙衔接，有机渗透，让学习的过程有根基、有联系。教学五年级上册《解决问题的策略——列举》一课，笔者尝试瞻前顾后地教策略。

一、教学过程

（一）“瞻前”

1.回顾旧知

师 这节课我们学习解决问题的策略，以前学习过吗？有哪些？

（学生回顾、交流。教师梳理并板书：从条件出发、从问题出发、列表、画图……）

看似简单的课前回顾，意在唤醒学生对解决问题的策略的学习经验，同时，多种策略的呈现，也为新知的探索做好了铺垫。

2.拓展情境

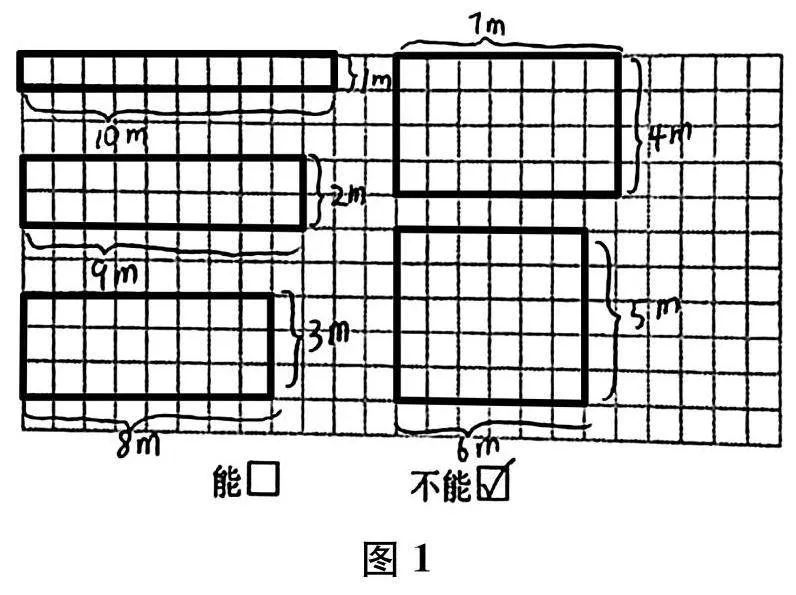
师 王大叔用22根1米长的木条围一个长方形花圃，面积是20平方米，可能吗？

生 应该可以吧？

生 好像不可能。

师 看来还不太确定。通过理解题意，你能想到什么？

生 长方形周长是22米。

师 还能想到什么？

生 长加宽的和是11米。

师 结合已有的解决问题的策略的学习经验，你打算如何解决这个问题？

（学生同桌交流，在作业纸上尝试完成。）

将教材例题“怎样围面积最大”调整为“面积是20平方米，可能吗”，首先避免了部分学生跨越列举过程直奔结论的误区；其次，问题更加聚焦，能够激起学生想方设法地寻找面积是20平方米的长方形；再次，引导点到为止，充分放手，鼓励学生运用已有的策略经验去尝试解决新问题，这既是对已学策略的巩固应用，也是对新问题的积极挑战。

3.对比总结

（学生汇报展示，全班交流。）

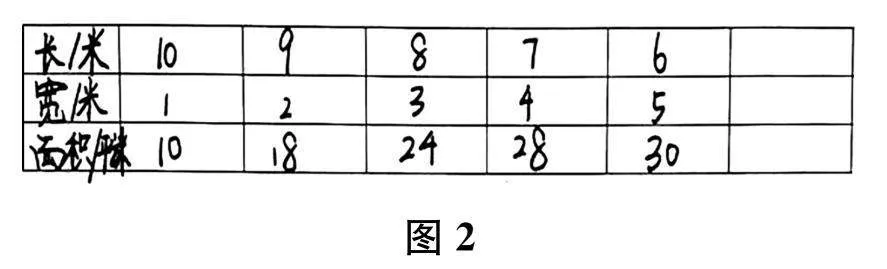
生 （展示做法，如图1所示）因为长加宽的和是11，我就将符合条件的长方形都画了出来，并计算出面积，发现不可能围成面积是20平方米的长方形。

生 （展示做法，如图2所示）我的想法和他差不多，我是列表解决的。

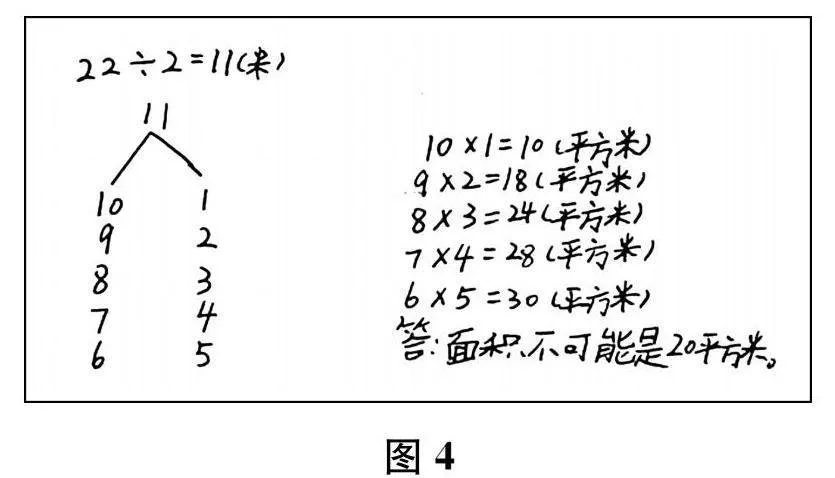
生 （展示做法，如图3所示）我也是列表解决的。

师 这两位同学用的列表方法有什么不同？

生 后一张表里的数据有点乱，最后两组是同样的长方形，重复了。

生 还有一组长8米、宽3米的情况遗漏了。

师 对于这样的情况，你们有什么建议？

生 按顺序写，这样就不会重复，也不会遗漏了。

（教师板书：有序、不重复、不遗漏。）

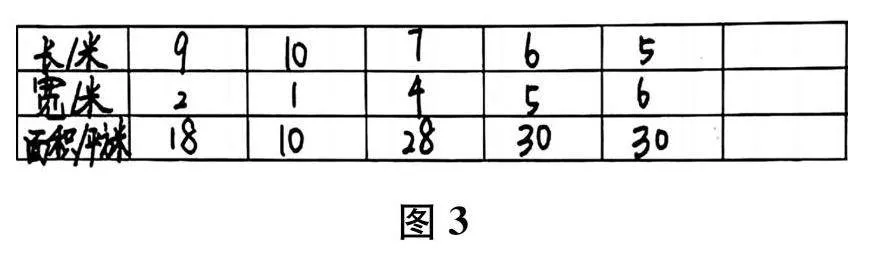
生 （展示做法，如图4所示）我直接列式计算的。

师 你们觉得怎么样？

生 我觉得他的思考和前面三位同学其实是一样的，只是他直接在头脑中想好了长与宽，再进行计算。

生 （展示做法，如图5所示）这是我列的表格。

师 这份表格与前面的不太一样，谁能看明白？

生 前面都是从条件出发，根据长加宽的和是11米，把所有的情况都写下来，看面积有没有20平方米的。他是从问题出发，把长×宽=20的所有情况都写出来，看周长有没有符合22米的。

（全班自发地鼓掌。）

师 刚才同学们运用以前学习过的不同策略，都解决了问题。比较一下，解决问题的过程有什么共同之处？

生 都是把所有情况全部写出来。

师 是的，把符合要求的所有情况逐一罗列出来，这也是一种解决问题的策略，（板书课题）叫作列举。列举策略陌生吗？

生 不陌生，我感觉它和我们以前学习的画图、列表等策略是紧密联系的。

师 是的。在过去的学习中，其实我们也运用过列举的策略解决问题。

（教师带领学生回顾。）

策略的形成过程不能是生拉硬拽地直奔目的地，而应是在已有策略经验的基础上为了达成新的目标自然生长出来的。通过对解决问题不同方式的充分展示、交流、对比，引导学生逐渐提炼出新策略的共性，就是逐一罗列（列举）；同时，通过对同类方式不同结果的辨析，引导学生感受列举时要有序进行，才能做到不重复、不遗漏。

（二）“烧中段”

师 下面我们来玩一个游戏：红包雨。有1元、5元、8元三种币值的红包，每个参与者有两次点击机会，运气不好可能空门哦！

（教师指名学生上台玩“红包雨”游戏。）

师 你能说出一个参与者可能得到的红包金额是多少吗？

（学生列举：点中0次，0元；点中1次，1元、5元、8元；点中2次，2元、6元、9元、10元、13元、16元。）

策略的应用不仅在解决数学问题中，更可融入学生感兴趣的生活情境中。“红包雨”游戏，激起学生强烈的学习热情。由于游戏的结果情况相对复杂，学生首先根据点中红包的次数进行分类，再列举；在点中两次红包的情况中，学生又进行了二次列举。在充满挑战性的活动中，学生充分体验到列举过程中有序的重要性。

（三）“顾后”

师 经过研究，王大叔发现用22根1米长的木条，不可能围成面积是20平方米的长方形花圃。他对列举出来的情况又进行了仔细的研究，（出示表1）有了一个惊喜的发现？你们知道是什么吗？

生 长和宽越接近，面积越大。

生 我补充，要在周长不变的情况下。

师 有了这个发现，王大叔又有了新的打算。他打算用24根1米长的木条围一个长方形菜园，怎样围面积最大？

生 长加宽的和是24÷2=12（米），当长和宽都是6时，面积最大，也就是6×6=36（平方米）。

生 也就是说，在周长一定的情况下，围成正方形的面积最大。

师 这次你们列举了吗？

生 没有。运用刚才列举得到的结论，可以直接得到答案。

列举策略的使用，不仅能够直接找出答案，同时能够发现规律。课尾，设计王大叔围菜园的问题，不仅与课始王大叔围花圃的问题呼应，同时因为有了对规律的发现与应用，学生不再列举出所有情况，而是直接应用结论解决问题。这样的过程，既是思维的提升，也是策略价值的升华。

二、教学反思

（一）提供探索空间，加深策略体验

解决问题的策略是以具体问题为载体的，学生在充分的问题解决过程中形成策略。因此，问题的设计就显得尤为重要。许多学生在学完策略后，不愿意用策略。

一是因为要解决的问题相对简单，学生不愿意给自己额外增加负担；二是因为问题的呈现并未激发起学生的内在需求。因此，创设有趣的、有挑战性的问题场景，让学生进入一时无解却又特别想解的愤悱状态，激发策略学习的内需。

开放的解决路径有利于促进多元思考。相比于教材中的问题“怎样围面积最大”，调整后的问题“围成20平方米的花圃，可能吗”更为聚焦，思路更加开放。学生可以从条件想起，借助周长是20米，先得到长加宽的和是11米，再将长和宽的情况列举出来；也可以从问题出发，先将满足面积是20平方米的情况列举出来，再将长与宽的和相加，与11米逐一比对。同时，呈现的形式可以是画图、列表，还可以是算式。开放的问题设置为学生提供了充分的探索空间，学生借助已有的策略经验来列举，充分体验策略的应用过程。

深入的共性提炼有利于学生理解策略本质。多元化的思维呈现让学生有了充分的活动体验，也为列举策略本质的提炼提供了充分的依据。教师引导学生观察各组解决问题的过程，发现无论画图还是列表，都是将符合要求的所有可能逐一罗列出来；通过对不同列表方法的对比，发现问题。学生由衷地体会到列举时“有序”的重要性，有效地训练了思维的条理性和严密性。

（二）配置丰富习题，发展策略意识

策略不是无源之水、无本之木，而是在解决问题的过程中不断体验、积累而形成的。策略意识的形成需要不断地深耕培育，让萌芽不断茁壮成长。教材中呈现的例题都是经过精心选择的，但仅仅依靠教材中的题目还远远不够，需要更加丰富多元的习题配置帮助学生发展策略意识。一是设置挑战性的问题，激发学生运用策略解决问题的内需。二是设置生活化的问题，如王大叔围花圃、围菜园，通过解决实际问题，促进学生自觉运用策略，发展策略意识。三是设置实践性的问题，如“红包雨”游戏，让学生动手参与、动脑思考，主动地运用策略解决问题。

（三）重视回顾反思，感悟策略价值

反思是一种内省行为，是对已有认知的再认识，是对已有体验的再回顾。在解决问题的策略的教学内容中，有一个重要板块是回顾反思。在解决问题的策略的教学中，“解决问题”和“策略”是紧密结合、不可分割的两个目标，学生在解决问题之后，教师可以引导学生反思：为什么要用策略？怎样用策略？策略有什么好处？比如，学生在用画图、列表、算式等多种方式将结果逐一罗列之后，反思这些方法的相通之处，发现列举的本质特点，让新策略在原有学习经验的基础上自然生长。再如，课尾，学生对列举的长和宽以及面积进行研究后，发现了“周长一定时，长和宽越接近，面积越大”的规律，使自己对策略的认识和理解进一步升华，感受到策略不仅可以直接解决问题，还能发现规律，进而将结论直接应用于同类问题的解决中，思维水平得到了明显提升。

策略的形成是一个循序渐进的过程，教师在教学中要秉持“大策略观”，瞻前顾后地实施策略教学，引导学生经历学习过程，反思学习体验，促进学生体验策略、理解策略、应用策略、拓展策略，从而提升数学素养和解决问题的能力。

1-6，12-13，17-18，21，26，34，36，42，46，48-50，52，63，64，78，81，84，87，88