利用“结构性情境”促进学生提出问题

摘 要：《长方形和正方形》单元复习课，依据“问题提出”的教学理念，设计“用小棒拼图形、求周长”的结构性情境，引导学生提出问题，进而梳理、解决所提问题，从而使学生清楚地认识到边是理解图形及其周长的关键，能抓住部分与整体的关系理解几何概念的本质。具体地，分三个环节，变化情境的要素，提出不同的任务要求，实现全面梳理单元知识、逆向思考边长与周长的关系、拓展应用图形及其周长的知识等教学目标。

关键词：小学数学；问题提出；结构性情境；《长方形和正方形》

本文系蔡金法教授团队的小学数学“问题提出”教学课例系列文章之一。

一、教学实践

（一）教前思考

人教版小学数学三年级上册第七单元《长方形和正方形》涉及四边形、周长的相关知识，具体包含五道例题：例1是四边形的初步认识，例2涉及长方形、正方形的特征，例3涉及周长的含义，例4是长方形、正方形的周长计算，例5是解决实际问题。此前，学生在一年级下册《认识图形（二）》单元的学习中，直观地认识了长方形、正方形，并且能够辨认和区分这些图形。此后，学生将会在四年级上册《平行四边形和梯形》单元的学习中，从与平行四边形关系的角度进一步认识长方形、正方形。

在多年的教学实践中，笔者发现，本单元学习后，学生对四边形、长方形、正方形、周长等概念是基本能够理解的，但是，对于相关知识的灵活运用还存在一定的问题。例如，对于“四边形的特点”“图形周长的定义”“长方形、正方形周长的计算”等正向思考、直接应用的题目，学生几乎不会出错；但遇到“用两个边长为1厘米的正方形拼成一个长方形，该长方形的周长是多少？”这样的题目，有的学生不知如何下手，答案千姿百态；遇到“在方格纸上围出周长是24厘米的不同长方形”这样的题目，有的学生就一个个去凑，缺乏思考程序。究其原因，是学生对图形及其周长的理解没有联系到图形的边，所以在遇到问题时，不善于抓住图形的边去分析。

因此，本单元的复习课，笔者尝试依据“问题提出”的教学理念，设计“用小棒拼图形、求周长”的结构性情境，引导学生提出问题，进而梳理、解决所提问题，从而让学生有更多的机会思考“什么样的边组合在一起能形成四边形、长方形或正方形等？”“这些图形的周长计算与边的特征又有什么样的关系？”等问题，使学生清楚地认识到边是理解图形及其周长的关键，能抓住部分与整体的关系理解几何概念的本质；同时，及时发现学生不同的学习需求，做好针对性、差异化教学。具体来说，分三个环节，变化情境的要素，提出不同的任务要求（即引导语），实现如下教学目标：（1）全面梳理单元知识，建立单元知识体系；（2）逆向思考边长与周长的关系，发展灵活运用知识的能力；（3）拓展应用图形及其周长的知识，创造更多学习机会。

（二）教学过程

1.全面梳理单元知识

教师出示图1，给出问题情境：“猜想魔术袋中四根小棒长短可能是怎样的，它们能够拼接成怎样的图形，这些图形的周长怎样计算。”并提出任务要求：“在学习单中，用示意图的方式提出关于周长计算的问题并思考如何解决。想到几种情况就提出几个问题。”

学生在情境的引导下，得到了很多四边形，提出了很多关于周长计算的问题。教师巡视后，根据四根小棒不同长短的搭配，引导学生逐步展示各种情况：四根一样长（正方形或菱形）、三根一样长（普通四边形或等腰梯形）、只有两根一样长（普通四边形或等腰梯形）、两根两根一样长（长方形、平行四边形、筝形或“飞镖形”）、四根全不一样长（普通四边形）。然后，引导学生分析相应图形的区别以及周长计算方法，得到如图2所示的汇总结果。

在分析四根小棒不同长短的情况，再把四根小棒拼接成图形的过程中，学生充分感受到各种四边形与其边的关系，以及四边形的不稳定性，不仅复习了包括长方形、正方形在内的各种四边形的特征，能更准确地画出各种四边形，而且巩固了各种四边形（如普通四边形、长方形、正方形）之间的关系（如包含关系、交叉关系），以及周长与边长的关系（周长是各个边长的和）。而在计算四边形周长的过程中，学生不仅明白了各种四边形的特征与周长计算公式的关系，而且理解了特殊四边形周长计算公式的应用价值在于用乘法（而非加法）计算相同长度边的长度和。

因此，在组织学生交流、解决所提问题的过程中，教师渗透了如下考查学生对本单元知识理解的问题，学生给出了很好的解答。

（1）有四条边的图形是四边形，对吗？（不对，四边形是由四条线段围成的封闭图形，因而有四个角）四边形有四条边，对吗？（对）

（2）四条边都相等的四边形是正方形，对吗？（不对，正方形不仅四条边都相等，而且四个角都是直角）正方形的四条边都相等，对吗？（对）

（3）在一个长方形里剪一个最大的正方形，这个正方形的边长就是原来长方形的宽，对吗？（对）

（4）一个长方形，相邻两条边的长度和是24厘米，它的周长是（ "）厘米。（48）

（5）一张桌子长2米、宽1米，其中一边靠墙摆放，其余三边围花边，则花边至少5米，对吗？（不对，至少4米）

2.逆向思考边长与周长的关系

教师出示图3，给出问题情境：“假设最后拼接成的图形周长是16。

”提出任务要求：“在学习单中，提出关于周长计算过程的问题，并写出可能的计算过程再画图验证。想到几种情况就写出几个算式。”

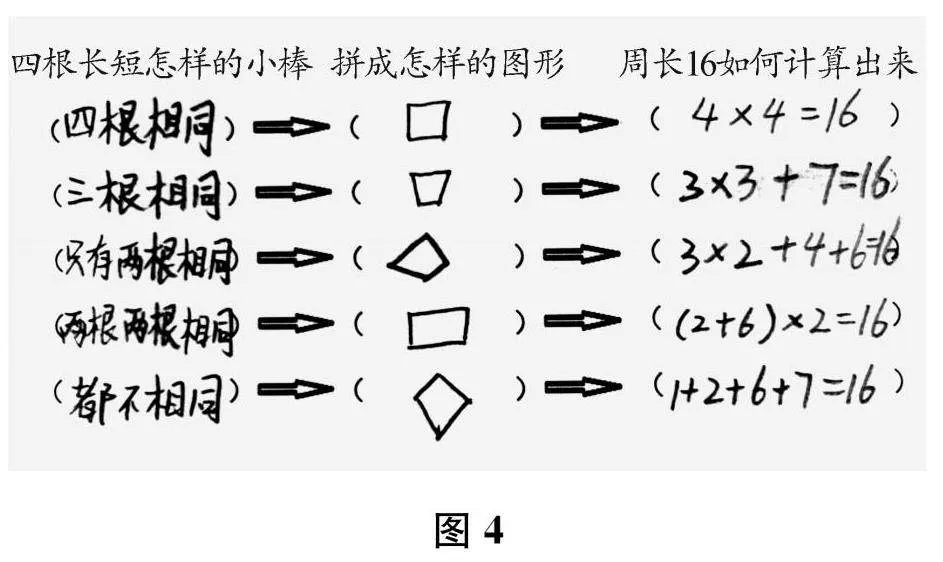
学生在情境的引导下，针对前一环节所分的小棒长短情况，提出相应的关于周长计算过程的问题。教师巡视后，首先针对四根小棒不同长短的搭配，引导学生逐步展示各种情况下一种可能的计算过程，得到如图4所示的汇总结果。然后，通过画图验证，引导学生发现拼接成四边形的必要条件：最长边的长度小于其他三边的长度和（这里就是最长边小于8）。由此，便可以引导学生通过有序思考，不重不漏地找到各种情况下所有可能的计算过程（限定边长为整数）：四根一样长，4×4=16；三根一样长，3×3+7=16或5×3+1=16；只有两根一样长，2×2+5+7=16、3×2+4+6=16、4×2+1+7=16、4×2+2+6=16、4×2+3+5=16、5×2+2+4=16或6×2+1+3=16；两根两根一样长，（1+7）×2=16、（2+6）×2=16或（3+5）×2=16；四根全不一样长，1+2+6+7=16、1+3+5+7=16、1+4+5+6=16、2+3+4+7=16或2+3+5+6=16。

在上述“由周长求边长”的活动中，学生对周长的定义以及长方形、正方形的周长计算公式进行了逆向运用，发展了逆向思维；还挑战了“不重不漏地找出所有可能的计算过程”的任务，学会了有序思考；同时，发现了四边形四边长度之间的关系，加深了对周长与边长关系的理解，进一步体会到四边形的不稳定性。

3.拓展应用图形及其周长的知识

教师出示下页图5，给出问题情境：“现在，魔术袋中小棒的根数也不确定，

猜想它们能够拼接成怎样的图形，这些图形的周长怎样计算。”提出任务要求：“在学习单中，用示意图的方式提出关于组合图形或不规则图形周长计算的问题并思考如何解决。想到几种情况就提出几个问题。”

学生在情境的引导下，更加自由地设计（拼接），得到了丰富的组合图形或不规则图形（实际上，可能的图形是无限的），提出了更多关于周长计算的问题。

教师巡视后，首先根据图形的类型，比较全面地展示学生提出的问题，以及解决问题的思路（如图6所示，包括两个正方形或菱形的组合、两个长方形或平行四边形的组合、四个长方形或平行四边形的组合、多或缺一块或几块的长方形、内有曲边的长方形等情况）。

然后，改编呈现学生提出的长方形、正方形组合或“多缺”问题，引导学生解决。具体问题如下：

（1）两个完全一样的正方形能拼成一个长方形吗？（能）两个完全一样的长方形能拼成一个正方形吗？（不一定能）

（2）将6个长3厘米、宽2厘米的长方形拼成一个长方形或正方形，可以怎么拼？拼成的图形的周长最长是多少厘米，最短是多少厘米？（有4种拼法。可以用小图形周长之和减去重叠的边长，也可以用周长的定义直接计算大图形的周长。小图形之间重叠的边长越大，大图形的周长越小。）

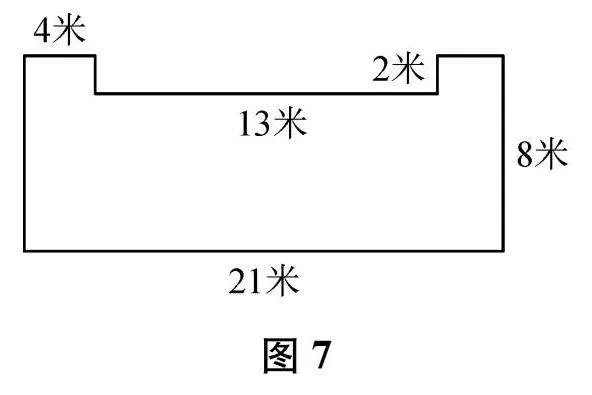
（3）如图7，求该图形的周长。［21×2+8×2+2×2=62（米），4米和13米是多余条件］

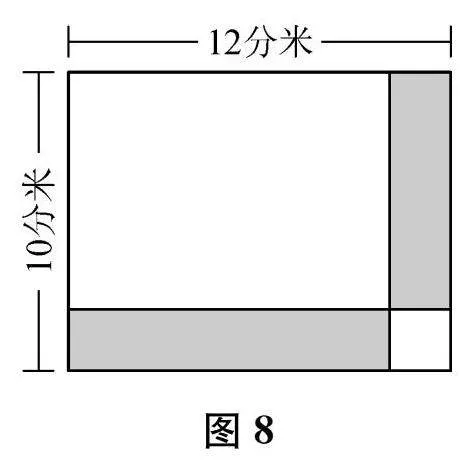
（4）如图8，求图中阴影部分的周长。［12×2+10×2=44（米），利用平移的方法］

（5）如图9，每组的两个图形，周长都一样吗？（第一组一样，第二组不一样，第三组一样。利用平移、不看公共部分等方法）

在上述拓展的“拼图形、求周长”活动中，学生创造出丰富的图形，并结合图形的特征求图形的周长，获得了充分的学习机会和不同层次的发展，深化了对长方形、正方形特征以及周长概念、计算的认识，进一步认识到掌握图形特征和周长计算的关键是抓住图形的边去分析。

二、教学评析

在“问题提出”教学中，如何设计情境，来激发学生数学探索的内在动机，让学生提出有价值的数学问题，是难点所在。俞波老师的这堂课在这方面进行了很多有价值的探索。

一开始，俞老师基于“四根长短怎样的小棒—拼成怎样的图形—周长如何计算”的框架设计情境，让学生通过动手操作用填空的方式完成问题提出。这种问题提出的情境结构性比较强，更适合低年级的学生，尤其是对还不清楚如何提出有效的数学问题的学生特别有帮助。

这一框架还蕴含着关于本单元知识重要的三个命题之间抽象的逻辑关系：四边形边长特征

—不同四边形的名称—它们的周长计算方式。因为整个探索过程是通过实物操作完成的，学生在问题提出的过程中，就开始体验和关注到三者之间的逻辑关系。

有意思的是，组织学生完成了第一个问题提出活动后，俞老师利用类似的框架，通过增加一个条件（固定周长为16）设计情境，开启了第二个问题提出的活动。这个设计非常巧妙，不仅和第一个活动有合理的连接，更重要的是能引导学生进一步关注四边形边长和周长计算之间的关系。如果说第一个问题提出活动可以帮助学生理清“四边形的边长特征—不同四边形的名称—周长计算公式”这一顺向的逻辑关系，第二个问题提出活动则是帮助学生探索三者之间的逆向逻辑关系。

组织学生完成了第二个问题提出活动后，俞老师改变了第一个情境中小棒的数量，进一步激发学生对多边形形状和周长关系的探索。布朗和瓦尔特在1990年出版的专著《提出问题的艺术》中提出了“否定假设法”，也就是“如果它不是这样的，那又可能是什么”策略。这是从原问题出发，产生新问题的一种方法。显然，俞老师的问题提出情境设计是这一思想的体现。

本堂课中，俞老师基于结构性情境，利用三个联系紧凑的问题提出活动，让学生不断深化对知识的探索。这犹如一套漂亮的组合拳，直击教学难点。