随机两体耗散诱导的非厄米多体局域化*

刘敬鹄 徐志浩2)†

1) (山西大学理论物理研究所,量子光学与光量子器件国家重点实验室,太原 030006)

2) (山西大学极端光学协同创新中心,太原 030006)

本文数值研究了在一维非厄米的硬核玻色模型中由随机两体耗散诱导的非厄米多体局域化现象.随着无序强度的增强,系统的能谱统计分布从AI† 对称类向二维泊松系综过渡,多体本征态的归一化参与率展示了从有限值到接近零的转变,半链纠缠熵服从体积律到面积律的转变,动力学半链纠缠熵表现为从线性增长到对数增长的转变.数值结果表明,在该模型中由随机两体耗散诱导的非厄米多体局域化现象的鲁棒性.该研究结果为非厄米系统中多体局域化的研究提供了新的视角.

1 引言

多体局域化揭示了多体无序系统中存在稳定的局域态,彻底改变了人们对量子系统的理解[1-11].作为安德森局域化[12,13]的重要延伸,多体局域化提供了量子多体系统保持非热平衡态的例子[14-18],它可以由许多序参量来表征.例如,呈泊松分布的能级统计分布[19,20]、随时间对数增长的纠缠熵[21,22]、本征态纠缠熵的面积定律[23,24]、有限的非平衡占据数[25,26]、可积性的出现[27,28]等.因为其在量子存储和可控动力学等领域存在潜在的应用前景,在实验和理论方面引起了广泛的关注[25,29-33].目前,已经在很多平台上实现了多体局域相关的实验,包括超冷原子[29,30]、离子阱[32]和超导电路[25,33]等.

传统的量子力学是基于厄米性的假设,即厄米算符代表物理可观测量.这个假设保证了这些算符的本征值是实数,相应的本征矢满足正交归一性[34,35].然而,近年来,理论和实验的研究已从厄米系统推广到非厄米系统,并涌现出一系列新奇的非厄米现象及其应用,如非厄米趋肤效应[36,37]、边界依赖的能谱[38]、体-边对应关系的失效[39,40]和非布洛赫能带理论[41-43].最近在非厄米系统中引入无序,为局域化现象的研究开辟了新的视角.最早由Hatano和Nelson[44-46]把在位无序势和非互易跃迁引入到单粒子格点模型中,揭示了非互易会诱导出安德森局域化转变,同时伴随着单粒子谱的实-复转变和拓扑相转变的独特现象.Hamazaki 等[47]将这一问题扩展到了多体系统中,在具有时间反演对称性的非互易晶格模型中存在非厄米多体局域化,并且发现了局域化转变和谱的实-复转变一致.另外在时间反演对称性破缺的非厄米无序和准周期系统中也发现存在多体局域化现象[48-50].非厄米效应可以在许多实验平台实现,特别是最近通过可控的两体非弹性散射,在玻色哈伯德模型中实现了复相互作用[51,52].Wang 等[53]讨论了利用光学Feshbach 共振实现复散射长度的可行方案.本文考虑一个具有随机两体耗散的一维非厄米的硬核玻色模型,发现在强无序区域系统存在非厄米多体局域化现象.该研究对理解非厄米多体局域化有重要意义.

2 理论模型

本文考虑一个具有随机两体耗散的硬核玻色子模型,其哈密顿量为

本文考虑半填充的情况,即总粒子数N=L/2,相应的希尔伯特空间维度为D=.选取J为能量单位,即J=1,且U=0.25 为例进行讨论.本文中,对于序参量的平均需要考虑两重平均,标记为,其中上横线表示无序的平均,选取无序的样本数为Nsample=1000(L=6,8,10),Nsample=500(L=12)和Nsample=100(L=14),〈···〉表示对能级的统计平均,这里仅考虑能谱中心处 1/5 范围内的能级.

3 数值结果

能谱统计行为作为研究多体局域化的主要手段之一被广泛应用.厄米情况下,随机矩阵理论[3,54-57]指出,当系统处于混沌或遍历相时,能谱统计呈现高斯分布.根据系统的对称性,分为高斯酉系综(Gaussian unitary ensemble,GUE)、高斯正交系综(Gaussian orthogonal ensemble,GOE)和高斯辛系综(Gaussian symplectic ensemble,GSE),分别对应于A 对称类、AI 对称类和AII 对称类的系统.然而,当系统处于可积或多体局域相时,能谱的统计分布遵循泊松统计.在非厄米情况下,混沌或遍历相也存在3 种普适类: A 对称类、AI†对称类和AII†对称类[58-60],而可积或多体局域相的泊松统计推广为二维泊松统计.

为了研究非厄米系统复能谱的统计行为,复平面上的最近邻能级间距定义为d1,i=minj|Ei-Ej|,其中Ei是系统的本征能量[58].由于不同系统具体性质不同,导致局域平均密度存在差异,使得直接对d1,i的统计并不具备普适性.为了消除这种由局域平均密度差异带来的影响,对d1,i进行重整化处理,即si=,其中是局部平均密度,要求足够大且远小于D,这里选取≈30,并且dn,i表示Ei和其第n级近邻能级的距离.然后对能级间距si进行归一化,其满足=1.通过将分布函数p(s) 与相应对称类的非厄米随机矩阵进行对比,可以直观地反映出非厄米多体局域化转变的发生.根据非厄米系统的对称性分类,哈密顿量(1)满足H=HT,属于AI†对称类,系统的统计行为可由相应的非厄米随机矩阵来刻画[58-62].对于最简单的A 对称类系统,最近邻能级间距的统计分布遵循Ginibre 酉系综(Ginibre unitary ensemble) 分布:

如图1 中黑色虚线所示.相比之下,AI†(AII†)对称类的分布与A 类不同,即峰值低于(高于)PA(s).虽然目前对于任意尺寸的AI†和AII†对称类分布没有解析表达式,而小尺寸情况下AI†对称类具有确定的表达式[58]:

图1 当L=14 时,哈密顿量(1)式平均的最近邻能级间距s 的统计分布 (a) W=2;(b) W=20.黑色虚线、红色实线和绿色点线分别表示A,AI † 类和二维泊松分布Fig.1.Mean unfolded nearest-level-spacing distributions of the Hamiltonian Eq.(1) with L=14: (a) W=2;(b) W=20.Black dash,red solid,and green dotted lines represent A,AI † classes,and two dimensional (2D)-Poisson distributions,respectively.

图2 当L=14 时,平均的径向强度分布 和相应的幅角分布 (a),(b) W=2; (c),(d) W=20 .红色实线是通过统计对应的随机矩阵 (1000×1000)的结果,其无序次数选取为1000.(e),(f)径向强度的平均值 和相应的幅角的平均值随无序强度变化曲线.上(下)虚线对应于AI † 对称类(2D-Poisson)统计极限值,≈0.722,≈0.193 (=2/3,=0)Fig.2.(a),(b) Mean marginal distributions and with W=2 for the complex energy spectrum for L=14 ;(c),(d)the marginal distributions and with W=20 for the complex energy spectrum.The red solid lines are obtained by calculating and of the 1000×1000 random matrices with the corresponding random matrix ensembles averaged 1000 realizations.(e),(f) The averages and as a function of the disorder strength W.The upper (lower) dash line corresponds to the AI† symmetry class (2D-Poisson) expectation,≈0.722, ≈0.193 (=2/3,=0).

其中Kν(x)=是修正的贝塞尔函数,C2==1.16187··· 是一个常数,如图1 中红实线所示,Γ 表示伽玛函数.当无序强度W=2 时,平均的最近邻能级间距s的分布满足AI†对称类(图1(a)).当无序强度W=20时,其与二维泊松分布(绿色点线)一致(图1(b)).二维泊松分布数学形式如下:

本文对能谱的统计考虑能谱中心1/5 的范围内的能级.图1 的结果表明,在强随机两体耗散时,系统进入非厄米多体局域相.

为了进一步验证非厄米多体局域化的转变,可计算复能级差比率(complex spacing ratio,CSR),其定义为[59,60,63,64]

归一化的参与率(normalized participation ratio,NPR) 也可以用来衡量多体局域化的发生,其定义为[66]

其中 |ψi〉是本征值Ei对应的本征态,|n1,n2···,nL〉表示在粒子数表象中的Fock 基矢.在热力学极限下,如果本征态是遍历态,η为有限值.如果本征态是多体局域态,则η趋近于0.为了便于讨论,这里考虑一次无序构型下,系统所有本征态的η,并且把系统的本征能量进行重整化处理:

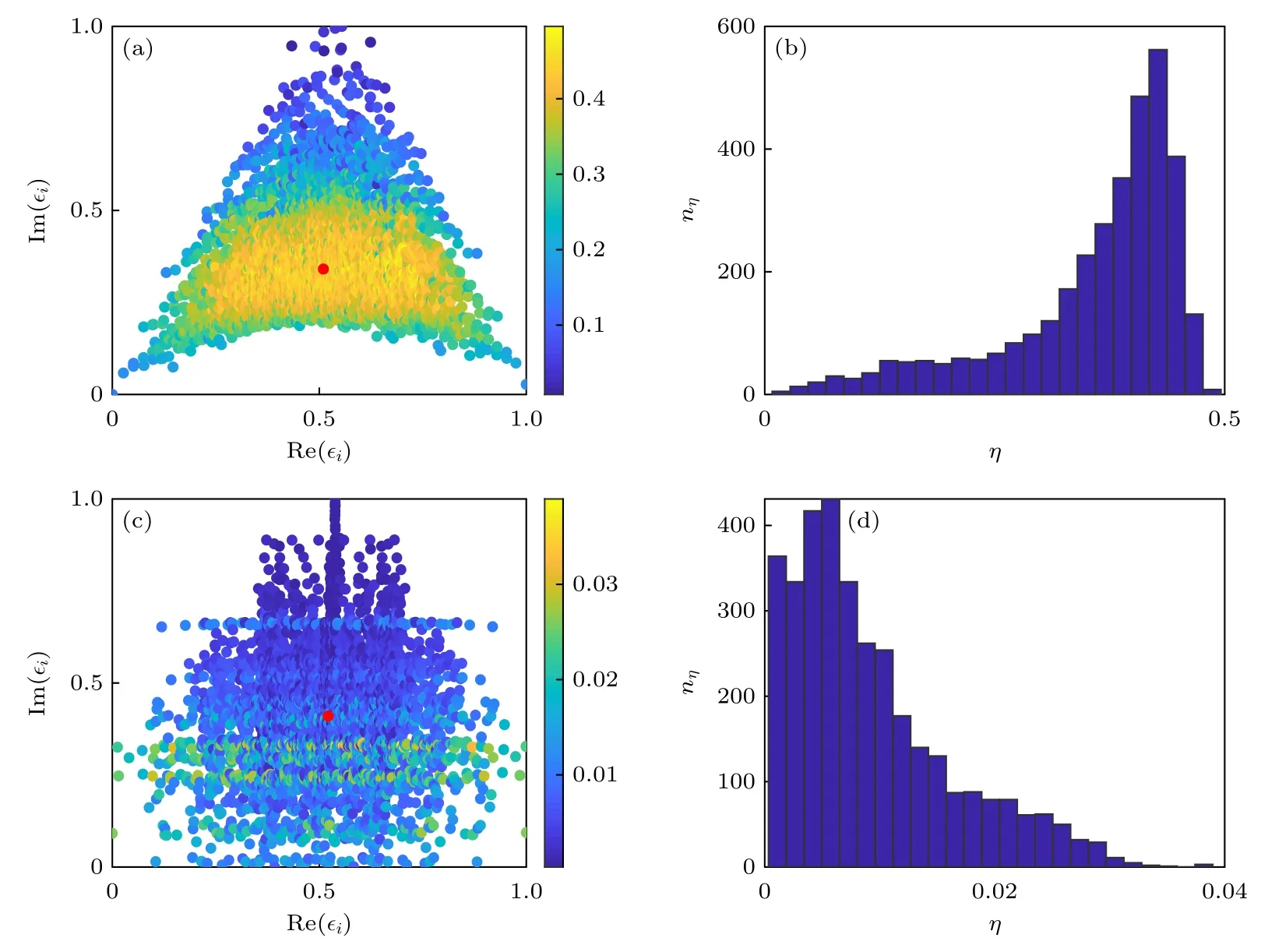
图3 当 L=14 时,在复平面上,系统所有本征态的 η 随重整后能谱 εi 的分布情况(红点表示能谱的中心) (a) W=2;(c) W=20 .归一化的参与率 η 统计直方图 (b) W=2 ;(d)W=20Fig.3.Distribution of η for all eigenstates versus the rescaled spectrum εi with L=14 (Red dots represent the center of the energy spectrum): (a) W=2;(c) W=20.Histogram of the normalized participation ratio η:(b) W=2;(d) W=20.

此外,还计算了多体本征态的半链纠缠熵(half-chain entanglement entropy),定义为S=-Tr[ρL/2lnρL/2]=,其中,λm是约化密度矩阵ρL/2的第m个本征值.ρL/2可以通过对系统半链的自由度求迹获得,即ρL/2=TrL/2[|ψi〉〈ψi|].图4(a)展示了不同的系统尺寸 (L=10,12,14)下平均的半链纠缠熵随无序强度的变化.在弱无序时,系统尺寸越大,越大.随无序强度增强,不同尺寸的均减小,最终趋于重合.该结果表明,在弱无序时,正比于系统尺寸,而强无序情况下,其对系统的尺寸变化不敏感.平均的半链纠缠熵展现了从体积律到面积律的转变行为.

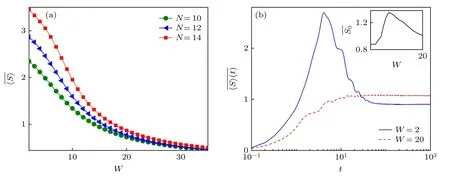
图4 (a)不同尺寸下,平均半链纠缠熵随无序强度的变化;(b)当 L=14 时,不同无序强度W 对应的随时间的演化.初态为 |ψ0〉=|1010···〉.插图展示了平均稳态熵 随无序强度的变化Fig.4.(a) Mean half-chain entanglement entropy as a function of the disorder strength W for different L;(b) the dynamics of the mean half-chain entanglement entropy for different W with L=14.The initial state is taken as |ψ0〉=|1010···〉.The inset displays the mean steady-state entanglement entropy as a function of W.

平均的半链纠缠熵的动力学演化也可以表征系统多体局域化的发生,其定义为

其中ρL/2(t)=TrL/2[|ψ(t)〉〈ψ(t)|] 是t时刻半链的约化密度矩阵.这里的 |ψ(t)〉是任意时刻的波函数,其表示为

4 总结

本文研究了随机两体耗散诱导非厄米多体局域化现象.在弱无序时,系统处在遍历相,能谱统计满足AI†对称类分布,与系统所满足的对称类一致,而在强无序情况下,系统处在多体局域相,其能谱统计满足二维泊松分布.通过计算归一化的参与率,发现在遍历相中,大部分本征态的归一化的参与率是有限值,而在多体局域相中,大部分归一化的参与率接近于零,并且系统平均的半链纠缠熵随无序的增强从体积律到面积律转变.短时内动力学半链纠缠熵的线性和对数增长的演化行为,进一步验证了系统遍历相和非厄米多体局域相的存在.长时极限下,动力学半链纠缠熵趋向于系统稳态的半链纠缠熵.本文的研究为非厄米系统多体局域化现象的研究提供了参考.