基于里德伯原子天线的低频电场波形测量*

张学超 乔佳慧 刘瑶 苏楠 刘智慧 蔡婷 何军4)† 赵延霆 王军民4)

1) (山西大学光电研究所,量子光学与光量子器件国家重点实验室,太原 030006)

2) (山西大学物理电子工程学院,太原 030006)

3) (山西大学激光光谱研究所,量子光学与光量子器件国家重点实验室,太原 030006)

4) (山西大学,省部共建极端光学协同创新中心,太原 030006)

里德伯原子的高极化率可以实现电磁场的多维度参数测量.本文利用室温里德伯原子构建原子天线,基于原子天线将低频电场幅度信息转化为强度信息,从而实现低频电场的参数测量.实验采用双光子激发制备铯原子里德伯态,通过阶梯型电磁感应透明(electromagnetically induced transparency,EIT)光谱实现里德伯原子量子态的检测,基于内置电极技术在室温原子气室导入kHz 频段低频电场.电场中里德伯原子的Stark 频移会在EIT 过程导致双光子失谐,从而引起EIT 光谱频移和强度变化.在弱电场条件下,EIT 光谱频移可以忽略,EIT 透射强度与输入低频电场强度近似为线性关系,基于该效应可以实现低频电场的波形、幅度、频率等参数测量.

1 引言

低频电场是指频率在几百赫兹到千赫兹之间的电场信号.该频段电磁场具有波长较长、能量较低的特点,其在天文地理、生物医学、通信工程等众多科学研究领域具有广泛应用.在天文研究中,低频电场可用于探测星际介质的物理性质和结构;在地球物理研究中,低频电场可以用于研究大陆、海洋环境的电磁波传播和散射规律,这在广域搜索、广域信标定位等领域应用潜力巨大;在生物医学研究中,通过低频电场的幅度、波形等参数控制可以调控神经元活动,这是大脑功能和结构研究的重要手段;在电力传输工程应用中,通过设备区域低频电磁场的强度和波形参数监测,可以用于电力系统安全检测和安全预警.这些研究需要对电磁场的波形、幅度、频率等参数进行精确测量,因此,低频电磁场的多维度参数测量方法和测量精度至关重要.

传统低频电场测量手段主要包括电感耦合和电容耦合[1-3].相关技术在低频电场的幅度测量方面比较成熟,但在波形识别和绝对量值测量方面存在困难[4].由于低频电场波长较长,传统滤波放大方法往往无法兼顾低频电磁场的高频特性,电场畸变会导致波形识别不准确、系统动态特性测量困难等问题[5].近年来,研究人员提出利用里德伯原子构建原子天线开展电磁场参数测量[6-10],基于原子天线的测量方法可以将电磁场的场强测量通过光谱技术转换到频率测量上,实现电磁场量值溯源,因此原子天线技术广泛应用于电磁场参数测量领域.

里德伯原子是主量子数较大的高激发态原子,其具有较大的极化率和电偶极矩,对电磁场十分敏感[11,12].基于里德伯原子的电场测量在过去几十年里发展迅速.2012 年,Sedlacek 等[6]在国际上首次报道了基于里德伯原子的微波电场测量,实验获得的最小场强约为8 μV/cm,灵敏度约为30 μV/(cm·Hz1/2).该灵敏度比传统可溯源至国际标准单位制的微波电场计高了将近2 个数量级.2017 年,该研究组基于频率调制技术将测量灵敏度提高到约3 μV/(cm·Hz1/2)[13].Gordon 等[14]于2019 年基于原子天线的差拍探测技术获得了790 nV/(cm·Hz1/2)极限灵敏度;2020 年,Jing 等[15]基于原子天线的超外差技术将微波场强测量的灵敏度提高到55 nV/(cm·Hz1/2).2022 年,Ding等[16]利用里德伯原子多体系统相变方法实验实现49 nV/(cm·Hz1/2)的极限灵敏度.2023 年,Cai等[17]利用优化的幅度调制技术实现了5.102(49)nV/(cm·Hz1/2)的极限灵敏度.

上述工作主要集中于GHz 频段的电磁场测量.由于室温原子气室的屏蔽或衰减效应,MHz 以下的低频电磁场很难进入气室传感区域,该频段电磁场测量较为困难[18-20].为了解决室温原子气室的低频电场屏蔽效应,2012 年,Carter 等[21]通过内置电极的冷原子系统实现材料表面的电场测量,实验测量的电场值为0.6 V/cm.Hankin 等[22]于2014 年利用冷原子测量真空系统直流电场,研究利用激光控制掺锡氧化铟(ITO)薄膜产生可控电场以补偿真空系统的背景静电场,实验可测量的典型电场强度为1.5 V/cm.2020 年,Jau 和Carter[20]利用蓝宝石材料制造热原子气室以减弱气室低频电场屏蔽效应,通过原子气室内部电场光学调控优化原子电场敏感态,在kHz 分析频率频段获得的极限灵敏度约0.34 mV/(cm·Hz1/2).2020 年,Ma等[23]利用激光对气室内部电荷调节改变气室电学特性,基于里德伯电磁诱导透明光谱测得电场值为0.8 V/cm.

基于内置电极技术结合波导技术,可以实现宽频段电磁场测量.2020 年,Meyer 等[12]利用微带波导耦合里德伯原子传感器,实现0—20 GHz的极限灵敏度测量,实验演示了对中频、甚高频、2.4 GHz 蓝牙、WIFI 等无线电信号的测量.2020 年,Bai 等[24]基于冷原子系统,通过单光子激发制备特定轨道角动量里德伯态,实现低频和直流电场测量,对应的场强为4.9 mV/cm.2022 年,杜艺杰等[25]基于里德伯原子天线实现了MHz—GHz 频段的电磁场测量.2023 年,Li 等[26]利用原子气室内部平行电极实现低频电场测量,频率为100 Hz 时的典型场强值为214.8 μV/cm,线性动态范围超过37 dB.

上述研究提供了低频电场的测量方法和测量技术,主要集中于电场频率测量和幅度测量.本文基于里德伯原子构建原子天线,通过气室内置电极技术实现室温原子气室的低频电磁场导入,利用原子天线技术将低频电场幅度测量转化为EIT 光谱的强度测量,开展低频电场的强度、频率、波形等参数测量.上述研究实验验证了原子天线的电磁场波形识别能力,为原子天线的低频电磁场参数测量提供了技术途径.

2 实验原理

图1(a)为铯原子6S1/2-6P3/2-65S1/2跃迁能级图,图1(b)为理论模拟得到的EIT 信号.能态 |1〉,|2〉,|3〉分别为铯原子基态6S1/2、中间态6P3/2和里德伯态65S1/2;γ3为里德伯态 |3〉的衰减率,γ2为中间激发态 |2〉到基态 |1〉的衰减率,γ1为基态 |1〉衰减率,γ1≪γ2(γ3).852 nm 探测光对应原子6S1/2—6P3/2跃迁,509 nm 耦合光对应原子6P3/2—65S1/2跃迁.

图1 (a)铯原子里德伯跃迁能级图;(b)理论模拟EIT 图Fig.1.(a) Rydberg transition energy level diagram of cesium atom;(b) EIT diagram of theoretical simulation.

旋波近似和偶极近似条件下,三能级原子系统哈密顿量矩阵形式表示为

其中,ℏ 为普朗克常数,Ωp为探测光的Rabi 频率,Ωc为耦合光的Rabi 频率,Δp为探测光的失谐量,Δc为耦合光的失谐量.原子密度矩阵ρ表示为

三能级原子系统中自发辐射的退相位矩阵L(ρ)表示如下:

相应的Lindblad 主方程表示如下[27,28]:

简化后阶梯型三能级系统的光学布洛赫方程表示如下[29]:

远失谐低频电场会导致里德伯原子的Stark频移,其会在三能级原子系统中引入双光子失谐并导致EIT 光谱的频移和强度变化[30].考虑合适的探测光和耦合光拉比频率,室温原子气室的EIT光谱响应带宽可达到MHz 以上,其允许实时响应kHz 频率的低频电场幅度变化.在弱电场条件下,EIT 透射强度与低频电场强度近似为线性关系,基于该效应可以实现低频电场的波形、幅度、频率等参数测量.图2 为EIT 信号强度随场强变化的数值模拟结果,可以看到,在特定参数范围EIT 信号强度与电场强度几乎是线性依赖关系.对不同波形电场信号导致的EIT 光谱线型进行了数值模拟,如图3 所示,弱场条件下,数值计算光谱线型与参考波形接近.

图2 EIT 信号强度随场强变化的数值模拟Fig.2.Numerical simulation of EIT signal strength variation with field strength.

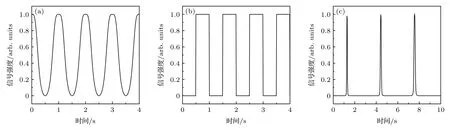
图3 数值模拟波形 (a)正弦波;(b)方波;(c) sinx/xFig.3.Numerical simulation waveform: (a) Sine wave;(b) square wave;(c) sinx/x.

3 实验装置

实验装置如图4 所示,852 nm 探测光共振耦合6S1/2(F=4)→6P3/2(F=5)态,激光器输出光束通过两组半波片和偏振分光棱镜(PBS)分成B1,B2,B3 三束;509 nm 激光耦合里德伯原子能级6P3/2→65S1/2态,激光器输出光束经半波片和偏振分光棱镜分成B4,B5 两束.光束B1 搭建饱和吸收光谱,利用铯原子D2 跃迁线6S1/2(F=4)→6P3/2(F=5)实现激光稳频;光束B2 与B4反向共线传输构建参考EIT 用于509 nm 激光稳频;光束B3 与B5 在带电极板的铯原子气室中反向共线传输形成EIT,用于构建里德伯原子天线开展低频电磁场波形测量.

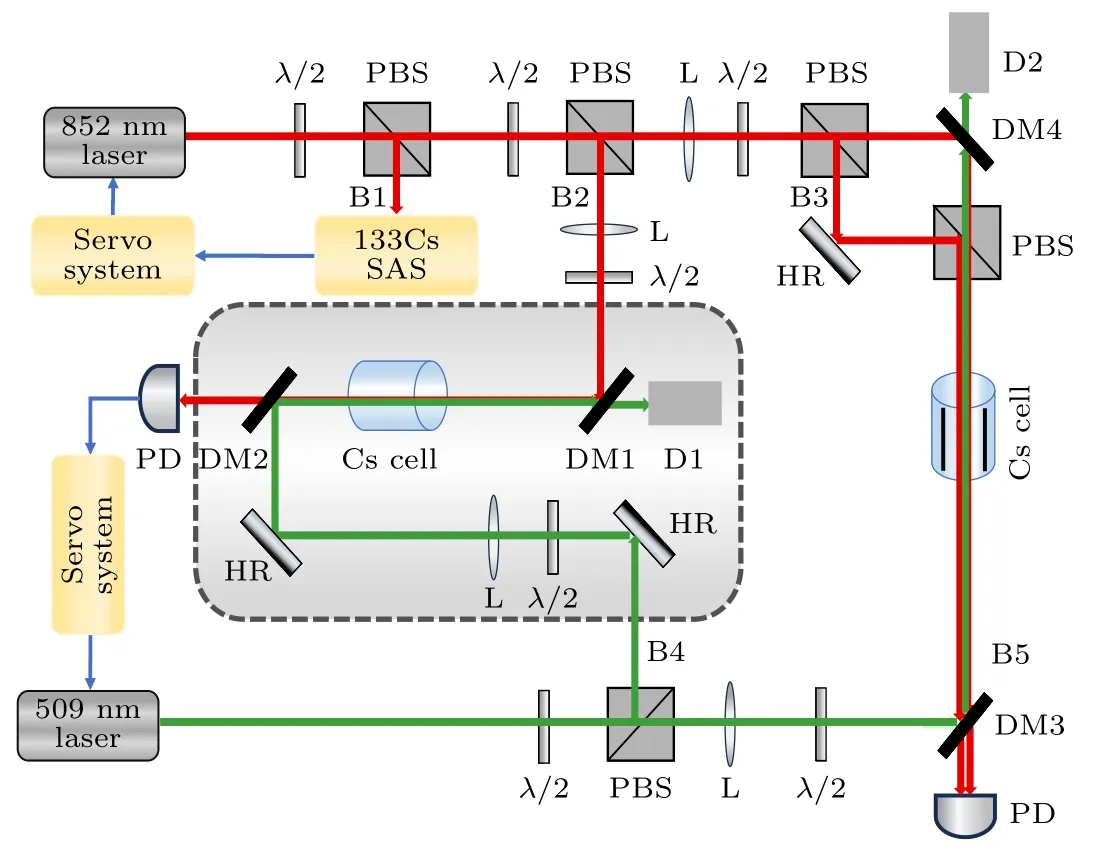
图4 铯原子光谱实验装置图,其中λ/2 为半波片,PBS 为偏振分光棱镜,L 为透镜,DM1 和DM4 分别为852 nm 高反射率(HR)和509 nm 高透射率(HT)双色镜,DM2 和DM3 分别为852 nm 高透射率(HT)和509 nm 高反射率(HR)双色镜,PD 为光电探测器,SAS 为饱和吸收光谱,D 为垃圾堆Fig.4.Experimental set-up.λ/2 represents half-wave plate,PBS represents polarizing beam splitter cube,L represents Lens,DM1 and DM4 represent 852 nm high reflectivity (HR) and 509 nm high transmissivity (HT) dichroic mirror,DM2 and DM3 represent 852 nm high transmissivity (HT) and 509 nm high reflectivity (HR) dichroic mirror,PD represent photodiode,SAS represents cesium atomic saturation absorption spectroscopy,D represents optical dump.

低频电场信号通过任意波形发生器产生,其一路输入示波器作为参考信号,另一路通过铯原子气室内置电极引入传感区域.实验中,852 nm 激光和509 nm 激光在电极板中心共线反向传输,穿过原子气室的852 nm 光束输入低噪声光电探测器,光电转换信号输入示波器进行数据采集和处理.

4 实验结果与分析

实验中利用参考光路中产生的EIT 光谱作为频率基准,将509 nm 耦合光频率锁定在6P3/2-65S1/2共振跃迁线上,获得稳定的EIT 强度信号.在此基础上,通过原子气室内置电极引入不同波形的低频电磁场,电场幅度变化会通过双光子失谐转化为EIT 透射信号强度变化,实验通过测量852 nm探测光强度变化,得到与低频电磁场相关的光谱信号.

图5(a)为1 kHz 正弦波的波形测量,图5(b)为10 kHz 正弦波的波形测量,黑色谱线为参考信号波形,红色谱线为里德伯原子天线的光谱信号.由图5 可知,参考信号(黑色)与测量信号(红色)吻合较好.实验测量了复杂电场波形的原子光谱信号.图6 显示了1 kHz 频率的低频电场波形测量,其中图6(a)为Gaussian,图6(b)为Lorentz,图6(c)为sinx/x,图6(d)为指数上升函数.基于自由空间原子气室研究电磁场波形测量,理论结果和实验测量具有很好的一致性.

图6 频率为1 kHz,高电平100 mV 低电平0 mV 时的参考波形和测量波形 (a)高斯函数;(b)洛伦兹函数;(c) sinx/x;(d)指数上升函数Fig.6.Reference waveform and measurement waveform at a frequency of 1 kHz,high-level 100 mV,low-level 0 mV: (a) Gaussian;(b) Lorentz;(c) sinx/x;(d) exponential rise.

图7 给出了10 kHz 频率的电场波形测量,高电平为100 mV,低电平为0 mV;其中,图7(a)为Gaussian 函数波形,图7(b)为Lorentz,图7(c)为sinx/x,图7(d)为指数上升函数.可以看出,在弱电场条件下,基于原子天线测量给出的电场波形与输入电场波形接近.通过频率测量,不同频率(图5—图7)的电场频率误差分别为0.6%,0.02%和0.13%,实验测量精度相对较好.通过计算参考波形与测量波形的相关性给出正弦函数和指数上升函数的相关性分别为0.986 和0.947.基于室温原子气室构建的原子天线响应带宽依赖EIT 光谱的响应带宽.EIT 的带宽可以通过探测光与耦合光拉比频率调谐,典型的EIT 带宽可以大于百MHz,高功率的探测光和耦合光可以增大EIT 响应带宽,但是相应的功率加宽效应会导致光谱展宽,其会影响原子天线的测量灵敏度.我们实验的探测光和耦合光拉比频率在1—10 MHz 范围可调,其给出的典型EIT 光谱典型响应带宽在MHz 左右,其满足kHz 频段的低频电场波形测量.

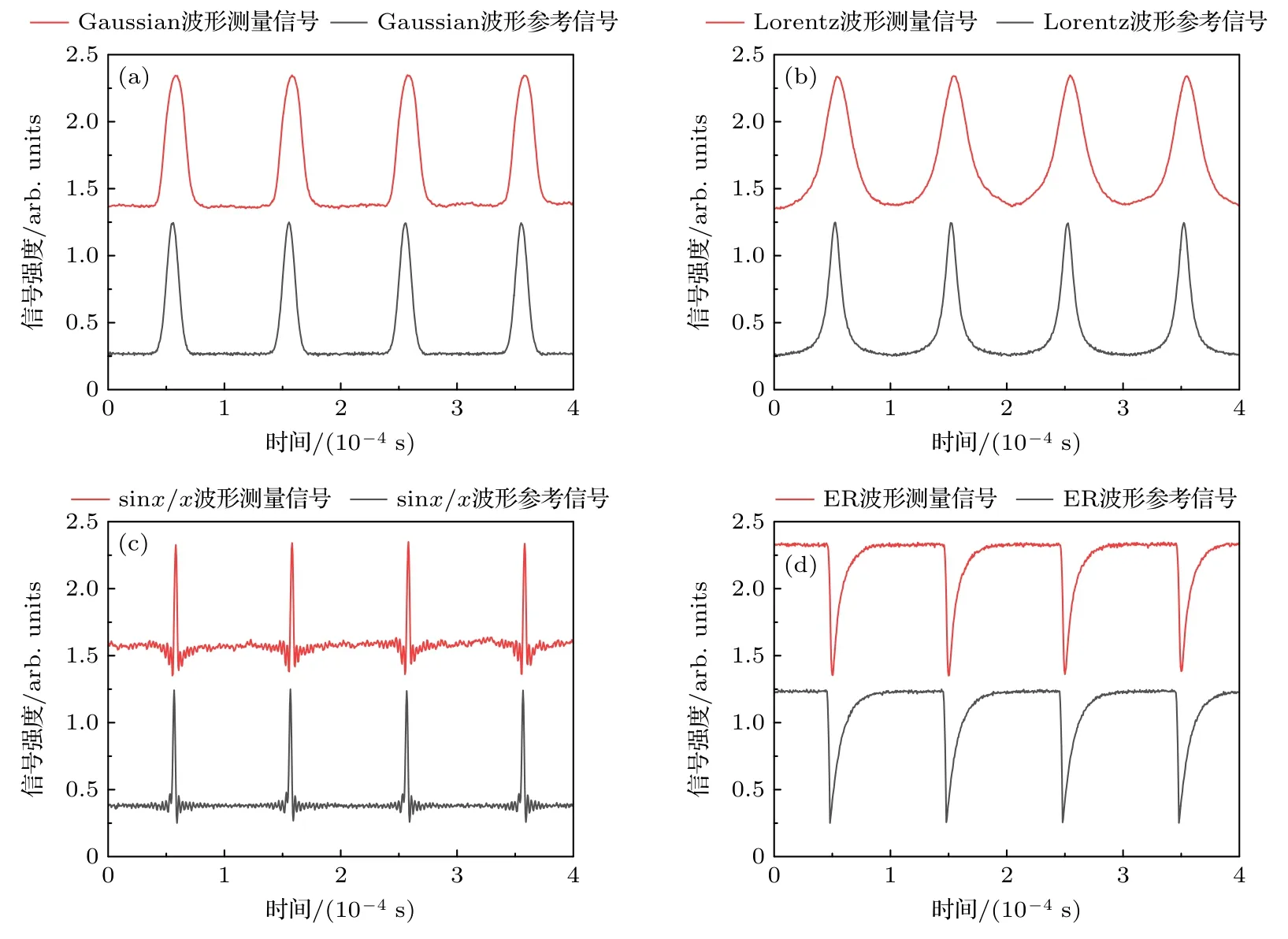
图7 多种波形测量,频率为10 kHz,高电平为100 mV,低电平为0 mV (a) 高斯函数;(b)洛伦兹函数;(c) sinx/x 函数;(d)指数上升函数Fig.7.Reference waveform and measurement waveform at a frequency of 10 kHz,high-level 100 mV,low-level 0 mV: (a) Gaussian;(b) Lorentz;(c) sinx/x;(d) exponential rise.

5 结论

本文基于室温原子气室构建原子天线,基于内置电极的里德伯原子开展kHz 频段电磁场测量.实验利用原子天线开展多种波形低频电场的频率测量,利用里德伯原子光谱对低频电场实现了波形重构.基于阶梯型三能级系统,数值模拟了低频弱电场条件下的EIT 光谱与电磁场波形关系,模拟结果与实验结果相符合.基于里德伯原子构建原子天线开展电磁场波形测量,其核心是场强测量带宽和测量灵敏度.测量带宽依赖光谱技术,通常的EIT 光谱或者光抽运光谱,可以通过增大泵浦激光功率将光谱响应带宽拓展到百MHz,其有利于突变信号的实时测量和重构.目前的原子天线技术,通过增大探测光和耦合光功率获得高带宽,其会导致测量灵敏度降低,该问题还有待探索.