正电子湮没符合多普勒展宽技术的材料学研究进展*

叶凤娇 张鹏 张红强 况鹏 于润升 王宝义 曹兴忠

(中国科学院高能物理研究所,多学科研究中心,北京 100049)

正电子湮没技术是研究材料微观结构的一种原子尺度表征方法,通过分析正电子湮没行为可以得到湮没位点处局域电子密度和原子结构信息.近年来,正电子湮没谱学技术已经发展成为优于常规手段的特色表征技术,其中符合多普勒展宽技术在研究缺陷附近的电子和原子结构方面具有独特优势,商谱曲线中高动量区域形状的变化反映了正电子湮没位点周围的元素信息.在常规符合多普勒展宽技术发展基础上,能量可调的慢正电子束流符合多普勒展宽技术在获取表面微观结构的深度分布信息上展示出独特的作用,同时也弥补了常规符合多普勒展宽技术只能表征体材料中缺陷环境的不足.本文结合国内外相关进展,综述了符合多普勒展宽技术在各类材料中的研究进展: 1)合金中空位型缺陷和纳米沉淀的演化行为;2) 半导体中晶格空位与杂质原子的相互作用;3)氧化物中氧空位和金属阳离子浓度的变化.除此之外,在聚合物中自由体积孔洞的大小、数量及分布的估算表征领域中,符合多普勒展宽技术也逐步得到应用.

1 引言

正电子湮没谱学(positron annihilation spectroscopy,PAS)是一种探测原子尺度缺陷以及微量元素含量变化的特色核分析技术,对测试样品无特殊要求、无损.该技术通过探测正电子与材料中电子湮没产生的γ射线所携带的信息来研究湮没位点附近微观结构信息[1-3].PAS 技术可用于表征合金、半导体、氧化物和聚合物材料等领域中开空间缺陷、电子密度和电子动量分布.目前广泛使用的PAS 测量方法包括正电子湮没寿命谱 (positron annihilation lifetime spectroscopy,PALS)、多普勒展宽谱(Doppler broadening spectroscopy,DBS)和符合多普勒展宽谱 (coincidence Doppler broadening spectroscopy,CDB)等[4,5].在探测与表征微观缺陷方面,PAS 已经发展成为了一门实用且成熟的技术,其中在多普勒展宽基础上发展起来的符合多普勒展宽能谱能够得到缺陷周围化学环境的信息,可为研究金属合金内部空位-溶质原子、溶质原子团簇结构的变化和类型提供有力的实验证据,CDB 技术也可以表征半导体中的氧空位、聚合物薄膜中的纳米孔洞等信息[6-9].此外,结合模拟计算可进一步确定空位团簇、空位-溶质原子和溶质原子团簇的尺寸以及类型.Ishizaki 等[10]利用CDB技术研究了Fe-Cu 合金在不同应变速率下空位团簇和Cu 偏析物的尺寸及其浓度变化.Elsayed 等[11]用蒸发法在GaAs 样品上沉积Cu 层,并通过CDB技术表征出沉积并未导致样品中形成Cu-空位-溶质原子复合物,且空位是一种本征缺陷.Xia 等[12]利用CDB 技术研究了离子交联壳聚糖膜的亚纳米级分子堆积,确定了C 原子和H 原子易富集在离子交联中自由体积纳米孔洞的周围.常规CDB 技术使用放射源发出的正电子,能量不可变,主要用于探测样品中整体的缺陷特征.在此基础上发展起来的慢正电子束流CDB 技术通过改变正电子的入射能量(在30 keV 的正电子能量变化范围内)可以得到特定深度内的缺陷分布信息,一般用来研究材料近表面到亚微米范围内、多层薄膜中的微观缺陷和结构的分布等信息,该技术已经成为一种精确测量原子尺度缺陷和元素偏析等信息的新兴无损核技术[13-16].

综上所述,CDB 技术对金属、薄膜材料等的微观结构与缺陷,尤其是金属中的第二相纳米粒子具有高灵敏探测能力,在开空间缺陷和第二相表征方面表现出了优越性.本文首先对CDB 技术的原理作出介绍,并对常规CDB 技术和慢正电子束流CDB 技术在各类材料中的应用进行分类,分别综述CDB 技术在材料中微观缺陷和元素偏析等方面的研究进展.

2 符合多普勒技术

2.1 正电子湮没的多普勒展宽效应

多普勒展宽能谱技术是除了PALS 技术之外较为广泛应用的表征方法,主要通过测量正负电子湮没之后辐射的γ光子的能谱来表征材料中的微观缺陷信息.动量分别为零的电子和正电子发生湮没后,由于系统总能量守恒,两个能量为511 keV的γ光子会呈现180°相反方向运动.但是,参与湮没的电子和正电子一般有初始动量,会产生多普勒效应,这导致产生的γ光子动量和不为零且运动方向有一定的倾斜角,结果如图1 所示.由于正电子-电子湮没对运动也会导致湮没辐射的多普勒增宽,既湮没辐射的γ光子能量为E=m0c2±ΔE[17],由于频移Δv/v=vL/c,则多普勒能移为

图1 正电子湮没中的多普勒展宽原理Fig.1.Doppler broadening principle in positron annihilation.

其中,c为光速,νL和PL分别代表湮没对在观测方向(纵向方向)上的速度分量和湮没对的横向动量.由此产生的两个光子的能移大小相等,符号相反.若湮没时电子的能量为4 eV,则正负电子湮没对速度v与光速c的比值约为2×10-3,(1)式可转化为

因此,最大的多普勒展宽值为2|ΔE|≈2 keV,即湮没γ射线能量展宽仅为2 keV.对于相同样品,ΔE随其他变量的变化就更小了,但为了观察多普勒展宽的细微改变,可减小每道的能量宽.由于湮没事件的积累,湮没光子按能量的分布是一个以511 keV 为中心的对称分布,该能量峰的形状与材料的特征信息密切相关.

但由于DBS 测量系统只含有一个高纯Ge 探测器,测量结果会出现信号堆积、探测器的电荷吸收、1.28 和0.511 MeV 康普顿散射等现象.这都会导致谱线本底增加,DBS 谱中峰值与高能端本底之比达到200∶1,使得高动量电子湮没的翼区信息很难从本底中分离出来.高动量电子湮没信息主要反映材料缺陷附近的微观结构,但由于DBS 存在高动量区计数问题,得到的主要是低动量部分的信息,而难以对核芯电子的高动量分布进行研究.

2.2 CDB 技术的测量方法和原理

符合多普勒展宽能谱是在多普勒展宽基础上发展而来的,是一种新型且可以用于元素鉴别的正电子谱学技术.CDB 测量技术是对同时探测到的两个γ光子进行时间和能量符合,从而消除本底的影响,将高动量电子的湮没信息分离出来.CDB 技术相比DBS 技术具有峰谷比大、能量分辨好的特点[18-20],因此在表征高动量区核芯电子的信息方面有明显优势.

图2 是双探头CDB 测量系统的示意图.两个高纯Ge 探测器构成符合多谱勒展宽系统,检测到2 个能量为E1和E2的湮没γ光子:

图2 CDB 测量系统示意图Fig.2.Schematic diagram of CDB measurement system.

其中,m0为电子的静止质量;Eb为正电子和电子的结合能;PL为湮没电子-正电子的纵向动量;c表示光速.两个γ光子的能量分别表示为E1和E2,则能量和为ET=E1+E2.根据能量守恒,湮没正负电子对的总能量为ET=2m0c2-Eb.由于大多数正电子在材料中会先经历热化而后参与湮没,Eb可以忽略.除此之外,两个湮没光子的能量差(ΔE=E2-E1)可近似表示为ΔE≈cPL,其中,PL代表电子和正电子的动量.因此,通过同时测量两个湮没γ光子的能量,并通过E2-E1来重建多普勒展宽谱,即电子的动量分布[21].

图3(a)和图3(b)为纯Fe 和简单二元合金Fe-Cu 样品的二维CDB 谱图,横纵坐标分别代表两个γ光子的能量差与能量和.图3(c)为选取图3(a)和图3(b)中E1+E2=(1022±2) keV 附近的计数重新构建的纯Fe 和Fe-Cu 样品CDB 谱图,纵坐标为归一化计数,横坐标为电子动量.图3(c)插图为Cu 特征峰(PL=12×10-3m0c—28×10-3m0c)附近的扩展图,由图可知Fe-Cu 合金曲线的幅值高于纯Fe,说明该样品中的正电子与Cu 的3d 电子湮没会导致曲线升高.图4 为纯Fe 的CDB 谱与DBS 对比图,可知经过双探头符合后,CDB 中的有效计数比例大大提高,且本底降低.

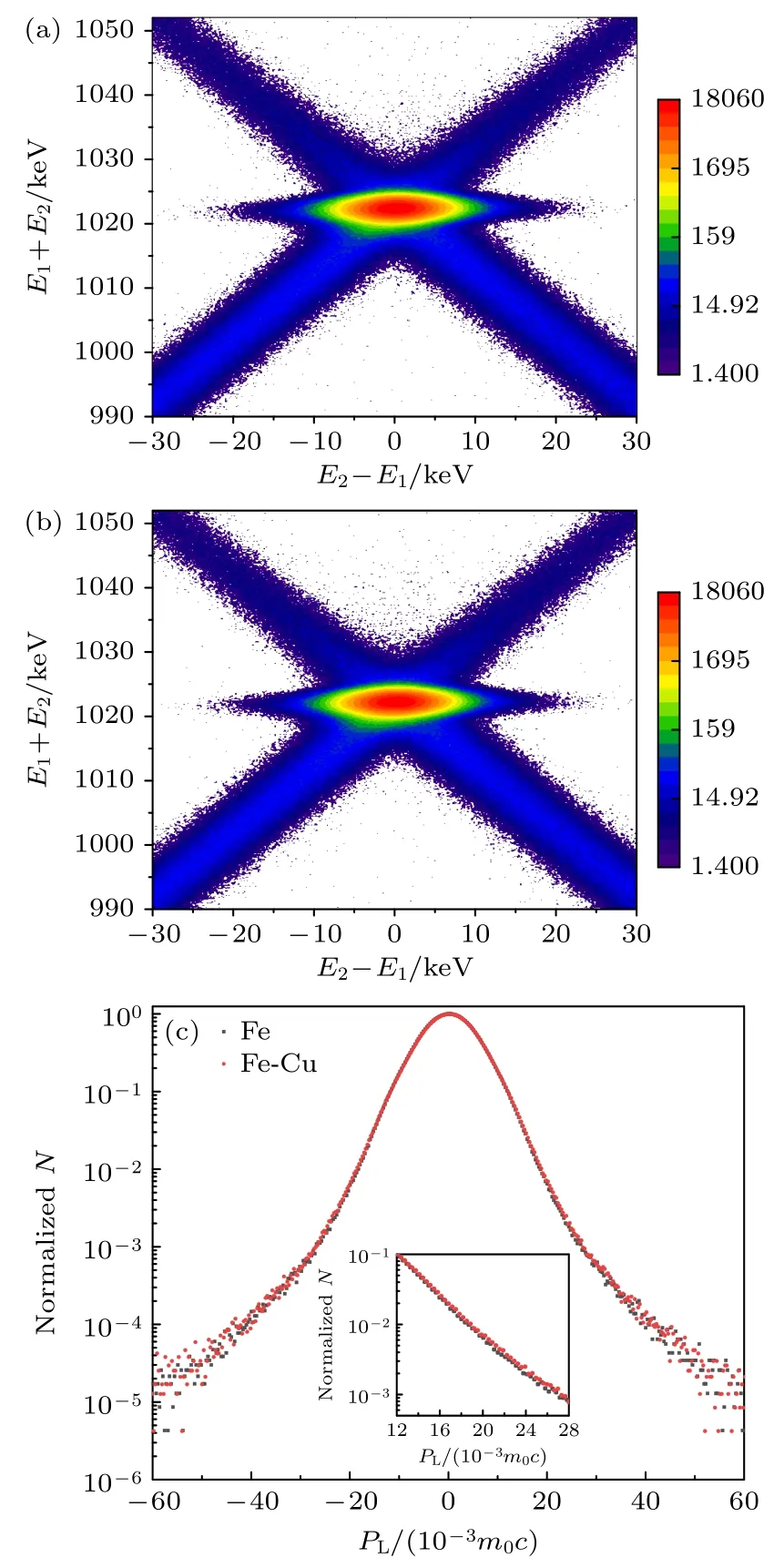
图3 不同样品的CDB 谱图 (a) 纯Fe 样品;(b) Fe-Cu样品;(c)对角化后的纯Fe 和Fe-Cu 样品.插图为Cu 特征峰(PL=12×10-3m0c—28×10-3m0c)附近的扩展图Fig.3.CDB spectra of different samples: (a) Pure Fe;(b) Fe-Cu samples;(c) pure Fe and Fe-Cu samples after diagonalization.Inset is an extended view near the Cu characteristic peak (PL=12×10-3m0c—28×10-3m0c).

如图5(a)所示,CDB 谱中的动量分布可以主要分为两个区域: 一个是靠近峰值位置(PL＜)的低动量区域,即S参数,主要反映低动量电子的湮没信息,即空位型缺陷的信息;另一个是高动量区域＜PL,即W参数,主要反映湮没位点附近的化学环境信息,如缺陷周围的溶质原子等.为了便于分析高动量电子的信息,通常对CDB 曲线采用商谱法处理: 将待分析样品的湮没能谱与标准样品的湮没能谱各道分别对齐,然后各道计数分别相除后得到商谱.通过比较不同样品的商谱形状,如峰值与峰的位置,可以研究湮没位置处带有元素信息的高动量电子信息变化.高动量电子是指原子的内层电子,由于每个元素511 keV 湮没线的形状都有所不同,当被俘获正电子的波函数与缺陷周围的原子重叠时,通过分析湮没谱图的高动量区域就可以识别原子类型[22].图5(b)是Fe-Cu 合金中的CDB 商谱图.由于Cu 原子的正电子亲合势较强,当Fe-Cu 合金中出现Cu 原子聚集时,此处的正电子密度会增大,正电子主要与其3d 电子(高动量电子)湮没,这主要反映在图5(a)的B 区.当材料中存在空位型缺陷时,正电子与空位附近的电子湮没,这主要反映在图5(a)中的A 区.

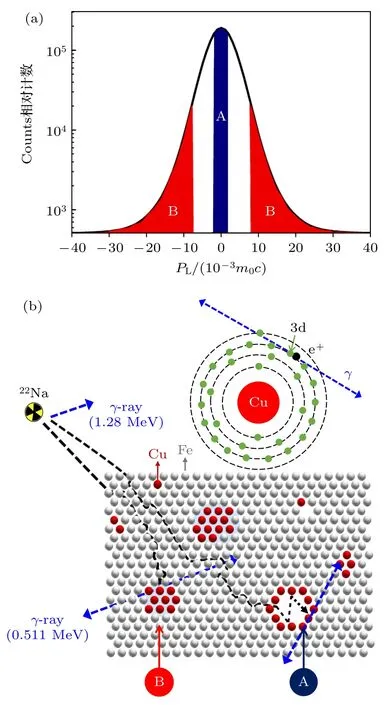
图5 (a) 纯Fe 的CDB 中S 参数及W 参数的定义区域;(b) Fe-Cu 合金中的正电子湮没Fig.5.(a) Definition area of S parameter and W parameter in CDB of pure Fe;(b) schematic diagram of positron annihilation in Fe-Cu alloy.

Asoka-Kumar 等[23]首次将Al 做参考,测量并计算了几种典型元素的CDB 谱图,结果如图6(a)和图6(b)所示.元素周期表中相邻元素的电子结构相似,如Al 和Si,不相邻元素之间的差异则非常显著.随后,Brusa 等[24]和Xi 等[25]较为系统地补充了27 种纯元素的CDB 谱图,概述了各元素峰的位置和振幅的规律,并讨论了正电子和各元素中轨道电子的湮没情况对高动量区峰位的影响.后续研究者可以上述工作为参照,根据实验样品CDB 曲线的峰值和峰位表征正电子和高动量电子的湮没特征,获取空位型缺陷、溶质原子团簇、空位-溶质原子复合物的信息.

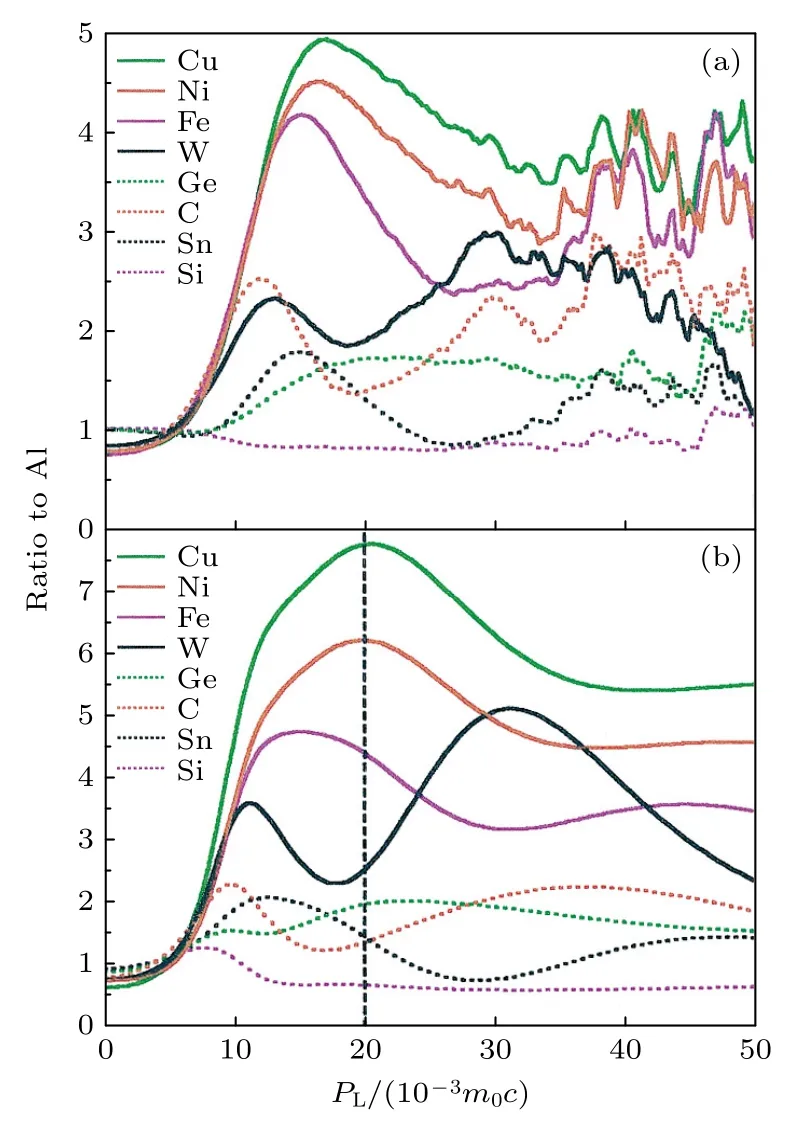
图6 典型元素与Al 的商谱图[23] (a)实验数据;(b)理论数据Fig.6.Spectra for different elements after normalizing to Al[23]: (a) Experimental curves;(b) theoretical curves.

在实际测试中,由于亲合势的不同,正电子会优先选择性地与某种元素的电子湮没.图7 为不同的金属元素与正电子的亲合势[9],其中Ni 的亲合势为-4.46 eV,即在同等条件下,Ni 元素更容易与正电子结合(能量最低原理).此外,正电子与高动量电子中各轨道电子的湮没概率也不同.郗传英[9]计算了纯金属各轨道电子和正电子的湮没比例,在同一周期元素中,湮没概率主要与元素的最外层和次外层电子有关,若最外层电子是与低动量区有关的s 或p 电子时,正电子与d 电子的湮没信息主要反映在高动量区,且特征峰的形状与d 电子的个数有关[1,26].高动量处的峰值主要受到两个因素的影响: 1)正电子与芯电子湮没或正电子在杂质-空位复合物中的湮没;2)正电子在空位或空位团簇中湮没.当正电子在空位型缺陷中湮没时,与元素中高动量电子的湮没概率会降低,这会导致CDB 高动量区的峰值降低[27,28].以纯Al 作参考的纯元素CDB 谱图以及正电子与纯元素的亲合势研究结果为表征二元合金和多主元合金等材料中缺陷和元素偏析奠定了基础.

图7 各种金属元素的正电子亲合势A+ (单位: eV)[9]Fig.7.Positron affinity A+ (unit: eV) of metal elements[9].

为了更详细地反映样品中各类信息的变化,将实验样品与不同的参考系作商谱,CDB 曲线高动量区的特征峰形状就会不同.

例如,Jin 等[29]将辐照前后的Fe-Cu 合金分别与纯Fe 和纯Cu 元素做商谱图,从图8 和图9可知,辐照后的Fe-Cu 样品均在PL=25×10-3m0c处显示出与纯Cu 相似的特征峰,表明正电子被与Cu 原子结合的类空位缺陷所捕获或被捕获在Cu 析出物中.可近似理解为排除了正电子与Fe 的3d 电子湮没的影响,主要反映与Cu 原子相关的缺陷信息.同理,Fe-Cu 样品与纯Cu 做商谱时,主要表征与Fe 原子相关的缺陷信息变化.从图9 可知,辐照前后的Fe-Cu 合金在PL=25×10-3m0c附近的曲线趋势较为平坦,这表明辐照后正电子几乎不与Fe 中的电子湮没[29].Zhong 等[30]将不同退火温度下的FeCrMnCuMo 合金与不同的参考系作商谱,CDB 结果如图10 所示,不同参考系下退火样品以及各元素的CDB 曲线形状不同.与纯Fe 作商谱,773 K 温度下退火样品的CDB 谱表现为特征峰,且与纯Cu 的曲线一致,这表明合金在该温度下出现了Cu 偏析;随着退火温度的继续升高,峰值逐渐降低,表明Cu 偏析尺寸或密度降低.与as-cast FeCrMnCuMo 作商谱,当退火温度为773 K 时,PL=22×10-3m0c处出现了一个与纯Cu 特征曲线相似的平台.退火温度达到1073 K时,CDB 比值曲线在高动量区呈现出一个谷.由此可以发现,选择不同的参照样品作商谱对CDB 图谱的影响较大,但反应结论相一致.对于其他实验结果,若将相同样品选择不同的参照系样品作商谱,也可采用以上方法更全面地反映材料中开空间缺陷信息和元素信息.

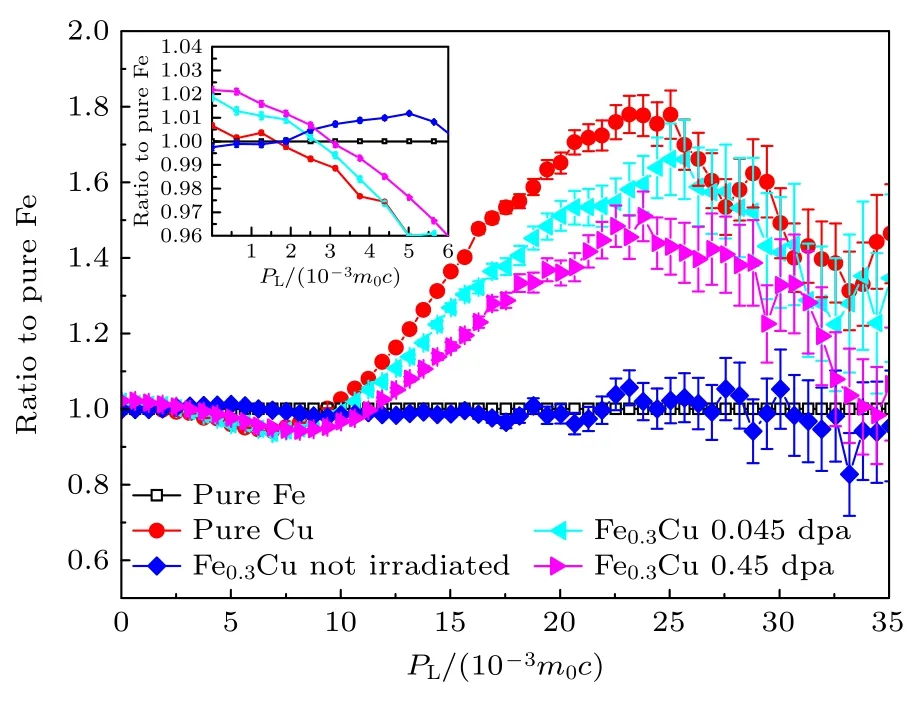
图8 纯 Cu,Fe-0.3%Cu 合金在不同剂量下辐照后与纯Fe 的CDB 谱[29]Fig.8.CDB spectra with pure Fe of pure Cu,Fe-0.3%Cu alloy irradiated at different doses[29].

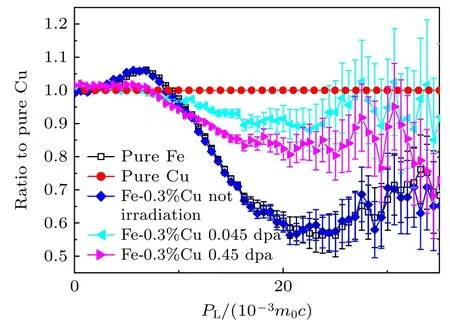
图9 纯 Cu 和Fe-0.3%Cu 合金在不同剂量下辐照后与纯Cu 的CDB 谱[29]Fig.9.CDB spectra of pure Cu and Fe-0.3%Cu alloy irradiated with pure Cu at different doses[29].

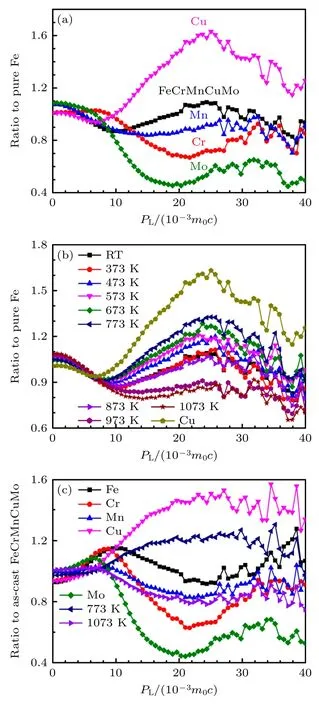
图10 (a) FeCrMnCuMo 合金、纯Cr,Mn,Cu 和Mo 相对于纯Fe 的CDB 谱图[30];(b) 铸态、退火态FeCrMnCuMo合金和纯Cu 相对于纯Fe 的CDB 谱图[30];(c)纯Fe,Cr,Mn,Cu 与FeCrMnCuMo 在773 K 和1073 K 下退火相比于铸态FeCrMnCuMo 合金的CDB 谱图[30]Fig.10.(a) CDB ratio curves of the FeCrMnCuMo alloy,pure Cr,Mn,Cu and Mo with respect to pure Fe;(b) ascast,annealed FeCrMnCuMo alloy and pure Cu with respect to pure Fe;(c) pure Fe,Cr,Mn,Cu and Mo and annealed FeCrMnCuMo alloy at 773 K and 1073 K with respect to the as-cast FeCrMnCuMo[30].

2.3 基于慢正电子束流的符合多普勒展宽技术

前面所述的正电子测试方法是利用放射源(22Na,64Cu,58Co 等)发射正电子,其所携带能量在0—545 keV 范围内连续分布,只能探测块状材料整体的缺陷信息,在研究样品的表面缺陷和结构时存在一定的限制.因此需要一种能量可调的正电子束,以获得纳米深度范围内缺陷分布信息.Cherry[31]首次观察到了经过慢化的正电子束流,之后Canter 建立了第一台慢正电子束流装置,并用于材料的表面态等性质的研究.经加速器或者放射源中产生的高能、能量连续的正电子经历过慢化后,再加速至特定能量并利用电磁聚焦得到单一能量的慢正电子束流,其能量可控制在0 至几十keV范围内.慢正电子束流技术显著的优点在于正电子能量分布较窄和能量连续可调,具备表征材料中不同深度信息的能力.慢正电子的探测深度由入射的能量定义:

其中,Z(E)为正电子入射深度(nm);E为慢正电子的入射能量 (keV);ρ为材料密度,单位为kg/m3.慢正电子束流CDB 技术通过改变入射正电子的能量可表征材料表面到亚微米之间特定深度的微观结构信息,弥补了常规CDB 技术只能表征体效应的不足.

3 常规CDB 谱在材料领域研究中的应用

3.1 常规CDB 谱在金属/合金研究中的应用

正电子湮没谱学技术在金属/合金领域的研究最早,且应用领域最广.已有研究者对金属/合金在经过淬火、塑性形变、热处理方式等产生的空位、空位团簇、气体-空位复合体、位错、晶界等开空间缺陷进行了表征,随后又聚焦于合金在辐照、相变和氢脆方面的问题,并取得了大量研究成果.特别是,常规CDB 技术在金属合金材料表征方面的应用也越来越多.利用CDB 技术对高动量电子的信息异常敏感的特点,可对合金材料中缺陷附近的元素信息进行甄别,如杂质原子、元素偏析以及杂质-空位复合体.

金属在经过塑性变形后会产生位错、空位和空位团簇,这些缺陷可以为第二相粒子提供形核位点和通道,有助于形成第二相析出物.在Fe-Cu 合金体系中,Cu 析出相是正电子的理想俘获点,每个正电子的波函数在空间上完全局限于细小的析出相中,而析出相是一种类似量子点的正电子态.Onitsuka 等[32]形变了Fe-1.0% (质量含量为1.0%,后文不再赘述) Cu 合金后并在50—500 ℃之间进行等时退火,采用常规CDB 技术研究了Cu 偏析行为和Cu-空位复合物的演化.如图11 所示,经室温淬火和形变后合金的CDB 曲线在高动量区显示出Cu 特征峰,这表明淬火和形变后形成了Cu 空位复合物.高温退火促进了Cu 空位团簇的解离,最终形成了与基体共格的Cu 析出相.Bartha 等[33]对Ti-6%Al-7%Nb 合金进行形变处理后,采用常规CDB 技术研究了形变对合金中晶格缺陷及超细晶组织热稳定性的影响,结果显示随着退火温度的升高空位型缺陷逐渐回复.

图11 Fe-1.0%Cu 合金在不同温度下等时退火的CDB 谱图[32]Fig.11.CDB spectra of isochronous annealing of Fe-1.0%Cu alloy at different temperatures[32].

合金在经过固溶和形变等处理后在较高温度下放置的过程称为时效处理,时效后形成的团簇是正电子的有效捕获陷阱.Nagai 等[34]对Fe-1.0%Cu 样品进行不同时间的时效处理,采用常规CDB技术揭示了纳米Cu 粒子的结构特征.如图12 和图13 所示,随时效时间的增加,CDB 谱中Cu 特征峰(PL=24×10-3m0c)的幅值降低,说明高温促进了Cu 析出相的密度或尺寸降低.本课题组[35]采用CDB 技术研究了不同温度下Al-Ag 合金中的Ag 团簇以及单空位特征变化.研究结果显示,高温会促进Ag-空位复合物分解为Ag 团簇和单空位,同时CDB 曲线的高动量区幅值逐渐降低.该研究也证实了低温下CDB 技术是研究合金早期时效阶段缺陷和析出相组织演化的重要方法.

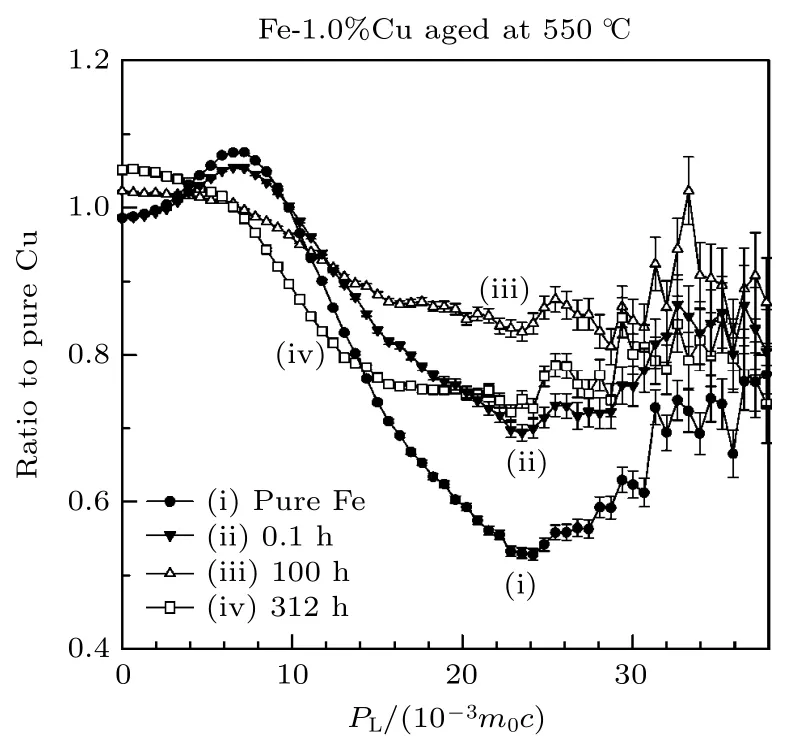
图13 (a)纯Fe,Fe-1.0%Cu 合金在不同时间时效后的CDB 谱图[34]Fig.13.CDB spectra of pure Fe,Fe-1.0%Cu alloy aged at different times[34].

近年来,作为一种金属材料研究领域的“超级新星”,多主元合金由于其独特的物理性质而在金属材料的各个应用领域得到了广泛研究.多主元合金中的元素有相似的原子百分比,元素位置分布的随机性和原子半径的不同,这使得多主元合金的微观结构更加复杂,缺陷的识别也更加困难.利用CDB 技术对高动量电子分布信息的灵敏特性可进一步表征常规测试手段无法测试的信息,如溶质原子团簇信息,空位型缺陷等.Abhaya 等[36]也采用常规CDB 技术测量了FeCrCoNi 多主元合金在从室温到1273 K 的等时退火处理中微观结构的变化.研究结果显示在PL=(10—15)×10-3m0c观察到一个位错相关峰,且特征峰值随着温度的升高而升高.为了进一步确定空位型缺陷的性质,结合理论模拟计算了含空位缺陷的不同种FeCrCoNi 合金与含单空位的纯Fe 的CDB 曲线,发现含单空位的FeCrCoNi 合金与含有单空位Fe 的比值曲线相似,这表明FeCrCoNi 中的缺陷是由于淬火过程产生了单空位,并与位错结合.Ye 等[37]对塑性形变之后样品进行等时退火处理,通过常规CDB 技术研究了FeCrCoNiMn 合金中Cr 偏析和空位的演化,结果显示高温会促进空位的迁移和聚集,而空位迁移是异质结构Cr 偏析物演变的驱动力.2019 年,Zhong 等[30]对FeCrMnCuMo 多主元合金进行等时退火实验,并采用常规CDB 技术研究了其微观结构的热稳定性.研究结果显示,退火温度大于473 K 时会产生Cu 偏析,Cu 特征峰的峰值在473—773 K 之间随温度逐渐升高,这表明Cu 偏析尺寸逐渐增大.但Cu 特征峰的峰值在973 K 时明显降低,这是由于Cu 偏析物密度降低或尺寸减小.

由于中子辐照在材料中的穿透性高,它能够引发合金材料整体的开空间缺陷演变和元素偏析行为,这对CDB 谱中高动量区和低动量区的曲线特征影响较大.Nagai 等[38]采用快中子辐照了Fe-Cu 合金,随后进行常规CDB 谱测试,结果如图14所示.低动量区(小于3.5×10-3m0c)的商谱曲线比值大于1,表明辐照引起入了微孔洞、空位和位错环,PL=25×10-3m0c附近的宽峰表明辐照诱导了合金中出现Cu 析出,且随着Cu 含量的增加,Cu 析出相的尺寸或密度增大.此外,他们还发现Cu 析出物的回复温度与合金中Cu 含量有关.Xu[39]等也采用CDB 技术研究了中子辐照Fe-Cu 合金后随温度退火过程中Cu 偏析行为并提出了Cu 析出物的两种形成机制: 空位迁移导致的析出和Cu 原子在微孔洞中的聚集.

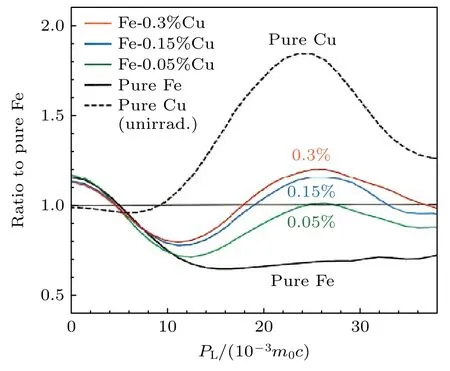
图14 快中子辐照后的Fe-0.3%Cu,Fe-0.15%Cu,Fe-0.05%Cu,纯Fe 和纯Cu 的CDB 谱图[38]Fig.14.CDB spectra of pure Fe,pure Cu,Fe-0.3%Cu,Fe-0.15%Cu,Fe-0.05%Cu after fast neutron [38].

氢进入材料中会产生空位、氢空位复合体甚至是氢化物,这些缺陷与合金的氢脆性能密切相关,近年来,常规CDB 技术也逐渐应用于氢引入导致的微观缺陷的表征.例如,Wang 等[40]通过常规CDB 技术测量了5 xxx 铝合金在高压充氢后微观缺陷的变化,结果如图15 和图16 所示,充氢导致低动量区的比值异常降低,可能是金属杂质抑制了空位形成.由于Mg 原子对H 的强亲和力会导致H会优先填充Mg 原子周围的空位并形成了Mg—H键,因而正电子与Al 的2p 电子的湮没概率增加会导致高动量区出现Al 的特征峰.

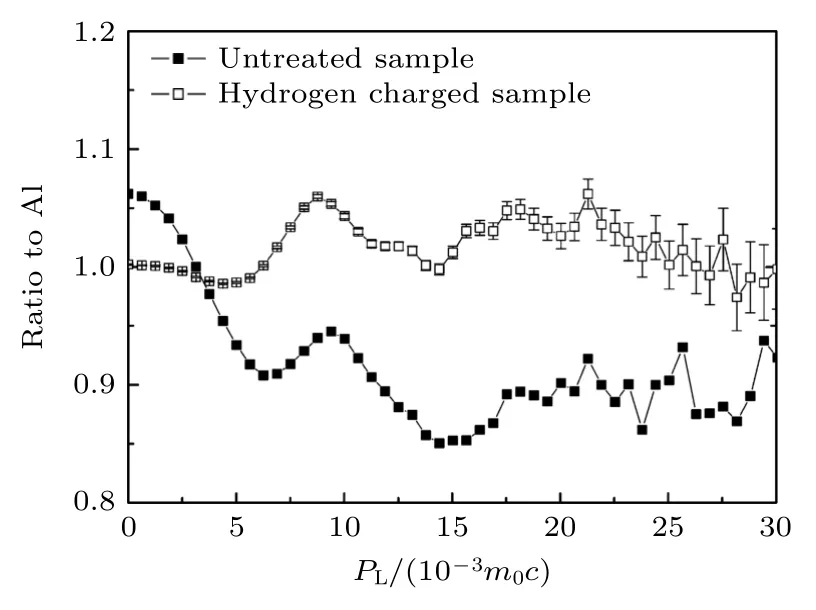
图15 未充氢和充氢样品的CDB 谱图[40]Fig.15.CDB spectra of uncharged and hydrogen-charged samples[40].

图16 充氢样品和退火后纯Al 的CDB 谱图[40]Fig.16.CDB spectra of hydrogen-charged samples and annealed pure[40].

王茜茜[41]对Ti 和Ti-Mo 合金进行电化学充氢,采用常规CDB 技术在纯Ti 的PL=3.5×10-3m0c处测到了氢化钛相关峰,且峰值随着充氢含量的增加而增加.如图17 所示,由于Mo 的加入诱发了氢化物附近电子态密度变化,这会导致氢化物特征峰向右移动,并在高动量区形成两个氢化物特征峰.

图17 纯 Ti (a)和Ti-Mo 合金(b)充氢前后的CDB 曲线[41]Fig.17.CDB curves of pure Ti (a) and Ti-Mo alloy (b) before and after hydrogen charging[41].

常规CDB 技术在研究高能量的离子和质子辐照以及退火后引起的气体原子和空位复合物的演化规律方面也较为广泛.Sabelová 等[42]用常规CDB 技术表征了Eurofer 97 合金在辐照后,He 空位复合体随退火温度的热演化.研究显示,退火温度升高会导致氦向空位团簇扩散,此时高动量区He 特征峰值升高,这说明He 原子占据了辐照产生的空位型缺陷.随后他们将实验和理论计算相结合证实了在不同温度下的He-空位复合物中存在He 原子的饱和值.Fujii 等[43]利用常规CDB 研究了A533B 合金在电子辐照后Cu 原子的聚集行为.结果显示当电子辐照剂量超过1 dpa 时Cu 原子发生聚集;高温辐照时样品CDB 曲线的高动量区峰值随剂量的增加而降低,这表明Cu 偏析物尺寸逐渐减小而空位型缺陷逐渐增多.

3.2 常规CDB 技术在氧化物材料中的应用

在氧化物掺杂体系中,由于替代离子的电荷补偿效应会产生氧空位,而氧空位的特征与材料的物理化学特性密切相关.利用空位对正电子的捕获作用可以获取有关空位尺寸和浓度的信息以及体系的物理特性.

Ge 等[44]采用CDB 技术测量了不同含量La掺杂Bi1-xLaxFeO3的缺陷特征,如图18 所示.所有样品均在11×10-3m0c处测到了与氧的2p 电子湮没相关峰,但特征峰的形状不同,研究认为这是由于La 含量的变化导致了缺陷附近原子结构发生变化.Kundu 等[45]制备了氧化物纳米复合材料xAg2O-(1-x)(0.3CdO-0.7MoO3),通过CDB 技术研究了不同Ag2O 掺杂量下开空间缺陷和氧离子浓度的变化,并且结合PALS 结果确定了Ag2O 基体中存在较高浓度的氧空位.Qin 等[46]表征了具有大介电常数的Sr1-xLaxTiO3(SLTO)陶瓷中的点缺陷特征,CDB 结果显示出Ti 空位是STO 陶瓷的主要缺陷,而当La3+离子掺杂替代 Sr2+离子时会产生Sr 空位和缺陷偶极子结构,同时结合PALS 结果也验证了空位补偿机制在SLTO 陶瓷中占主导地位.Ahmed 等[47]分析了不同温度下制备的氧化镉纳米晶体内部的缺陷,CDB 结果显示材料中存在Cd2+单空位和Cd2+-O2-空位缺陷,结合光学性能测试可知,缺陷和与缺陷相关的演化过程以及特性可以作为宽带隙半导体技术应用的可用性指标.Thorat 等[48]通过采用不同铕(Eu)含量掺杂氧化铈(CeO2),并采用CDB 技术表征出在Eu 浓度的合适范围内Ce 离子会被还原,并释放出氧空位,且掺杂浓度越高,空位聚集越多.Das 等[49]采用溶胶凝胶法制备了MgO 纳米晶体并在不同条件下退火得到不同尺寸的样品,CDB结果显示由于退火温度的升高纳米晶体中的空位型缺陷聚集形成了空位团簇,同时高温也促进了纳米晶体的生长.此外,CDB 谱也证明了除Mg2+单空位可捕获正电子之外,正电子还可以被捕获在中性空位和带负电的三空位中,这与正电子湮没寿命结果的相一致.Ghosh 等[50]采用PALS 和CDB技术研究了二氧化钛(TiO2)纳米粒子在氧气和氩气的高温退火过程中,由锐钛矿结构向金红石结构转变过程中空位型晶体缺陷的演变,CDB 结果显示曲线特征峰的位置并没有因为退火而改变,这表明正电子捕获点周围的元素分布保持不变.但在O2和Ar 不同气氛中退火的样品之间,其缺陷特征存在明确的差异.Das[51]采用烧结法制备了SiO2纳米颗粒,并通过CDB 技术研究发现烧结引起自由体积孔洞的半径发生收缩现象,在烧结温度为1200 ℃时,CDB 比值曲线峰高的降低表明缺陷随着退火温度的升高而消除.此外,研究者从CDB曲线中提取的S参数和W参数表明样品中不存在位错线和位错环.

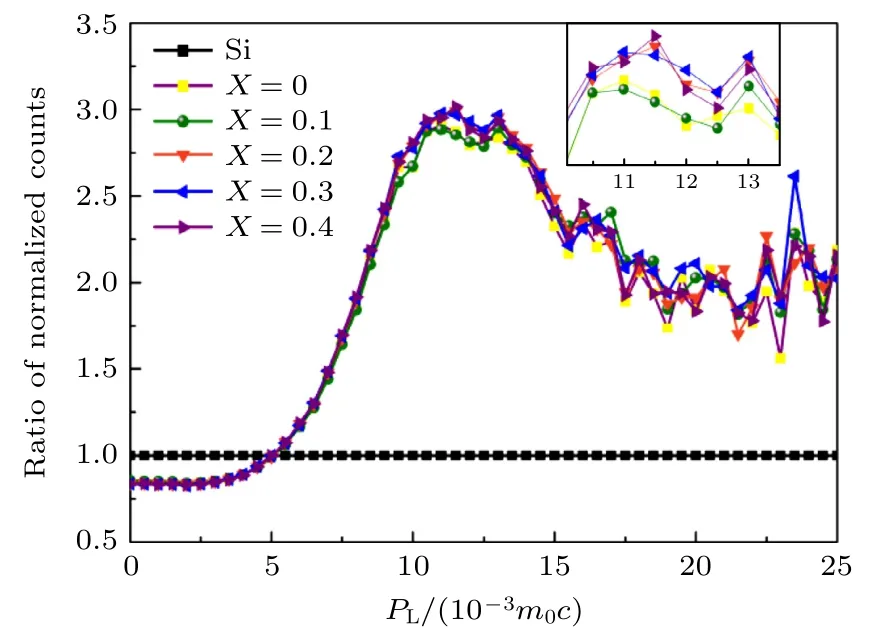
图18 不同浓度La 掺杂Bi1-xLaxFeO3 的CDB 谱图[44]Fig.18.CDB spectra of Bi1-xLaxFeO3 samples doped with different concentrations of La[44].

3.3 常规CDB 技术在半导体材料中的应用

空位等点缺陷可以降低自由载流子的密度或介导,它在决定半导体材料的关键性能方面起着重要作用,认识缺陷的形成、演化及量化缺陷对研究半导体材料的物理性质具有重要意义.常规CDB技术是表征半导体中中性和带负电荷的开空间缺陷、空位周围的元素信息和晶格空位与杂质原子相互作用的重要工具.

离子注入是半导体材料制备和改性的重要方法,它能实现将特定的离子注入到材料表面,达到调控半导体材料电学性能和化学特性的目的.同时,离子注入也能够导致材料产生晶格畸变、开空间缺陷,而这类微观结构的演化与物理性能密切相关.Yu 等[52]对p 型4H-SiC 半导体进行Ge+离子注入后经过等时退火处理,随后利用常规CDB检测了离子注入后微观结构的变化.结果如图19所示,离子注入后产生的空位型缺陷引起CDB 曲线的低动量区升高,并且在退火后样品中未观察到明显的Ge 特征峰,这说明离子注入并未引起元素偏析.Elsayed 等[53]采用常规CDB 技术研究了Cu 在GaAs 半导体中扩散后的缺陷特征,实验发现Cu 是以富集形式存在的.此外,结合PALS 结果可知As 空位附近不存在铜原子,并且半导体中空位复合物不是与Cu 原子结合,而是一种本征缺陷.Xu 等[54]发现在MgO 中注入Au 粒子后会在样品表面形成纳米尺寸的Au 颗粒,通过CDB 结果发现了辐照后产生的空位团簇位于Au 纳米粒子的附近.Slotte 等[55]也采用辐照的方法对氮化铟(InN)进行2 MeV 的He 离子注入,研究结果显示辐照后产生了大量的空位型缺陷和 VIn-nVN复合物,随后结合模拟计算确定了其中一种缺陷为VIn-2VN复合物.Simpson 等[56]在硅中注入氟离子后进行了退火实验,通过CDB 表征出退火产生了氟-空位复合物,且每个空位附近存在2—3 个氟原子.

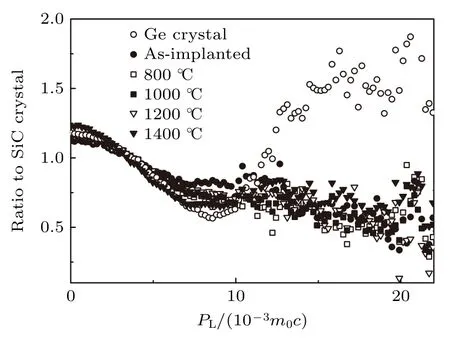
图19 SiC 在不同温度下退火的CDB 谱图[52]Fig.19.CDB spectra of SiC annealed at different temperatures[52].

掺杂也是改善半导体性能的常用手段之一,而空位型缺陷及其演化可以显著改变预期的物理变化方向.Das 等[57]通过溶胶-凝胶法制备了不同浓度Ca2+掺杂MgO 的纳米晶材料,用常规CDB 技术对样品进行表征后发现在低浓度的掺杂下,由于大尺寸的Ca2+离子没有占据Mg2+离子位点会导致新的空位和空位团簇的形成,随着掺杂浓度的升高,材料中缺陷的类型没有发生变化,CDB 结果如图20 所示.此外,他们也结合PALS 技术证明了以上结论.Pasang 等[58]采用PALS 和CDB 技术研究了ZnO 纳米晶体中单掺杂剂和共掺杂剂以及原生缺陷的作用,并讨论了不同电荷态的过渡金属离子掺杂后缺陷对能带的调节作用.

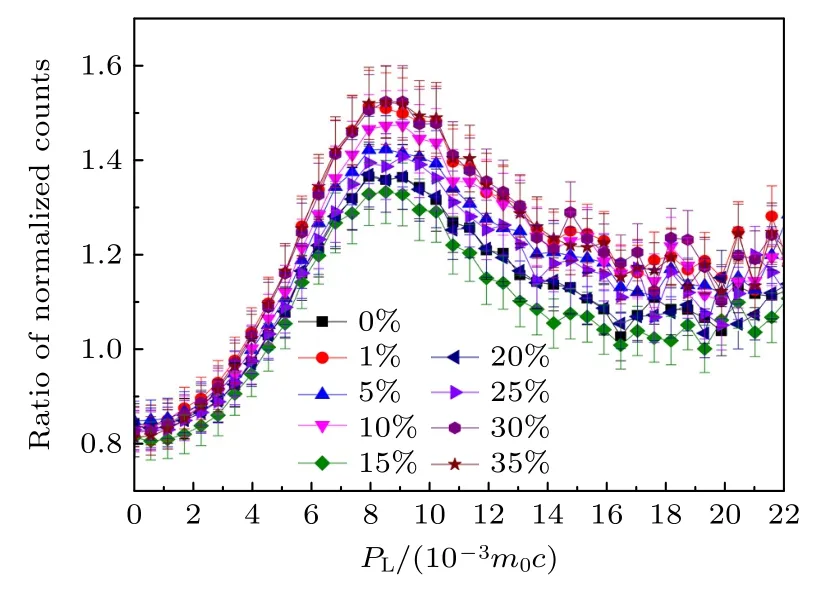
图20 不同浓度Ca 掺杂MgO 样品的CDB 谱图[57]Fig.20.CDB spectra of MgO samples doped with different concentrations of Ca[57].

3.4 常规CDB 技术在聚合物材料中的应用

正电子湮没技术是表征聚合物材料自由体积结构的一类特殊方法.近年来PAS 技术在聚合物材料中的应用越来越广,其中使用CDB 表征的工作也逐渐增多.聚合物分子链间存在自由体积孔洞,这使得聚合物内部电子密度普遍要低于金属和半导体等材料.入射的正电子一部分会在热化阶段后期与二次电子形成一种亚稳态结构-电子偶素(Ps),根据正电子与电子自旋相对取向可以分为仲正电子偶素(p-Ps) 和正电子偶素(o-Ps).图21 为正电子在入射聚合物材料中热化扩散及湮没示意图.相比于其他方法,PAS 技术可以直接测量聚合物中自由体积、孔洞的尺寸、密度及分布.CDB 商谱的高动量部分主要反映了自由正电子与聚合物原子中电子的湮没信息.

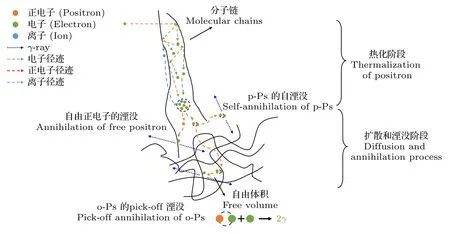
图21 聚合物中正电子的湮没状态Fig.21.Annihilation state of positron in polymer.

Sharma 等[59]采用水溶液浇铸法制备了聚乙烯醇(polyvinyl alcohol,PVA)基氨基功能化多壁碳纳米管(fMWCNTs,质量百分比为0.2%,0.4%,0.8%和1.0%)复合材料,通过常规CDB 技术研究了复合材料中的纳米级分子堆积和微观缺陷.结果如图22 和图23 所示,低掺杂量 PVA 材料的CDB曲线没有明显变化,说明掺杂没有改变纳米孔洞周围的化学环境.但掺杂含量高于0.8%时,发现8.6×10-3m0c处峰值明显下降,分析认为是复合材料内部出现了纳米分子堆积,开空间体积增加,正电子湮没概率增加.

图22 PVA 基纳米复合材料的CDB 谱图[59]Fig.22.CDB spectra of PVA based nanocomposites[59].

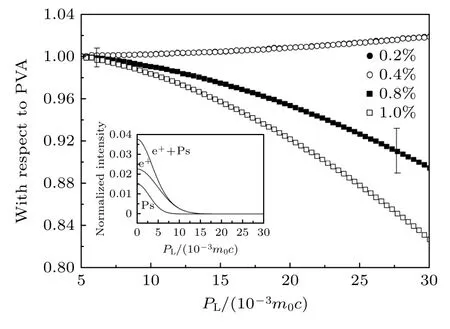
图23 纳米复合材料中自由正电子湮没贡献的CDB 与PVA的比值曲线.插图为纯 PVA 的动量密度分布反卷积[59]Fig.23.CDB ratio curves with respect to PVA obtained for free positron annihilation contribution in the nanocomposites.The inset shows the deconvolution of the momentum density for pure PVA[59].

Xia 等[12]采用溶液铸造法制备了直接与钯阳离子膜交联的壳聚糖(chitosan,CS),通过常规CDB 技术研究了与自由体积相关的亚纳米级分子堆积和 CS-cr-PM 中自由体积纳米孔的化学环境相关信息.Cao 等[60]也制备了CS-Fe3O4纳米复合材料和Cu-CS 材料,并采用CDB 技术证明了带正电的金属离子和CS 分子中的活性基团子对正电子湮没的局部化学环境有很大影响.

Ghasemifard 和Ghamari[61]制备了聚氯乙烯(PVC)-乙酸乙酯(EVA)聚合物共混物后,通过CDB 技术表征出PVA 聚合物和PVA-EVA 聚合物共混物比非聚合物样品表现出更大的自由体积孔洞;且正电子偶素与核芯电子(可能是EVA 氧核芯电子)的湮没有助于探测到样品中的自由体积孔洞.Rana 等[62]采用CDB 技术测试了具有不同相对丰度的聚苯胺(PANI)和氧化石墨烯(GO)的GO-PANI 复合材料的空位型缺陷,结果显示缺陷主要由结合在氧化石墨烯层上的氧空位和来自聚苯胺基体的碳原子组成.此外,研究者还结合PALS 技术测量了正电子偶素的寿命和强度,估算了自由体积缺陷的大小和浓度,发现自由体积分数随聚苯胺丰度的增加而增大,随反应温度的升高而减小.

4 基于慢正电子束流CDB 技术在材料中的应用

常规CDB 技术只能用于表征材料整体的缺陷信息.近年来,基于常规谱仪开展起来的慢正电子束流CDB 技术可通过改变入射正电子的能量,从而探测材料表面、近表面到亚微米深度范围内的开空间缺陷信息,弥补了常规CDB 技术只能表征体效应的不足.慢正电子束流CDB 技术是一种对材料无损、可用于精确测量原子到亚纳米尺度缺陷的类型、尺寸、浓度和深度分布新型核分析技术.慢正电子束流CDB 技术在材料领域的快速发展,为在固体物理、表面物理以及低能电子实验的开展开辟了新道路,同时在凝聚态物理、原子物理、化学、材料和医学等领域也成为了重要的科研工具之一.现阶段,慢正电子束流CDB 技术在金属合金领域中的应用范围最广,同时在薄膜材料中有也涉及.

基于慢正电子束流开展起来的CDB 技术已经应用于金属合金领域中气体原子的信息表征,同时在金属合金领域中表面辐照损伤的研究方面也发挥了重要作用.对核结构材料中金属元素、辐照缺陷和气体原子的表征技术一般有透射电子显微镜,热脱附谱和核反应分析等: 1)透射电子显微镜可检测到辐照诱导偏析、大孔洞或气泡等,但尺寸过小的析出物相结构或者原子尺度的点缺陷、辐照初期气体-缺陷团簇在没有长大前利用电镜很难直接观察;2)热脱附谱可以研究气体在缺陷中的热力学性质、计算气体在材料内部的滞留量,但无法考量气体原子在合金内部的分布情况,并且对样品具有一定的损伤性.利用慢正电子束流CDB 技术可以检测材料表面微观缺陷信息的优势,通过观察商谱图中由于高动量电子的贡献而导致的动量分布变化,就可以识别出合金在经过辐照后引起的表面深度范围内杂质原子与缺陷的相互作用以及缺陷复合物的类型.

不同辐照条件下缺陷的类型或浓度不同,H/He 辐照后样品中会形成H/He-缺陷复合体,其中H/He 原子数与缺陷的比例也不同.Cao 等[63]采用20 keV 的 He 离子辐照了Fe9Cr 合金,结果表明注入的He 原子会与剩余的位错或空位形成复合物,从而在电子动量为PL=11.8×10-3m0c附近出现He 的特征峰.An 等[64]采用30 keV 的H+在不同剂量和温度下对纯Ti 进行辐照,采用6 keV的入射正电子能量的慢正电子束流CDB 技术测量了温度对微观缺陷的影响,结果如图24 所示.在CDB 曲线的高动量区域出现明显的H 相关峰,这是由于正电子与H 和Ti 元素形成的共价键中电子的湮没导致,该研究也认为辐射剂量和温度的增加有助于氢空位复合物的形成.

图24 纯钛样品在RT,473 和573 K 的H 离子辐照至0.2 dpa 时的CDB 谱图[64]Fig.24.CDB ratio curves of the pure titanium specimen H ion irradiated to 0.2 dpa at RT,473 and 573 K[64].

同时,Wang 等[65]也对纯Ti 进行不同时间和电流密度的电化学充氢实验,研究结果表明,CDB能够识别出钛氢化合物和缺陷中氢的存在形式.Fujinami 等[66]用Cu+离子辐照了纯Si 和纯Fe,采用不同入射正电子能量的慢束CDB 技术表征了Fe 中V-Cu 的缺陷结构.Beyerlein 等[67]采用慢正电子束流CDB 技术表征了辐照前后Mg 基合金中的晶体缺陷及化学环境的变化,发现离子辐照没有诱导合金中的原子团聚.Liu 等[68]用不同能量的He 离子辐照金属W 和W5Re,采用慢正电子束流CDB 技术表征了Re 原子对W 中He 原子与辐照缺陷相互作用的影响.与未辐照的W-Re 相比,He 离子辐照的W-Re 合金中都出现了Re 相关峰,但辐照后合金中的Re 相关峰较低,这表明Re 原子会与空位形成Re 空位络合物,进而有效地抑制空位型缺陷的迁移和生长.Ren 等[69]采用2.8 MeV 的 Fe 离子在不同温度下辐照了CoCrFeMnNi 合金,并用入射能量为16 keV 的慢正电子束流CDB 技术研究了缺陷的演化,CDB结果如图25 所示.离子辐照后产生了大量的空位团簇,随着辐照温度的升高,空位回复过程和产生过程同时发生.高动量区并未出现明显的峰,这表明合金中无辐照诱导偏析现象发生.

Zhang 等[70]对Ti/Al 多层膜在不同温度热处理后的膜层间元素的扩散现象进行了探测,采用入射能量为1.7 keV CDB 技术研究了热处理后薄膜结构和各层缺陷的变化.如图26 所示,随着退火温度的升高,空位型缺陷逐渐回复,且位于PL=12×10-3m0c处Ti 的特征峰值逐渐升高,这表明Ti是Ti/Al 高温退火合金化过程中的主要扩散物质.

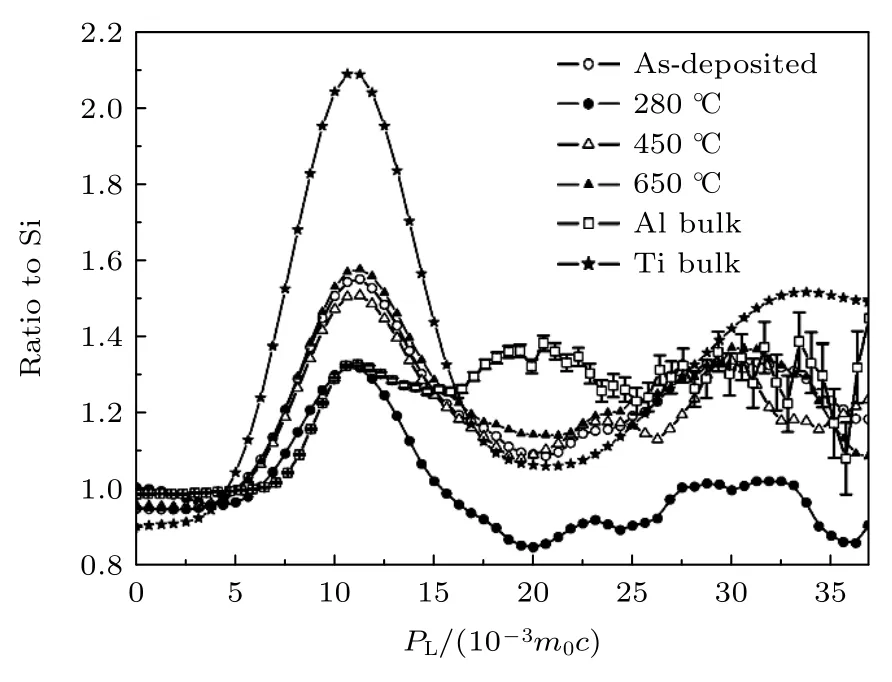
图26 不同退火温度下Ti/Al 界面的CDB 谱图[70]Fig.26.CDB spectra of Ti/Al interface at different annealing temperatures[70].

Reiner 等[71]对Au/Cu 双层膜进行不同温度退火,研究了膜中的开空间缺陷和元素演化,CDB谱显示回火过程中伴随着Au 薄膜缺陷的回复、Au 与Cu 发生合金化,他们还经过结合理论计算确定了合金膜成分为Au0.7Cu0.3.Khanam 等[72]通过CDB 技术研究了不同温度下原子层沉积生长的TiN/TiO2/a-Si 异质结构中开空间缺陷特征的差异.研究结果显示不同温度下生长的TiO2薄膜的正电子湮没特征与生长过程中TiO2和a-Si 层的混合以及在界面处形成的SiO2薄层无关.且随着生长温度的升高,TiO2层中开空间缺陷的数量增加.杨静[73]用伽马辐照了几种聚合物 (LDPE,PEEK 和FEP),随后进行了CDB 测试.分析发现这几种样品在辐照前后的CDB 曲线特征相似,说明正电子的湮没环境并未发生改变.

5 理论计算多普勒谱在材料方面的应用

CDB 谱在金属合金等材料中元素偏析的演化机制、开空间缺陷的结构特性和间隙原子与空位型缺陷相互作用等表征方面展示出了巨大优势.然而,这些信息是通过CDB 曲线的变化间接表征,还需要补充更直接的证据来充分地分析实验结果.第一性原理计算就是分析CDB 谱的重要工具.随着CDB 技术在各个领域的广泛应用以及计算机科技的快速发展,近些年关于正电子理论计算方面的工作逐渐增多,如利用第一性原理、分子动力学和动力学蒙特卡罗等多种方法进行建模,关注溶质原子的扩散和结构、空位型缺陷的尺寸和浓度、空位-杂质原子的类型等信息.这些创新性的工作可以弥补正电子湮没技术在理论研究方面的不足,又能将实验结果与理论研究相结合,这增强了实验结果的可靠性.

标准密度泛函理论(density functional theory,DFT)只考虑电子密度这一组元,然而计算正电子湮没的多普勒展宽,需要同时确定系统中的电子和正电子的密度和波函数.这两个参量通常用双组元密度泛函理论 (two-component density functional theory,TCDFT)计算得到,其中正电子密度是第二组元[74-76].TCDFT 的总能量可表示为

其中,F[n+]和F[n-]分别是正电子和电子的单分量泛函;vext是一种外部势(external potential),是电子-正电子相关泛函.经修正的Kohn-Sham 方程计算可以将体系总能量最小化,如下所示:

其中,ϕ可以表示为

电子和正电子密度表示为

在对材料中的正电子进行建模时,基于两个主要假设.第一个假设是正电子不影响固体中的电子密度;第二个假设是零正电子密度极限(zeropositron-density limit),即正电子密度在无缺陷晶格和缺陷中都被认为接近零.首先,用标准DFT求解电子密度;其次,正电子态在势中求解

其中,ne为电子密度;Vcorr为电子-正电子相关势的零密度极限(zero-positron-density limit).对于具有空位型缺陷的体系(如单空位和空位溶质配合物),正电子引起的离子排斥力也包括在计算中.正电子对离子产生的力j为最低正电子能量特征值(ε+)对应(14)式的势[76].正电子诱导力表示为

其中,ψp是正电子波函数,H(r)为正电子的单粒子哈密顿量.V+(r)用原子叠加法近似为

λ 是湮没率,re是经典的电子半径,c是光速,γ(ne(r))是增强因子(enhancement factor).动量分布ρ(p)利用状态依赖(state-dependent)模型和PAW (projector augmented-wave)方法计算了湮没电子-正电子对的动量分布ρ(p),表示为

其中ψj(r)是轨道j上电子的波函数,,其中λj是轨道j上电子的湮没率.是使用独立粒子模型(independent-particle model,IPM)计算的湮没率,其中γ≡1.此外,一般采用Boronski-Nieminen 局部密度近似来计算电子-正电子相关和增强因子(enhancement factor).经过计算得到的动量分布与实验对应的半高宽(fullwidth-at-half-maximum,FWHM)处的高斯函数进行卷积,其中半高宽应与实验分辨率相对应,最后获得的多普勒谱就表示为归一化后的动量分布比值曲线[77,78].

Simula 等[76]提出了一种变分量子蒙特卡罗方法来模拟半导体和绝缘体中湮没电子-正电子对的动量密度.通过比较氮化铝和硅中511 keV 2γ湮没线多普勒展宽的计算结果与参考样品的实验数据发现,这种模拟方法比传统方法更接近实验结果,并证明了电子-正电子相关的直接建模对于支持正电子湮没光谱理论至关重要.Yang 等[79]采用TCDFT 计算了钨中不同尺寸空位簇的多普勒谱,并与实验结果进行了比对,其中S和W参数值均从多普勒谱中提取.如图27 和图28 所示,在至多15 个空位时,随着空位团簇逐渐增大,S参数增大而W参数减小,并且S参数变化趋势明显.但当空位数超过15 个时,空位团簇的大小对S和W参数的影响不明显,如V15和V65的(S,W)点距离较近,这说明空位数为15 时出现了正电子信号饱和.此外,他们的研究从实验方面证明了模拟计算的可靠性,也为后续研究金属材料中的空位团簇信息提供了思路.

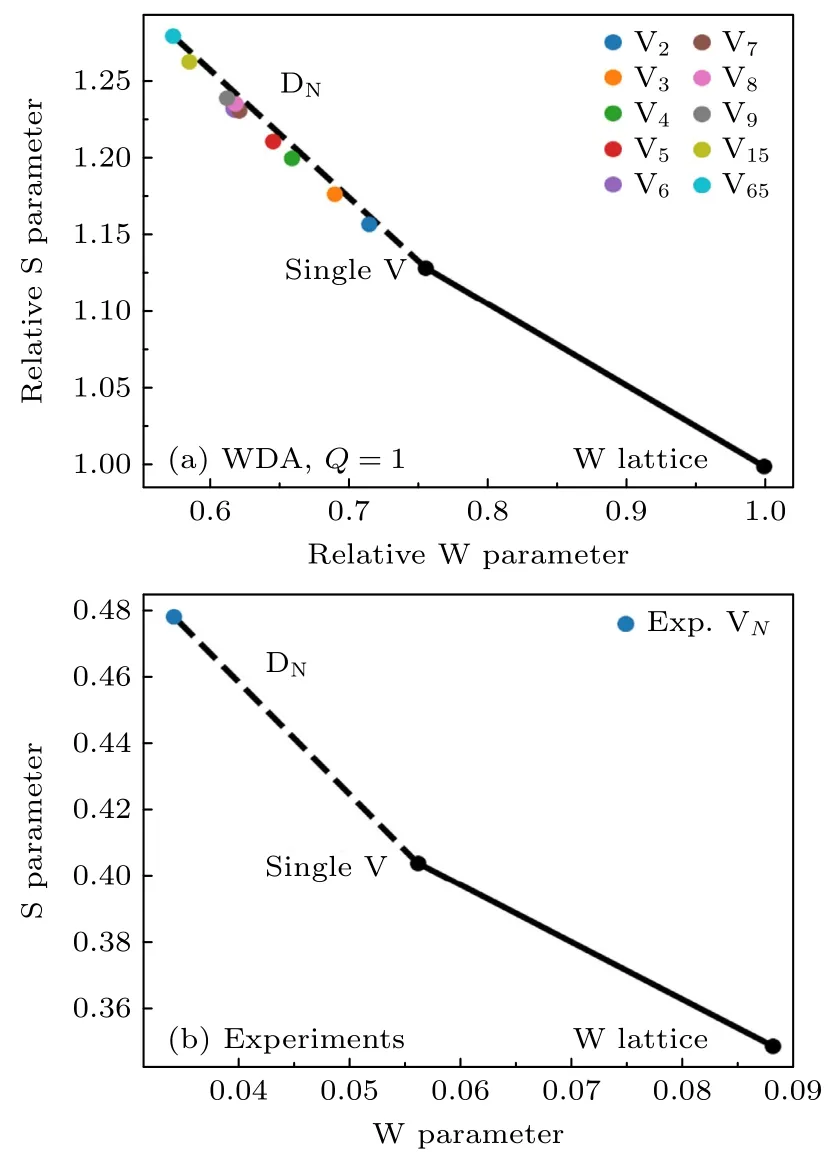
图28 (a) 根据多普勒谱计算的计算S 和W 参数[79];(b) 钨晶格、单空位和VN 的实验S 和W 参量[79]Fig.28.(a) Computed S and W parameters calculated from Doppler spectra[79];(b) experimental S and W parameters for tungsten lattice,single vacancy and VN[79].

Liu 等[80]采用TCDFT 模拟了纯W 中不同占比的He-空位复合物的多普勒谱.如图29 和图30所示,随着空位数量越多,低动量区越高;He 原子数量越多,位于高动量区PL=10.86×10-3m0c—18.10×10-3m0c(1.5—2.5 a.u.)的He-空位复合物的峰值越高.该研究认为He 加入空位团簇中会影响正电子湮没位置附近的电子动量密度.

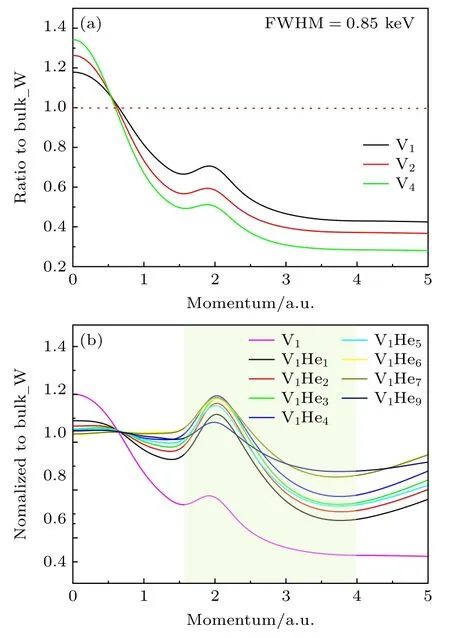
图29 (a)有不同数量空位的纯钨多普勒谱曲线[80];(b)有不同空位/He 原子比值的纯钨多普勒谱曲线[80]Fig.29.(a) Doppler spectra of pure tungsten with different numbers of vacancies[80];(b) Doppler spectra of pure tungsten with different vacancy/He atom ratios[80].

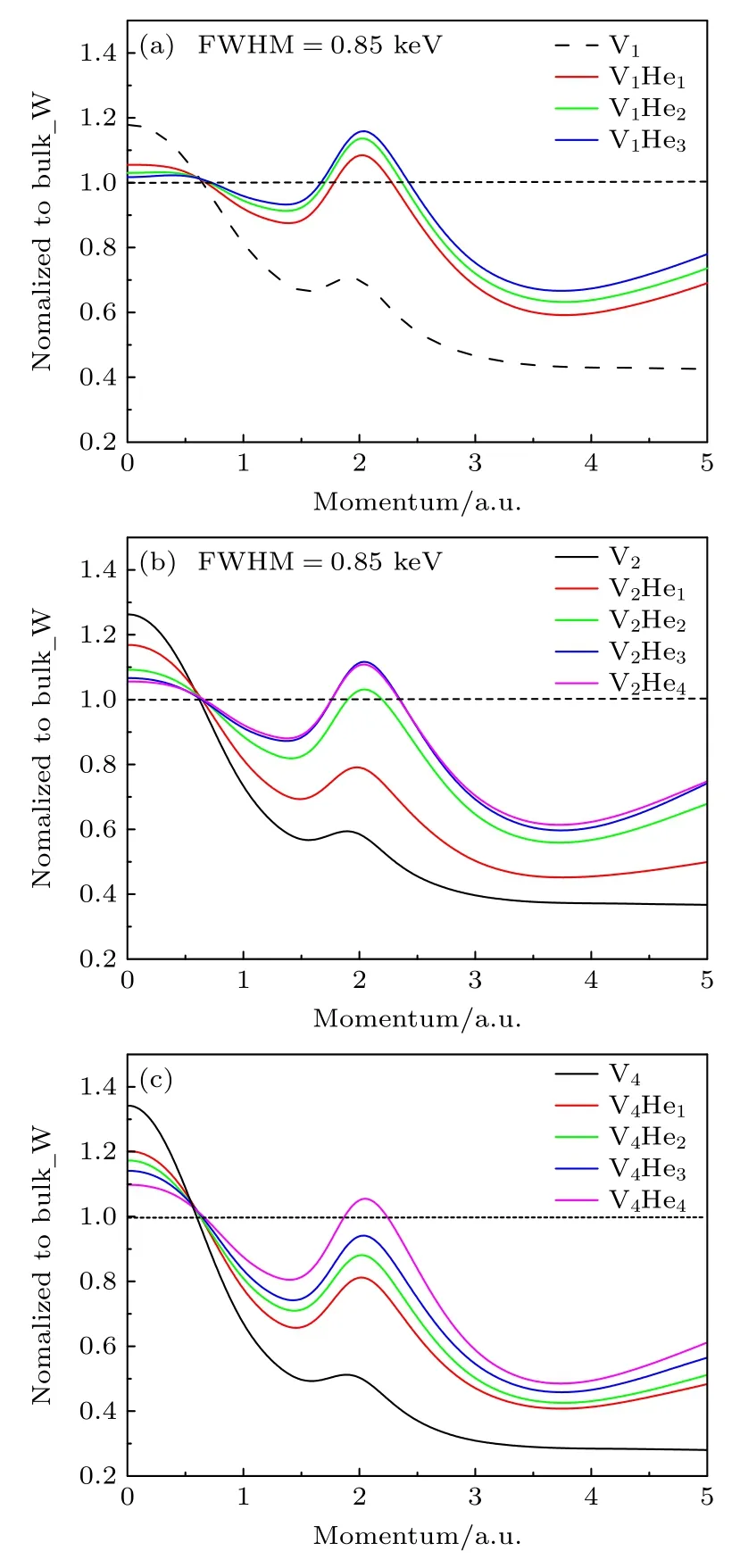
图30 纯钨中有不同空位/He 原子比值下的多普勒谱曲线[80]Fig.30.Doppler curves of pure tungsten with different vacancy/He atom ratios[80].

Fe-Cu 合金是各种应用领域结构部件的模型材料,但是Cu 析出导致的合金硬化和脆化是制约其广泛应用的关键因素,因此,了解Cu 析出物的形成和演化至关重要.正电子湮没谱正是研究Cu 均相和非均相析出成核阶段的有力工具,这是其他检测技术几乎无法达到的.而采取实验和理论计算相结合的方法检测空位、空位团簇和空位-Cu 配合物对于更好地理解、建模和预测合金中Cu 的析出动力学具有重要意义.Yang 和Olsson[81]利用TCDFT 研究了Fe-Cu 合金中无空位Cu 团簇和非均匀空位-Cu 复合物的正电子湮没特征.计算结果显示含随着Cu 原子数量的增加,位于约25×10-3m0c处Cu 特征峰强度逐渐增高,说明空位-Cu 复合物的尺寸逐渐长大,如图31 所示.此外,通过模拟计算再现了等时退火过程中的小尺寸Cu 团簇的演变,并鉴定了Cu 析出物的类型和尺寸.

图31 (a) fcc Cu 和V1-Cu1-8 的多普勒谱[81];(b)两种不同晶格常数下fcc Cu,V1-Cu14-50 和fcc Cu,bcc Cu 晶格中单空位的多普勒谱[81]Fig.31.(a) Doppler spectra of the fcc Cu and V1-Cu1-8[81];(b) Doppler spectra of the fcc Cu,V1-Cu14-50 and single vacancy in fcc Cu and bcc Cu lattice with two different lattice constants[81].

实验的CDB 谱结果和理论计算结果结合分析是表征合金中开空间缺陷和溶质原子非常有价值的工具,这对检测GaN,InN 等半导体中的阳离子空位缺陷和鉴定缺陷杂质复合体的类型也同样适用.Elsayed 等[82]采用TCDFT 软件研究了淬火后原子含量为Al-0.005% In 和Al-0.025% In 和Sn中空位和溶质原子的相互作用,研究结果显示原子含量为0.025% In/Sn 掺杂合金中的空位团簇更多,这导致其多普勒曲线的低动量区(PL≤3×10-3m0c)比原子含量为0.005% In/Sn 略高.如图32 和图33 所示,两种掺杂合金的高动量区(PL≥10 ×10-3m0c)分别略高于V-In/V-Sn 复合物的模拟计算值,而低于V-2In/V-2Sn 复合物的模拟计算值,这表明在淬火态的Al-In/Al-Sn 合金同时含有两种缺陷.此外,他们还通过计算结合能确定了合金中的主要缺陷是V-In/V-Sn 复合物.

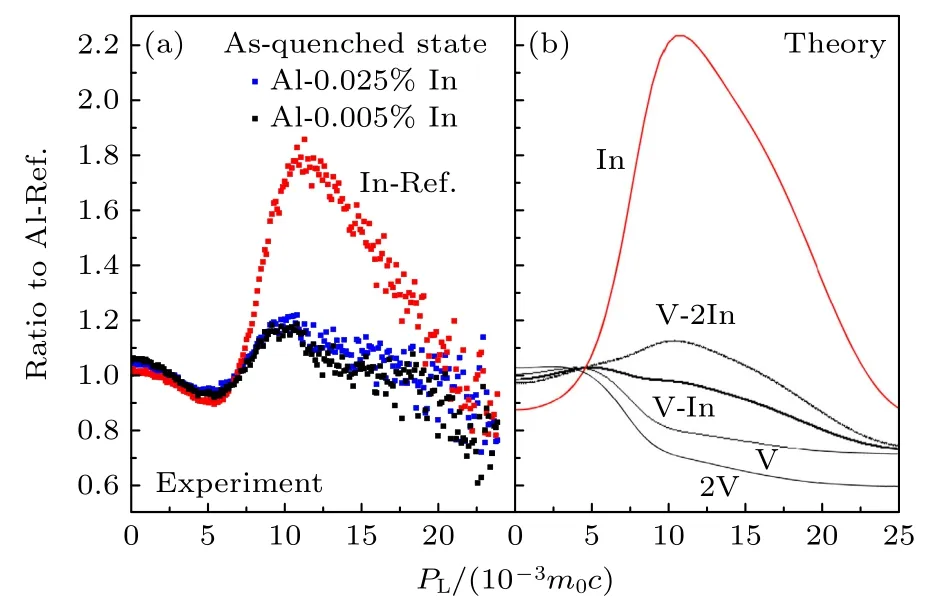
图32 (a) Al-In 合金在淬火后以及纯In 的多普勒谱图[82];(b) 模拟计算的单空位和双空位以及空位-In 复合物的多普勒谱图[82]Fig.32.(a) Doppler spectra of Al-In alloys after quenching as well as the spectrum of the pure indium reference[82];(b) calculated ratio curves with respect to Al for mono-and di-vacancies as well as for vacancy-In complexes[82].

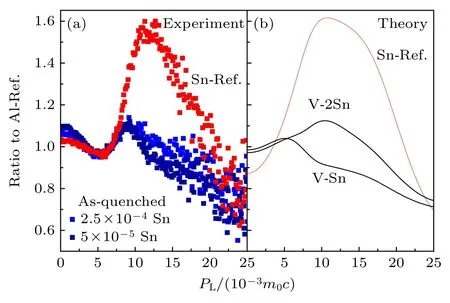
图33 (a) Al-Sn 合金在淬火后以及纯Sn 的多普勒谱图[82];(b) 模拟计算的单位和双空位以及空位-Sn 复合物的多普勒谱图[82]Fig.33.(a) Doppler spectra of Al-In alloys after quenching as well as the spectrum of the pure indium reference[82];(b) calculated ratio curves with respect to Al for mono-and di-vacancies as well as for vacancy-In complexes[82].

Elsayed 等[83]采用模拟计算和实验相结合研究了Zn 掺杂GaAs 的点缺陷特征,他们认为开空间缺陷附近存在的Zn 原子导致多普勒曲线的高动量((20—30)×10-3m0c)区呈现散射.如图34 所示,随着加入的Zn 原子数量增加,VAs-ZnGa复合物的曲线峰值也随之增加,且VAs与VAs-ZnGa的曲线非常接近,说明掺杂的Zn 存在于形成复合物的VAs附近.此外,VAs-ZnGa的动量分布曲线与Zn掺杂GaAs 样品的动量分布曲线非常接近,这说明陷可能是VAs-ZnGa,他们还结合正电子湮没寿命结果证实了这一观点.

图34 (a) Zn-扩散GaAs(淬火态)和纯Zn 样品的多普勒谱图[83];(b) 理论上计算了GaAs 中不同空位和空位配合物的动量密度[83]Fig.34.(a) Results of Doppler broadening spectroscopy of Zn-diffused SI GaAs (as-quenched) and pure Zn samples[83];(b) ratio of the momentum density to bulk GaAs for different vacancies and vacancy complexes in GaAs are theoretically calculated[83].

Rauch 等[84]计算了氮化铟中铟空位(VIn)和氮空位(VN)以及混合空位团簇中湮没电子-正电子对的动量分布.研究结果显示,空位VN和空位数高达4VN的VN簇不能捕获正电子,而铟空位VIn和混合空位团簇是有效的正电子陷阱.2006 年,Makkonen 等[85]表征了高浓度锑(Sb)掺杂Si 中的空位杂质配合物,通过模拟计算得出的CDB 谱峰值强度推算出了空位附近Sb 原子的数目.此外,他们研究了GaN 中不同杂质原子(O,H)对Ga空位的影响.Slotte 和Tuomisto[86]也研究了掺锑的Si 样品中开空间缺陷在退火前后的演化,通过实验结果和理论计算结合的方法表征出辐照后的样品中存在V-Sb 复合物,但在600 K 退火后VSb 复合物逐渐迁移并聚集形成了V-Sb2配合物.Linez 等[87]采用从头算法研究了6H-SiC 和两种氮空位配合物的6 种基本空位型缺陷的正电子湮没特性(寿命和多普勒展宽),也证实了CDB 技术可适用于观察硅空位-氮复合物VSiNC和碳空位配合物VCCSi.

6 结语

本文综述了常规CDB 技术在表征金属/合金、半导体和氧化物等材料中微观缺陷演化以及元素偏析等方面的进展.同时也总结了慢正电子束流CDB 技术在金属/合金与薄膜等功能材料领域的研究进展.由于慢正电子束流CDB 技术在选定深度上的微观缺陷探测的灵敏度大大提高,它在测量纳米深度范围内的缺陷信息,尤其是对特定深度以及界面处的缺陷表征表现出极大的优越性.该技术逐渐成为了结合三维原子探针、透射电子显微镜和扫描电子显微镜等检测方法研究材料中微观缺陷和微观结构特征的利器.但在实验方面CDB 技术也存在不足之处,它无法给出空位型缺陷和溶质原子团簇的类型和尺寸,而材料中微观缺陷会影响其宏观性能,如机械性能,若能表征点缺陷的浓度和大小,就可以预测材料中微观结构的演变,这将对材料从微观机制角度解释其物理性能的演化机理大有裨益.目前,CDB 技术在理论研究方面的工作仍较少,对于一些实验结果的理解仍需进一步的剖析,若根据第一性原理和蒙特卡罗等方法模拟正电子在各类材料中的湮没信息,并综合其他表征手段得到的实验数据建立相应的理论模型,这将对CDB 技术的快速发展和材料科学的进步大有裨益.

感谢中国科学院高能物理研究所正电子湮没平台对本文的支持.