反比例函数图象中的一个基本图形的应用

⦿ 陕西省安康市高新区第一初级中学 贾 文

1 基本图形与结论展示

图1

证明：四边形OABD的面积S=S△AOC+S梯形ACDB.

从另一角度,四边形OABD的面积S=S△AOB+S△BOD,而S△AOC=S△BOD,所以S△AOB=S梯形ACDB.

2 运用结论,简洁明快

2.1 与矩形结合,求点的坐标再运用

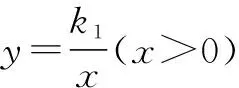
图2

分析：先求出点A的坐标,再求出反比例函数的解析式,那么,点E,F的坐标均可求出,问题便迎刃而解.

解：由D(0,4),B(6,0),知点C的坐标为(6,4).如图3,过点A作AH⊥OB于点H.

图3

而CB=4,OB=6,易求得AH=2,OH=3,因此A(3,2).

又xF=6,那么yF=1,因此F(6,1).

点评：解决本题的关键在于如何求出点A的坐标,本例运用几何法作平行线并利用三角形相似求出.如果直接用中点公式求点A坐标,则解法更简捷,但初中课本未明确给出,部分学生对中点公式比较陌生.

2.2 与平行四边形联姻,构造相似运用

图4

分析：平行四边形的对边相等且平行,利用C,D两点都在反比例函数的图象上,从点C,D作x轴的垂线,会产生相似三角形,并且可用含有k的式子表示其坐标,再利用本文的基本图形解决.

解：如图5,从点C,D分别作x轴的垂线,垂足分别为E,F.

图5

因为OC∥DA,所以∠COE=∠DAF,∠CEO=∠DFA.

点评：本题运用平行四边形和中点的条件构造直角三角形相似,用含有参数的式子表示C,D两点的坐标,根据△COD的面积为6,再利用本文的结论,问题得以快速解决.

2.3 与几何最值相联

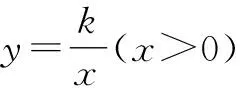
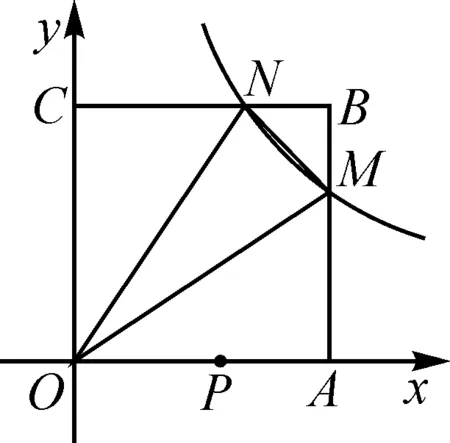
图6

分析：观察题目的图形,可利用本文的基本结论和已知条件,求出M,N两点的坐标,那么就转化为“两定一动”型问题,根据“将军饮马”图形作其中一个定点的对称点,转化为“两点之间,线段最短”来解决.

图7

作点M关于x轴的对称点E,连接NE交x轴于点P,由对称性知PM=PE,则NP+MP=NP+PE=NE.

由“两点之间,线段最短”,知NE的长即是PM+PN的最小值.

点评：本题的图形与“基本结论”中的图形高度吻合,因此运用基本结论会得心应手.当然,本题的另一解法是分割法,由△OMN的面积等于正方形OCBA的面积减去3个直角三角形(△OCN,△NBM,△OMA)的面积之差,再综合运用其他条件和所学知识解题.

2.4 与一次函数贯通

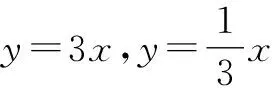
图8

A.6 B.8

C.4 D.6.5

分析：根据已知条件,只要能求出点A、点B的坐标,再利用本文的基本图形,则问题获解.

又点A,B都在第一象限,那么b=3a,则B(3a,a).

如图9,过点A作AC垂直x轴于点C,过点B作BD垂直x轴于点D.由本文的基本结论,可知S梯形ACDB=S△AOB=8.

图9

故选:A.

点评：本题根据点A、点B在一次函数和反比例函数的图象上的特点,运用k的不变性建立方程,求得点的横纵坐标的关系,再运用本文结论解决问题.

2.5 与全等三角形携手

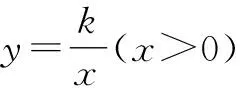
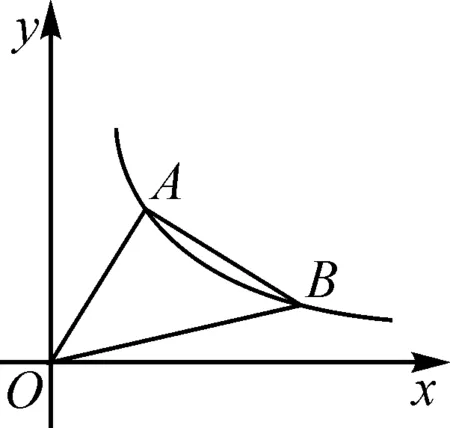
图10

分析：要求△OAB的面积,结合本文基本图形,求出点A、点B的坐标是解题的关键.结合等腰直角三角形的条件,构造“一线三垂直”的全等图形,得出相等的线段,再将点A,B坐标用字母n表示出来,运用反比例函数系数k值的不变性建立方程即可.

解答：略.

在平时的解题基础上,我们要立足题目的解答,深度思考,挖掘出简单图形的丰富内涵,进而借题发挥,通过建立各种图形与知识的联系,起到将综合问题分解、简化的作用.关注核心知识,关注基本图形,加强思维引导,将方法、技能落到实处.Z