折出60°的角

陶琼

折纸做60°、30°、15°等特殊角是在学生学习了“三角形”“四边形”“轴对称”等基本概念、性质的基础上，进一步研究图形翻折的一次数学活动。在此之前，教材已呈现折角平分线，折纸研究轴对称图形特点、全等图形性质等活动。折纸有助于学生体会研究图形性质实际上就是揭示图形中各几何要素之间的关系，明确观察、实验、猜想、证明是几何研究的基本活动，感悟“用合情推理发现结论，用演绎推理证明结论”这一几何研究的基本思考方式。本节课的教学重点是用不同的方法折出60°的角并说明理由，有了60°的角，再通过对折得到30°、15°的角。

一、视频导入，创设折纸情境

教学伊始，笔者让学生思考不借助任何测量工具，在一张矩形纸片上折出一个正方形的方法，随后播放演示视频，让学生观察折的过程中，折出了多少度的角。学生观看视频后，都能发现折出了45°角。笔者顺势鼓励学生动手折一折，大部分学生都能将矩形沿着对角线对折，很快折出45°角。笔者肯定了学生折45°角的方法，并在用几何画板演示折角过程后追问：如图1所示，哪些角等于45°？你还发现了哪些度数的角？折痕AE可以看作对称点B与B'的什么？折叠前后的两个对应图形有什么关系？

学生很快发现：∠BAE、∠EAD、∠AEB、∠AEB'都等于45°；计算得到∠AEC=135°；折痕AE可以看作B与B'的对称轴；折叠前后两个图形全等。

45°角的折法让学生识别出折痕的本质，意识到对折可以平分一个角。最后，笔者追问：按照同样的方法，你还可以折出哪些角呢？有了刚才折45°角的活动经验，学生很快通过对折折出了22.5°，11.25°等“倍分”的角，为后面折出60°角后对折得出30°、15°的角做铺垫。

二、设置问题支架，引导动手操作

教学中，笔者设计主问题：能不能像折45°角那样，不借助任何测量工具，仅用一张矩形纸片准确地折出60°角呢？折60°角对学生而言难度比较大，笔者通过设置问题支架，引导学生动手操作。

问题支架1：我们学过的什么图形里有60°角呢？

在已学的特殊三角形中，学生想到等边三角形和有30°角的直角三角形里有60°角，从而打开了思路。

问题支架2（思路一）：如何用一个矩形纸片折一个等边三角形呢？

笔者引导学生回想刚才折45°角的过程：我们可以折出一个正方形，得到4条相等的边。学生顺势思考如何让正方形4条边中任意3条“聚”在一个三角形里，进而折出等边三角形，得到60°角。学生尝试折纸后展示折法，笔者用多媒体演示折叠过程（如图2）。

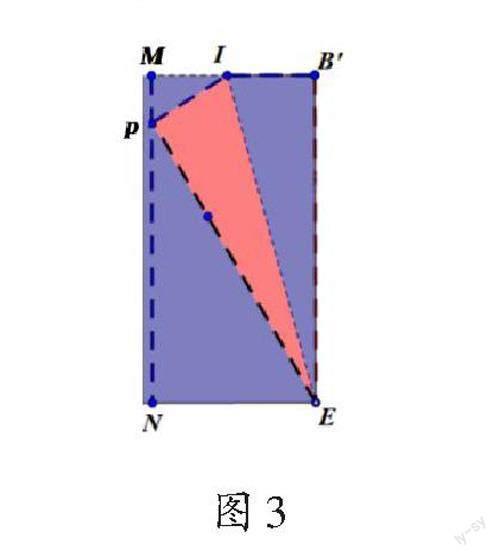
问题支架3（思路二）：我们将图2中的正方形沿着折痕MN对折，观察图形（如图3），此时∠PEN还等于60°吗？PE和EN有什么数量关系？

学生回答：∠PEN仍然等于60°，PE=2EN。接着，笔者引导学生分析：∠PNE=90°和PE=2EN是因，∠PEN=60°是果，并让学生证明。

学生根据之前学习的特殊四边形以及直角三角形的性质等，很快证出这个推论。接着，学生尝试折纸，小组交流合作，构造斜边是直角边2倍的三角形。

折法一：（如图4）对折矩形ABCD，使AD与BC重合，得到折痕EF，把纸片展平，再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到线段BN。

笔者追问：观察折痕EF与AB的关系，你还有其他证法吗？写出已知、求证，并完成证明。学生写出“已知：如图5，在矩形ABCD中，EF垂直平分AB，△ABM与△NBM关于BM轴对称，点N在EF上。求证：∠ABN=60°”。学生识别出折痕的本质就是对称轴，想到EF是AB的垂直平分线，于是想到连接AN（如图5）。

学生上讲台板书证明过程：连接AN，因为EF垂直平分AB，所以AN＝BN；又因为△ABM与△NBM关于BM轴对称，所以AB=BN；可得AB＝BN=AN，△ABN是等边三角形，所以∠ABN＝60°。

笔者继续追问：刚才的折纸过程是将矩形纸片对折一次，如果对折两次，你还可以折出60°角吗？学生先独立思考，设计方案，解决问题，再在小组中交流自己的折法。学生上讲台展示折法，笔者用多媒体演示折叠过程。

折法二：（如图6）将矩形纸片对折两次，得到三条折痕，分别为MN、EF、GH，再一次翻折，使点B落在MN上，并使折痕经过点E，从而得到∠AEB′＝60°。

笔者通过折纸活动，让学生经历思考、操作、观察、猜想、验证的活动过程，体会到转化思想。不同折法让学生体验到方法的灵活性，用不同方法证明折法的过程培养了学生的创新思维。

问题支架4：同学们已经学会了折60°角，你能折出30°、15°角吗？你还能折出其他度数的角吗？

通过小组交流，学生认识到通过对折可以得到60°角的“倍分”角，进一步体会到对折的实质是轴对称，可以将角平分，继而得到“和差、倍分”的角。

三、拓展巩固，积累数学活动经验

为帮助学生积累数学活动经验，笔者先让学生归纳、梳理本节课中用矩形纸片折出了哪些特殊度数的角，如何折出60°的角，具体用到了哪些知识；再出示由易到难的三类练习题。

【基础性练习】如图7，把一个正方形的纸片对折两次，然后剪下一个角。要得到一个正方形，剪口与折痕应成多少度角？

【巩固性练习】如图8，乐乐用一张长方形纸片折纸飞机，折叠过程如图8所示，则∠ACB的度数为        。

【提高性练習】如图9-1，对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平；再一次折叠纸片，使点A落在EF上的点N处，并使折痕经过点B，得到折痕BM，把纸片展平，连接AN。折痕BM   （填“是”或“不是”）线段AN的垂直平分线。

如图9-2，继续折叠纸片，使点A落在BC边上的点H处，并使折痕经过点B，得到折痕BG，把纸片展平，则∠GBN＝    °。

如图9-3，折叠矩形纸片ABCD，使点A落在BC边上的点A'处，并且折痕交BC边于点T，交AD边于点S，把纸片展平，连接AA'交ST于点O，连接AT。求证：四边形SATA′是菱形。

基础性练习题来自课后习题，考查折痕的实质以及正方形的判定；巩固性练习题是学生日常生活中比较熟悉的折纸飞机，考查折叠前后两个图形全等的基本性质；提高性练习题是在折60°角的基础上设计的变式练习。这三道题与本节课内容呼应，可以考查学生对本节课内容的掌握程度。

最后，笔者出示手折玫瑰花的图片和折纸教程的二维码，让有兴趣的学生课后参照视频教程，尝试折出一朵玫瑰花。

（作者单位：武汉市新洲区思源实验学校）

责任编辑  孙爱蓉