基于增强型龙格库塔优化算法的跳频序列设计
张毅恒, 刘以安, 宋海凌
(1. 江南大学人工智能与计算机学院,江苏 无锡 214122; 2.海军研究院 北京 100161)
0 引言
随着电子对抗技术的发展,干扰技术愈发成熟,使得无线电信号越来越容易被非法接收机干扰、测向和截获。跳频技术以其优秀的抗干扰性能和多址组网性能在军用雷达、民用移动通信、激光雷达等电子信息系统中得到了重要应用[1-3]。跳频序列(FHS)作为控制载波频率跳变的关键,其性能与跳频系统的性能直接相关,因此,设计性能良好的跳频序列一直以来是国内外学者研究的重点。
理想的跳频序列应具有良好的性能指标,如汉明相关性、复杂度、均匀性、平均跳频间隔等。传统跳频序列使用分圆法[4-5]、中国剩余定理[6-7]、m序列[8-9]等方法设计,仅能满足汉明相关性最低。而使用混沌系统[10]、改进祖冲之算法[11]设计跳频序列,虽然提高了复杂度,但无法保证均匀性等其他指标。
针对此局限性,许多研究者使用启发式优化算法设计跳频序列:文献[12]利用粒子群优化算法对三维混沌系统的加权因子进行优化,但参与优化的指标较少;文献[13]利用粒子群优化算法对组合跳变随机平移(CHRS)方法的初始值进行优化,但产生的跳频序列受制于混沌序列的性能,不能充分寻优;文献[14]基于平均干扰功率、均匀性、汉明自相关性和跳频增益构建优化模型,利用改进灰狼算法得到跳频序列,但其目标函数只能针对固定干扰,且搜索精度不高。可见,目前关于跳频序列设计的研究存在参与指标少、寻优性能不足的缺点。
近年来,涌现出许多具有较强寻优能力的启发式优化算法。AHMADIANFAR等[15]于2021年提出龙格库塔优化算法(RUN),该算法的主要思想是基于四阶龙格库塔法计算出斜率作为搜索方向,并基于强化个体质量机制建立种群的更新规则,具有数学理论基础坚实、寻优能力强等优点。虽然RUN性能优秀,但作为一种启发式优化算法,其在复杂问题上仍有易陷入局部最优、收敛速度慢的缺点。
针对以上问题,本文提出一种基于增强型RUN的跳频序列设计方法,主要工作如下:1)考虑跳频序列的多项性能指标,基于汉明相关性、复杂度、均匀性和平均跳频间隔对跳频序列设计进行建模,构建目标函数;2)对标准RUN做出改进,提出增强型龙格库塔优化算法(ERUN),利用混沌反向学习来建立算法的初始种群,提高算法的寻优稳定性;3)基于二次插值法改进个体的更新方向,提高算法的收敛速度和寻优能力;4)基于自适应t分布对更新后的个体进行针对性扰动,帮助算法跳出局部最优;5)基于ERUN对跳频序列设计模型进行优化,得到具有优秀性能指标的跳频序列,降低跳频系统在不同干扰环境中的误码率。
1 跳频系统模型及跳频序列设计模型
1.1 跳频系统模型
设跳频系统有q个频点,频点集为F={f0,f1,…,fq-1},跳频序列长度为l,使用频点集中频点的跳频序列S={s0,s1,…,sl-1}。
在发送端,经调制后的双极性信号为a(t),假设使用根升余弦滚降滤波器对信号进行脉冲成型,发送信号可表示为:
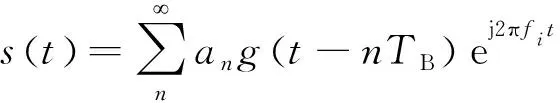
(1)
其中:an为a(t)的第n个信息码;g(t)为根升余弦滚降滤波器的冲激响应;TB为信息码元宽度;fi为信号第i跳的载波频率。
在加性高斯白噪声(AWGN)信道传输中,存在加性高斯白噪声n(t)和干扰信号J(t),进入接收机的信号可表示为:
r(t)=s(t)+n(t)+J(t)
(2)
在接收端,使用与发送端相同的跳频序列控制频率跳变产生共轭信号,并与接收信号混频,得到解跳后的信号r′(t):
r′(t)=(s(t)+n(t)+J(t))e-j2πfit=

(3)
其中:n′(t)和J′(t)分别为经过混频后的加性高斯白噪声分量和干扰信号分量。
对解跳后的信号进行匹配滤波后,噪声分量和干扰信号分量就不再是有效的中频信号,杂散频率被滤除,从而减小了噪声和干扰的影响。
1.2 跳频序列性能指标
跳频序列的汉明相关性表征了序列内频点发生碰撞的次数。对单个跳频序列而言,其汉明自相关值越小,抗干扰性能越强。基于不同时延τ,跳频序列的汉明自相关值HS(τ)和最大汉明自相关值H(S)为:
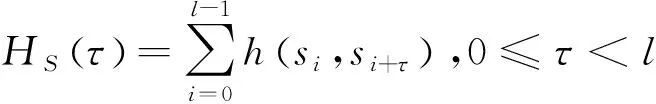
(4)
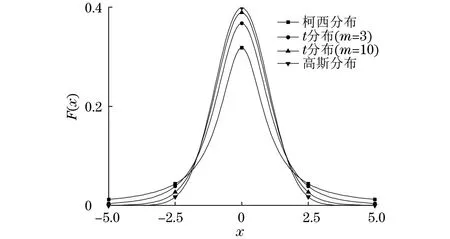
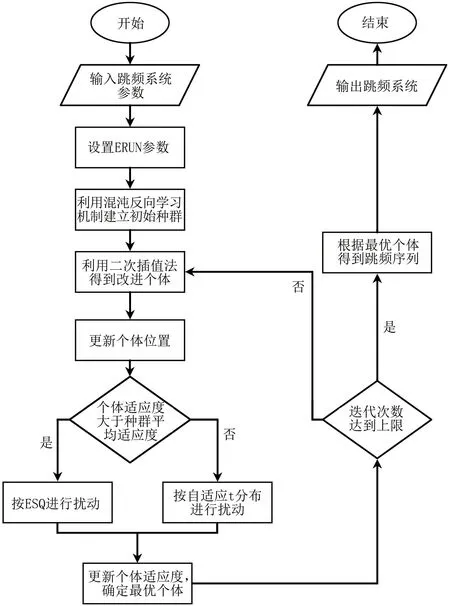
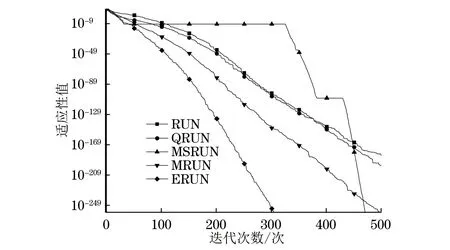
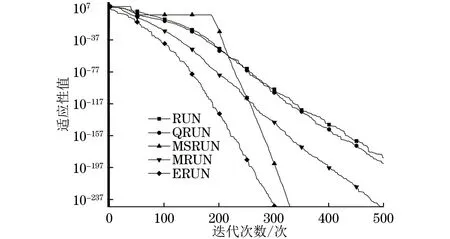
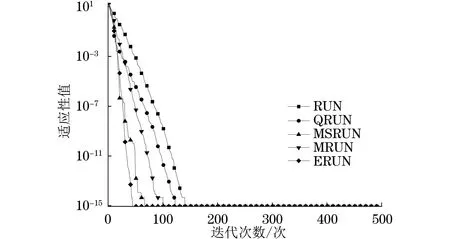
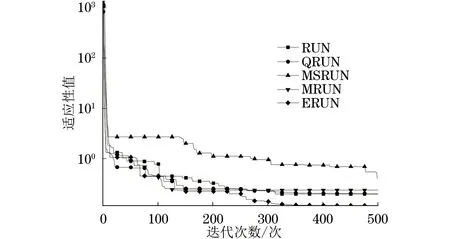
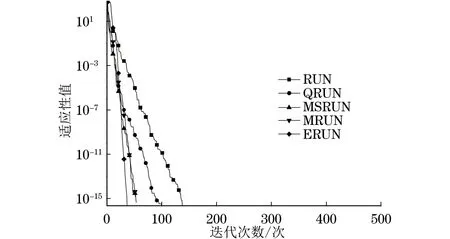
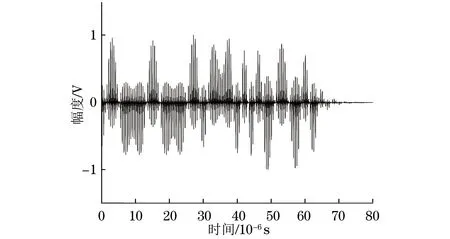
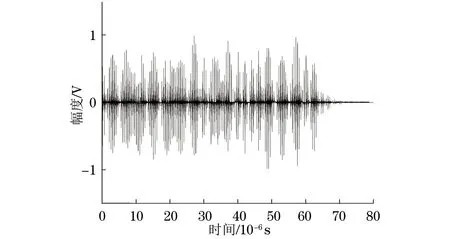
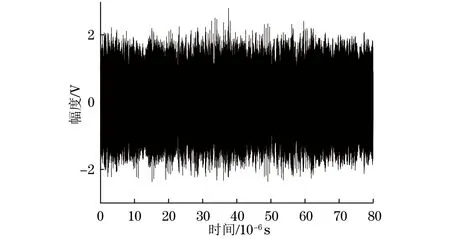
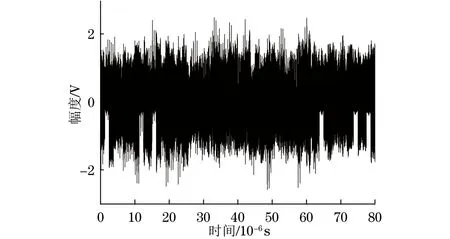
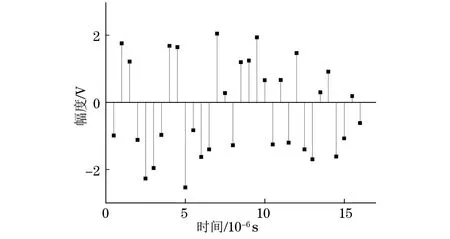
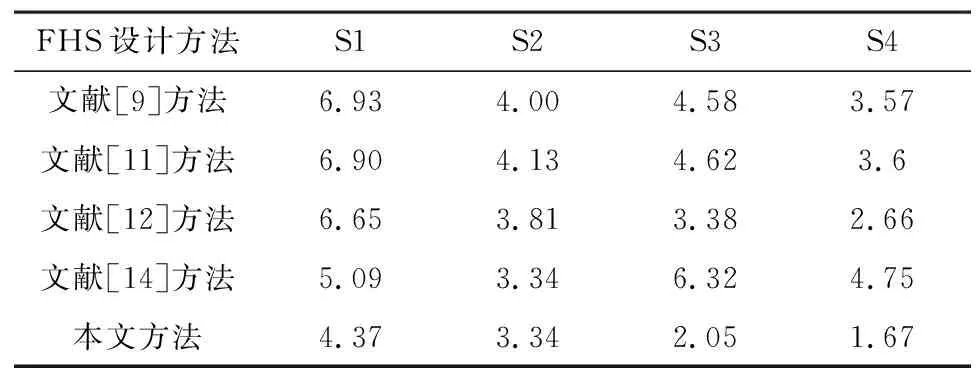
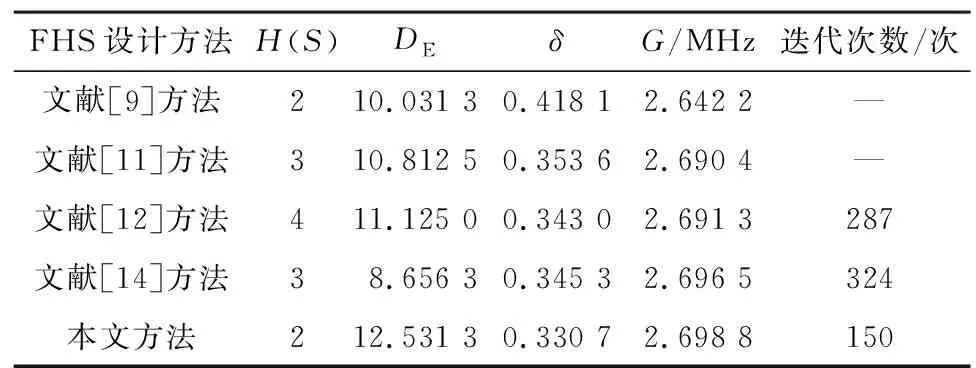
H(S)=max{HS(τ)},1≤τ (5) 在式(4)中,i+τ为模l运算,并且h(si,si+τ)为: (6) 理想的跳频序列应具有尽可能高的复杂度,以提高跳频序列的抗截获能力和破译难度。跳频序列复杂度通常使用模糊熵、近似熵等熵值来度量[16-17]。散布熵[18]作为度量序列复杂度的新方法,具有计算速度快和兼顾幅值间关系的优点。跳频序列S在嵌入维数为m、类数为c、时延为d时的散布熵如下: DE(S,m,c,d)= (7) 其中:p(πv0v1…vm-1)为每种散布模式的概率。本文取m=2、c=4、d=1。 性能良好的跳频序列,各频点在单周期中出现的次数应基本相同,以降低受到干扰的概率。跳频序列的均匀性δ如下: (8) 其中:ni为频点fi在单周期内出现的次数。δ越小,序列的均匀性越好。 平均跳频间隔是指所有相邻2次跳频频率间隔的平均值,跳频序列应具有尽可能大的平均跳频间隔,以提高抗跟踪干扰的能力。跳频序列的平均跳频间隔定义为: (9) 其中:i+1为模l运算。 传统的跳频序列设计方法往往以某单一指标作为设计目标,未考虑各指标间的相互影响,导致跳频序列的各指标之间难以权衡取舍。为兼顾各项指标,本文根据最大汉明自相关性、复杂度、均匀性、平均跳频间隔这4项指标,利用加权法构建目标函数,旨在建立适用于启发式优化算法的跳频序列设计模型。 首先,将各指标转化为最小化指标并归一化: (10) (11) (12) 其中:ΔF=Fmax-Fmin,Fmax与Fmin分别表示频点集中最大频点与最小频点。 构建目标函数为: (13) 模糊层次分析法基于层次分析法,通过添加模糊数学理论对目标指标进行模糊评价,能够降低评价过程中的主观随意性[19]。定义模糊判断矩阵R如表1所示,其中,A1~A4分别表示最大汉明自相关性、复杂度、均匀性与平均跳频间隔这4项指标。 表1 模糊评价判断矩阵Table 1 Fuzzy evaluation judgment matrix 根据模糊层次分析法得到权重ω1、ω2、ω3、ω4,将其代入到目标函数,使用启发式优化算法按目标函数进行寻优即可得到跳频序列。 2.1.1 基于四阶龙格库塔法的个体更新 在个体更新中,RUN基于由四阶龙格库塔法得到的领导搜索因子进行更新,如下: (14) 其中:方向因子r是一个值为1或-1的整数;g是一个[0,2]内的随机数;μ=0.5+0.1randn;randn是一个正态分布的随机数;Xp为勘探领导者;Xm为开发领导者;SF为平衡因子;SM为领导搜索因子。 领导搜索因子SM通过四阶龙格库塔法计算: (15) XRK=k1+2k2+2k3+k4 (16) (17) uXb+rand2k1ΔX) (18) (19) uXb+rand2k3ΔX) (20) 其中:rand1和rand2是[0,1]内的2个随机数;随机参数u=round(1+rand)(1-rand);ΔX为位置增量;Xb为附近最优个体;Xw为附近最差个体。 位置增量ΔX如下: ΔX=2rand|Step| (21) Step=rand(Xb-randXavg+γ) (22) (23) 其中:Step为步长参数;Xavg为全部个体的平均;ub、lb为搜索上限和下限;i为当前迭代次数;iMax为最大迭代次数。 假设搜索问题为最小化问题,Xb和Xw可通过如下逻辑确定: iff(Xn) Xb=Xn Xw=Xbi else Xb=Xbi Xw=Xn end (24) 其中:f(Xn)和f(Xbi)分别为Xn和Xbi的适应度值;Xbi为3个随机个体XA、XB、XC中的最优个体。 领导者如下: Xp=φXn+(1-φ)XA (25) Xm=φXbest+(1-φ)Xlbest (26) 其中:φ是一个[0,1]内的随机数;Xbest是迄今为止的最优个体,Xlbest是该次迭代最优个体。 平衡因子SF如下: (27) 其中:p和q为控制参数。 2.1.2 个体质量增强(ESQ) 为了提高个体质量,防止算法陷入局部最优,RUN使用个体质量增强对更新后的个体进行质量增强: ifrand<0.5 ifω<1 Xnew2=Xnew1+ r′ω|(Xnew1-X′avg)+randn| else Xnew2=(Xnew1-X′avg)+ end end (28) (29) (30) Xnew1=φX′avg+(1-φ)Xbest (31) 其中:r′为取值为1、0或-1的随机数;φ为[0,1]内的随机数;g=5rand;α和u′为[0,2]内的随机数。 若无法产生更好的个体,即f(Xnew2)>f(Xn),则再进行一次新的个体创建,如下所示: ifrand<ω Xnew3=Xnew2-randXnew2+ SF(randXRK+vXb-Xnew2) end (32) 其中:v=2rand。 2.2.1 混沌反向学习机制 由于RUN是随机创建初始种群的,若初始种群的搜索范围过小,会降低算法的收敛速度和稳定性。反向学习机制(OBL)[20]能够提高初始个体的质量,加快收敛速度。然而,随机初始个体的反向个体质量不一定够好。因此,提出混沌反向学习机制,先使用Tent混沌映射提高初始个体的多样性,再使用反向学习机制得到质量更好的初始个体。 基于Tent混沌映射能够生成均匀分布搜索空间的初始种群,相较于Logistics混沌映射具有更好的均匀性和更快的迭代速度[21]。Tent序列如下所示: (33) 根据Tent序列在搜索空间中生成初始个体Xi(Xi,1,Xi,2,…,Xi,D): Xi,j=lbj+(ubj-lbj)xj (34) 其中:lbj和ubj分别为第j维的下界与上界,j=1,2,…,D。 经过Tent映射得到的个体,其对应的反向个体X′i为: X′i,j=lbj+ubj-Xi,j (35) 计算初始个体与反向个体的适应度,将其中最优的N个作为初始种群,从而提高初始种群的质量。 2.2.2 二次插值法 二次插值法是一种局部开发方法,其基本思想是在搜索区域中用3个已知点去拟合一条二次曲线,基于二次曲线极值点来获得近似函数最优解。目前,二次插值法已被应用于黑寡妇蜘蛛优化算法[22]、正弦余弦算法[23]等算法的改进中,能够有效提高收敛速度和寻优精度。 RUN个体更新中最关键的是斜率的计算,而Xbi决定了斜率的方向。因此,将产生Xbi的XA(a1,a2,…,aD)、XB(b1,b2,…,bD)、XC(c1,c2,…,cD)作为参与二次插值的3个点,基于二次插值法得到改进个体: (36) 其中:i=1,2,…,D。 利用改进个体X′bi来确定Xb和Xw,使得SM有更优的前进方向,从而提高算法的收敛速度和寻优精度。 2.2.3 自适应t分布扰动 个体进行强化的概率是固定的,对不同个体的针对性不足,容易出现无效扰动。本文采用自适应t分布对个体进行扰动,并基于个体适应度采取不同的扰动策略。 t分布又称学生分布,其曲线形态与自由度参数m有关:当m=1时,t分布为柯西分布;当m为无穷大时,t分布为高斯分布,如图1所示。 图1 不同分布的概率密度曲线Fig.1 Probability density curves of different distributions 对于个体Xn,基于自适应t分布的扰动如下: X′n=Xn+Xnt(iter) (37) 其中:X′n为扰动后个体;t(iter)为以迭代次数iter为自由度的t分布。在迭代前期,t分布近似柯西分布,其概率密度在0处的峰值较小,因此对个体的扰动较为强烈,能够帮助个体跳出局部最优;在迭代后期,t分布近似高斯分布,其概率密度在0处的峰值较大,因此对个体的扰动较为平缓,能够帮助个体快速收敛。 对扰动后个体基于贪婪原则进行选择: (38) 为提高扰动针对性,基于个体适应度对个体扰动做出区分。若个体适应度比种群平均适应度低,说明该个体具备搜索潜力,对其进行自适应t分布扰动,以便个体在其附近跳动;若个体适应度比种群平均适应度高,说明该个体不具备搜索潜力,对其进行质量增强,以便在搜索空间生成新个体。个体的扰动策略可表示为: (39) 2.2.4 时间复杂度分析 设种群规模为N、维度为D、最大迭代次数为M。RUN主要包括初始化、个体更新、个体质量增强步骤,时间复杂度为TRUN=O(2N+2N2+M×(3N+N2+32))。在ERUN中:初始化时间复杂度为T1=O(4N+4N2);在个体更新阶段,基于二次插值法得到新个体并计算其适应度,再进行个体更新,时间复杂度为T2=O(M×(3N+N2));在扰动阶段,自适应t分布扰动与ESQ时间复杂度一致,T3=O(M×2N)。因此,ERUN总的复杂度为TERUN=O(4N+4N2+M×(5N+N2))。可见,ERUN的时间复杂度在数量级上与RUN保持一致。 一般情况下,频点由跳频系统的工作带宽和跳频间隔决定,使用跳频间隔对整个工作带宽进行划分,得到多个区间,即窄带,每个窄带对应一个频点。在ERUN中,种群个体与跳频序列一一对应,在个体更新时使用连续变量,在计算适应度时将连续变量根据对应的区间转化为频点。 基于ERUN的跳频序列设计流程如图2所示,执行步骤如下: 图2 基于ERUN的跳频序列设计流程Fig.2 Frequency-hopping sequence design process based on ERUN 输入跳频系统工作带宽fmin~fmax,跳频系统频点集F={f0,f1,…,fq-1},跳频序列长度l 输出跳频序列 步骤1初始化种群数量N、最大迭代次数Maxit。令维度D=l,下限lb=fmin,上限ub=fmax,将[lb,ub]划分为q个区间,分别对应q个频点。 步骤2利用Tent混沌映射得到N个个体,根据反向学习得到对应的反向个体。计算所有个体的适应度,选取最优的N个作为初始种群。 步骤3随机选择3个个体,根据式(36)得到改进个体X′bi,进而得到SM,根据式(14)更新个体位置。 步骤4计算当前种群平均适应度,根据式(39)对个体进行自适应t分布扰动或ESQ。 步骤5判断迭代次数是否达到最大迭代次数,若满足要求,则执行步骤6,否则返回步骤3。 步骤6根据最优个体得到跳频序列。 为了验证ERUN的寻优性能,选取文献[15]中的部分测试函数,包括3个单峰函数f1、f3、f5和3个多峰函数f10、f12、f13。开发环境为Matlab 2020b,运行环境为Windows 10(64位)操作系统,CPU为Intel®CoreTMi7-9750H,主频为2.6 GHz,计算机内存大小为16 GB。 选择RUN、量子龙格库塔优化算法(QRUN)[24]、结合黏菌学习的龙格库塔优化算法(MSRUN)[25]、改进龙格库塔优化算法(MRUN)[26]、ERUN进行测试。各优化算法的参数同原文,种群规模为30,迭代次数为500次,重复30次实验,统计最优值、均值与标准差,如表2所示,收敛曲线如图3~图8所示。 图3 f1收敛曲线对比Fig.3 Comparison of f1 convergence curves 图4 f3收敛曲线对比Fig.4 Comparison of f3 convergence curves 图5 f5收敛曲线对比Fig.5 Comparison of f5 convergence curves 图6 f10收敛曲线对比Fig.6 Comparison of f10 convergence curves 图7 f12收敛曲线对比Fig.7 Comparison of f12 convergence curves 图8 f13收敛曲线对比Fig.8 Comparison of f13 convergence curves 表2 测试函数优化结果Table 2 Test function optimization results 在单峰函数上,ERUN在f1、f3、f5上均能稳定收敛到最优值,且相较于MSRUN,ERUN收敛曲线更为合理,收敛速度更快;在多峰函数上,ERUN在f12上寻优精度更好,在f10、f13上与其他算法寻优精度相同,但收敛速度更快。综上所述,在同样的测试环境下,ERUN相较于RUN及其3种变体,具有更高的寻优精度和更快的收敛速度。 在某军用跳频通信设备中,信息脉冲共32位,脉宽为0.5 μs,采样频率为200 MHz,上采样倍数为100倍。在滚降滤波器中,码元速率为0.5 MHz,基带滤波采样速率为2 MHz,滚降参数R=0.22。跳频系统1个码元调频2次,故跳频序列长度为64。跳频范围为3~35 MHz,跳频间隔为1 MHz,故划分为32个频点。过程分析中的干扰以阻塞式调幅干扰为例。 根据目标函数进行寻优,定义种群规模为30,最大迭代次数为500次,收敛曲线如图9所示。可见,相较于其他算法,ERUN在目标函数上具有更高的寻优精度,且在150次迭代时基本收敛,具有较快的收敛速度。 图9 目标函数收敛曲线对比Fig.9 Comparison of objective function convergence curves 在发送端,首先将数字信号调制为双极性信号,如图10所示;然后进行上采样,使用根升余弦滚降滤波进行脉冲成型,如图11所示;最后按照ERUN得到的最优跳频序列进行载频,作为发射信号,如图12所示。 图10 双极性信号Fig.10 Bipolar signal 图11 经脉冲成型后的信号波形Fig.11 Signal waveform after pulse-shaping 图12 经跳频后的信号波形Fig.12 Signal waveform after frequency hopping 在接收端,首先从信道中接收到受干扰信号,如图13所示,可见信号受干扰严重,干扰信号已完全覆盖发送信号;然后对接收信号按照相同跳频序列进行混频解跳,如图14所示,由于干扰频率与序列中的频点不对应,因此解跳后信号中的干扰被抑制,幅度发生变化;最后将解跳信号进行匹配滤波,再进行下采样,如图15所示,匹配滤波后的双极性信号虽然幅度发生了改变,但可以通过正负关系得到数字信号,实现数据的正常接收。 图13 接收信号波形Fig.13 Received signal waveform 图14 经解跳后的信号波形Fig.14 Signal waveform after de-hopping 图15 经匹配滤波后的接收信号Fig.15 Received signal after matched filtering 综上所述,本文方法设计的跳频序列能够在跳频系统中有效应用。 设定发送次数均为20 000次,干扰信噪比均为-6 dB,建立多种干扰环境,包括:S1(调幅调频干扰),S2(调相干扰),S3(前半段为调幅干扰,后半段为调频干扰),S4(前半段为调幅干扰,后半段为调相干扰)。计算不同跳频序列在不同干扰环境中的误码率,如表3所示。可以看出:文献[9]方法仅考虑汉明相关性,误码率较高;文献[11]方法以提升复杂度为目标,误码率较文献[9]方法没有明显差别;文献[12]方法使用混沌系统,跳频序列的误码率较传统方法高,但差距不大;文献[14]方法在干扰不变时展现出了较强的抗干扰能力,但由于其目标函数是针对固定干扰的,干扰类型一旦变化,误码率就会大幅上升;本文方法不仅在固定干扰环境中具有较低误码率,而且在干扰变化的环境中仍保持了较低误码率,展现出了在不同干扰环境下较强的抗干扰能力。 表3 不同跳频序列在多种干扰环境下的误码率Table 3 The bit error rate of different frequency hopping sequences in various jamming environments % 为详细分析不同设计方法的跳频序列性能和寻优速度,选择文献[9,11-12,14]中的设计方法进行对比,跳频系统参数同上文,优化算法最大迭代次数为500次,共有参数保持一致。计算各跳频序列的最大汉明自相关性、散布熵、均匀性、平均跳频间隔和基本收敛时的迭代次数,如表4所示。根据Lempel-Greenberger界[27],跳频序列的汉明自相关性值下界为2。文献[9]方法跳频序列基于抽取m序列设计,能够使汉明自相关性值达到下界,但在其他参数上没有进行优化;文献[11]方法基于改进祖冲之算法,跳频序列汉明相关性和复杂度较好,但均匀性和跳频间隔较差;文献[12]方法跳频序列以优化复杂度为目标,因此复杂度较优,但其他各项指标较差;文献[14]跳频序列虽然均匀性和平均跳频间隔较好,但复杂度较差,且收敛速度较慢;相较于其他设计方法,本文设计的跳频序列最大汉明自相关性值能够达到下界,具有更好的性能指标和较快的收敛速度。 表4 不同跳频序列的评价指标Table 4 Evaluation indices for different frequency hopping sequences 本文对跳频序列的设计问题进行了深入研究。首先,提出利用汉明相关性、复杂度、均匀性、平均跳频间隔作为评价指标,构建目标函数,建立跳频序列优化模型。然后,引入龙格库塔优化算法,基于混沌反向学习机制、二次插值法和自适应t分布扰动,提出增强型龙格库塔优化算法。改进后的算法相较于RUN的几个最新变体,在测试函数和实际问题上具有优势。最后,利用增强型龙格库塔优化算法对跳频序列模型进行优化,将得到的跳频序列用于跳频抗干扰中,取得了较好的效果。随着未来启发式优化算法性能的进一步提升,可在跳频序列设计模型中加入更多性能指标,以提高跳频系统在复杂干扰环境下的抗干扰能力。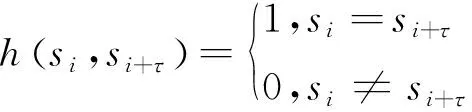
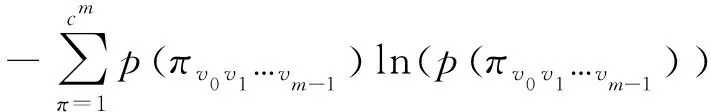


1.3 跳频序列设计模型
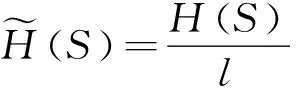




2 基于增强型龙格库塔优化算法的跳频序列设计
2.1 龙格库塔优化算法
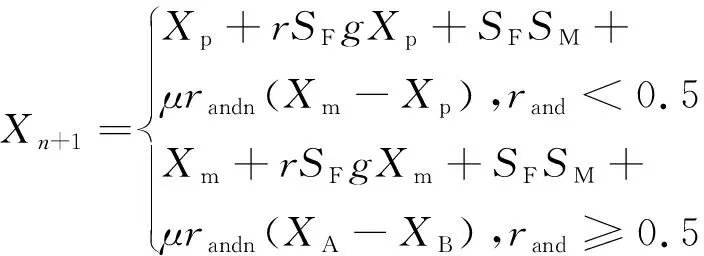

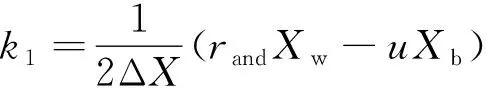



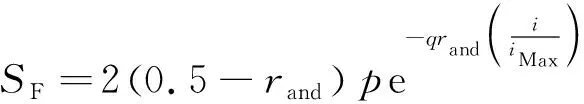

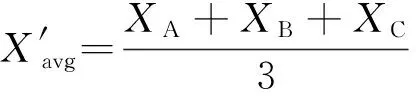
2.2 增强型龙格库塔优化算法
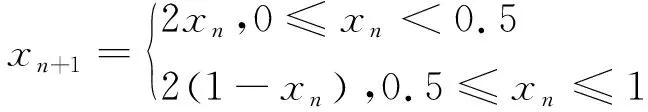
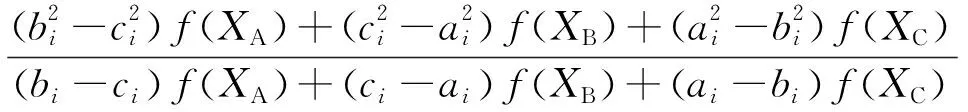
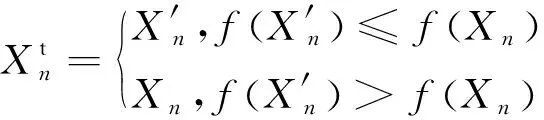
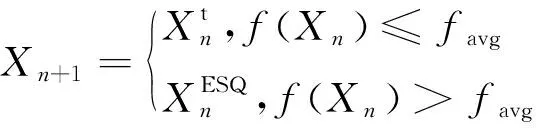
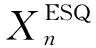
2.3 基于ERUN的跳频序列设计流程
3 实验分析
3.1 ERUN性能测试


3.2 跳频过程分析


3.3 抗干扰效果对比
3.4 跳频序列性能分析
4 结束语

