基于特征对比学习和图卷积的社交网络用户分类

李政学,李枝名,彭德中,陈杰

(四川大学计算机学院,四川 成都 610065)

0 引言

社交网络是一种基于互联网的以人类社交为核心的网络服务形式。随着移动设备的普及和互联网技术的不断发展,社交网络在人类生活中占据了重要地位[1]。人们可以通过社交网络平台上传图片、音频等,也可以与社交网络上的其他用户分享感兴趣的话题[2]。由于社交网络的开放性和连接性,许多企业家也会通过社交网络进行商业活动[3]。在这些社交网络平台中,了解用户的兴趣爱好、发现他们擅长的领域,然后将兴趣相同的人互相推荐为好友或者给他们推荐类似的产品,这些都可以提升社交网络平台的用户体验[4]。由于确定用户的爱好专长是社交网络中的用户分类任务,因此用户分类一直是社交网络的研究热点之一。

社交网络平台通常包括以下功能:用户分享与自己兴趣爱好相关的内容,社交平台针对内容的性质创建对应的社区,用户根据自己的喜好关注不同的社区,用户订阅其他用户发布的内容。因此,用户分享的内容是用户的属性之一,用户根据他们的兴趣爱好加入相应的社区。社交网络用户分类即通过用户自身的属性、关注关系,预测出他们的兴趣爱好。例如,一个刚注册的新用户还未加入任何社区,但他关注了另一个老用户,社交平台发现老用户加入了旅行社区,并且新老用户发表了单车相关的内容,于是平台预测新用户的爱好是单车旅行,便可以邀请他加入旅行社区或者推荐相关的产品,这样便可以提高用户的满意度。

在社交网络中的每个用户都可以视为一个节点,用户之间的关系可以视为节点之间的边,因此社交网络中的用户分类即可视为图中的节点分类[5]。由用户和用户之间的关系构成的社交网络数据结构是一个典型的图数据结构,如何有效地利用节点的属性信息以及网络的结构信息对节点进行分类是一个关键的问题。另外,在社交网络用户分类的应用场景中,图类数据集具有低同质率的特点。图中的同质性指的是任意2个相邻节点的相似性,即如果它们的标签相同,则2个节点相似[6]。同质率是标签相同的邻居节点对占所有邻居节点对的比例,同质率的高低决定了图是同质的还是异质的。

基于随机游走的方法在对图类数据进行节点分类时取得了较好的效果[7]。PEROZZI等[8]提出的DeepWalk是一种学习网络中节点隐表达式的算法,首先通过随机游走获取网络中的节点序列,然后利用Word2Vec的思想将节点变为低维向量[9],最后用于分类。但是,DeepWalk存在以下不足:1)仅利用了图的结构信息,但没有使用节点的属性信息;2)游走是一种均匀的游走,不适合处理同质率较低的图数据集。为了解决DeepWalk只能随机采样的缺陷,GROVER等[10]提出在随机游走时采用有偏策略的Node2Vec,通过p、q2个超参数来控制访问节点的顺序是偏向于深度优先还是广度优先。该方法虽然能够在一定程度上控制随机游走的有偏性,但仍然存在没有利用节点自身属性信息的缺陷。

图卷积神经网络(GCN)在处理图这类非欧氏数据时具有明显的优势。普通的卷积神经网络(CNN)在处理图像这类欧氏数据时,利用它们的平移不变性,通过卷积核来提取原始数据的特征,但图类数据具有不规则性,所以传统的CNN无法处理这类非欧氏数据。GCN首先通过图上的傅里叶变换和卷积定理定义了谱域上的卷积核,然后通过一阶切比雪夫多项式近似来减少计算量,最后定义了图卷积。GILMER等[11]提出的消息传递神经网络(MPNN)将图神经网络分为消息传递和读出2个阶段。GCN针对节点级的任务主要包括消息传递阶段的聚合邻居和更新状态2个步骤,将得到的信息进行非线性映射,增强模型的表达能力。相比于传统的神经网络只能将节点属性信息作为输入[12],无法有效地处理图类数据的结构信息,GCN的优势在于同时考虑了节点的属性信息和图的结构信息[13]。相比于传统的卷积神经网络,GCN的优势在于能够利用图上的卷积算子对非欧氏的图类数据进行特征提取。

GCN模型将卷积算子扩展到图类数据上[14],使节点分类在同质率高的图数据集中取得了较好的效果。图注意力(GAT)模型通过引入注意力机制[15],能够学习更多的图结构信息,在节点分类任务中取得了更好的效果。但是上述方法都存在只适用于高同质率图数据集的缺陷,在处理低同质率数据集时效果会变差。例如,GCN会将各邻居节点的特征聚合,然后使邻居节点的表达式变得相似。针对低同质率即大多数邻居节点与中心节点都不属于同一类节点的情况,GCN会使异类节点的表达式也变得相似,导致分类效果较差。HE等[16]提出的块建模引导的图卷积神经网络(BMGCN)通过构造块矩阵来有区分地聚合同质图或异质图的特征信息,在处理低同质率数据集时分类效果较好,但是该方法仅是从聚合信息的角度出发,并没有从节点表达式的角度考虑。

对比学习是一种自监督的学习方式[17],在没有标签的情况下,使模型观察数据的相似和差异来学习数据的高级特征。YOU等[18]通过最大化子图的不同增广版本的相似性来学习节点的表达式,但该方法未用节点级的样本进行对比。XU等[19]提出的对比学习模型保证了多视图公共特征的一致性,但多视图的对比并不适用于单视图的图类数据集。

针对社交网络中图类数据集同质率较低的问题,本文提出基于特征对比学习的图卷积神经网络(CLGCN)模型。CLGCN的特征对比学习模块从节点级的样本出发,将同类、异类的邻居节点对分别定义为正、负样本对,通过最小化特征对比的损失函数,使得同类节点的特征相似性更高及异类节点的特征可区分性更强。

1 相关工作

本节介绍图卷积神经网络和对比学习的相关工作以及常见的相似性衡量方法。

1.1 图卷积神经网络

近年来,由于图神经网络模型具有能够有效处理图类数据的优势,因此它在处理图类节点分类任务时也越来越受欢迎。KIPF等[14]在此基础上提出了GCN,将拉普拉斯矩阵特征分解后进行的傅里叶变换定义为了图上的卷积算子,并通过切比雪夫的一阶近似减少了计算量。

经典的GCN处理半监督节点分类任务的过程如式(1)所示:

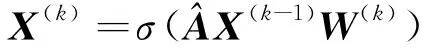
(1)

针对半监督学习的节点分类任务,GCN的最后一层(K)如式(2)所示:

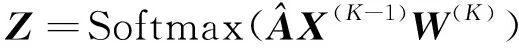
(2)

其中:Z为用于分类的节点表达式。

该节点分类任务采用交叉熵作为损失函数[20],如式(3)所示:

Lgcn=CrossEntropy(Yij,Zij)=

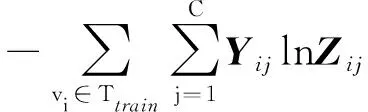
(3)

其中:Y表示训练集的真实标签矩阵;C表示类别的数量。

CLGCN模型受到BMGCN[16]的启发,具体过程如下:

1)通过多层感知机(MLP)获取伪标签,如式(4)所示:

L=Softmax(σ(MLP(X)))

(4)

其中:X表示节点特征。

2)为了增强伪标签的可靠性,该模型用训练集的真实标签先对MLP进行预训练,用交叉熵作为预训练阶段的损失函数,如式(5)所示:

(5)

其中:Ttrain表示训练集中所有节点的集合;Yi表示节点vi的真实标签;Li表示节点vi的伪标签。

3)在得到伪标签L后,将伪标签与真实标签相结合得到Yc和块矩阵M,分别如式(6)和式(7)所示:

Yc={Yi,Lj|∀vi∈Ttrain,∀vj∉Ttrain}

(6)

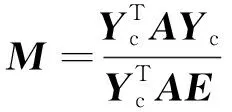
(7)

其中:A是邻接矩阵;E是与Yc形状相同的全1矩阵;块矩阵M反映了任意2个类别之间有边连接的概率。

4)构造块相似性矩阵N,如式(8)所示。N衡量了M中类别之间的相似度,借助N构造新的邻接矩阵,如式(9)所示。利用块矩阵引导图卷积,如式(10)所示。

N=MMT

(8)

(9)

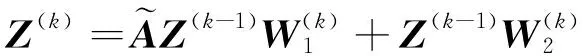
(10)

5)采用交叉熵作为损失函数。损失函数的计算公式如式(11)所示:

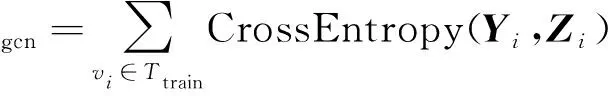
(11)

1.2 对比学习

对比学习在无监督学习中进行特征学习和数据增广时发挥着重要的作用。例如,XU等[19]在多视图聚类的任务中进行特征对比学习,将多视图样本中的任意2个不同视图的相同特征对作为正样本对,将其余的特征对作为负样本对,该方法减少了不同视图冗余信息的干扰,保证了公共特征的一致性。

在半监督学习的节点分类任务中,由于只有有限的数据具有标签,对比学习在图卷积神经网络中也可以发挥更好的作用。例如:VELICKOVIC等[21]提出的深度图信息最大化(DGI)将图中局部和全局的表示式进行对比,丰富了节点的表达;SUN等[22]将DGI扩展到图级别上,对图进行分类;THAKOOR等[23]利用对比学习的思想随机删除图中的边来进行数据增广。

1.3 相似性衡量方法

常见的衡量向量相似性的方法有欧氏距离、集合距离、余弦相似性等。假设有2个向量a=(a1,a2)和b=(b1,b2),则它们之间欧氏距离的计算公式如下:

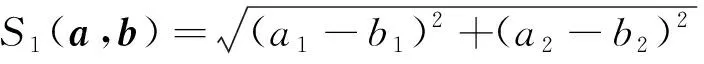
(12)

欧氏距离是用来衡量两点之间的直线距离的方法,它只适用于欧氏数据,并且在数据维度较高时容易造成维度灾难的问题[24],图类数据属于非欧氏数据,因此欧氏距离并不适用。

基于集合距离的方法有Jaccard指数、Dice指数等。Jaccard指数的计算公式如下:

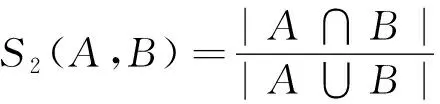
(13)

其中:A、B分别表示2类向量的集合,这类方法适用于衡量集合之间的相似性。

本文是以单个向量为对象,衡量它们两两之间的相似性,因此基于集合距离的方法并不适用。

衡量a=(a1,a2)和b=(b1,b2)之间余弦相似性的计算公式如下:

(14)

其中:〈·,·〉表示内积运算。

余弦相似性是计算向量之间夹角的余弦值,从方向的角度来衡量向量之间的相似性,因此适用于本文中的图类数据。

2 CLGCN模型

本节首先给出社交网络用户分类的问题描述,然后介绍CLGCN模型。

2.1 问题描述

一个社交网络的图可以用G=(V,E,X,A)来表示,其中,V表示社交网络中的节点,即用户集合,E表示节点之间的边,即用户之间的相互关注,X∈n×F表示节点特征向量构成的矩阵,A∈{0,1}n×n表示社交网络中所有节点之间关系的邻接矩阵,n=|V|表示节点的数量,F表示节点特征向量的维度。通常地,将社交网络中的用户分类视为半监督的节点分类问题。在训练集中已知标签的节点集合Ttrain表示已经明确喜好的老用户,对应的标签集合用Y∈n×C表示。在测试集中未知标签的节点集合Ttest表示未明确喜好、刚刚注册的新用户。社交网络用户分类即通过用户之间的关注关系、用户自身属性,预测新用户的兴趣爱好。

2.2 图卷积神经网络模型

CLGCN模型结构如图1所示,主要包括预训练、图卷积和对比学习3个部分:第1个部分先通过预训练获取未知标签节点的伪标签,再将伪标签与真实标签组合;第2个部分先通过结构相似性矩阵构造新的邻接矩阵,再进行图卷积;第3个部分有7个节点,其中,0号节点为中心节点,其余1～6号节点为邻居节点,1号节点与0号节点为同类,其余节点与0号节点为异类,同类节点构成的节点对作为正样本,例如〈v0,v1〉,异类节点构成的节点对作为负样本,例如〈v0,v6〉,以此选取所有的正负样本来构造特征对比学习的损失函数。总的损失函数由3个部分的损失函数组成。

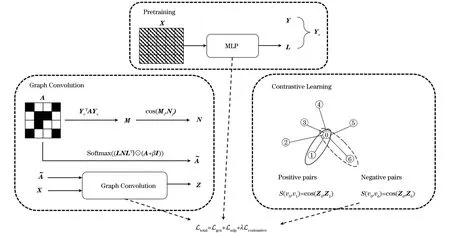
图1 CLGCN模型结构Fig.1 Structure of CLGCN model

2.2.1 基于相似性矩阵的图卷积

1)通过预训练得到的伪标签矩阵L与真实矩阵Y组成组合标签矩阵Yc,如式(15)所示。通过Yc∈n×C可以构造一个块矩阵M∈C×C,M在一定程度上描述了图中各类的结构特征,即M矩阵中每一行的向量表示了该类的结构信息,如式(16)所示。

Yc={Li,Yj|∀vi∉Ttrain,∀vj∈Ttrain}

(15)

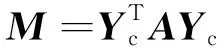
(16)

其中:A∈n×n为邻接矩阵;Mij表示第i类中的节点与第j类中的节点相连的边数。

2)在得到块矩阵M后,由于其每行反映了图中各类的结构信息,于是可以用它构造一个类别相似性矩阵,用于衡量类与类之间结构的相似性,本文采用余弦相似性来衡量图中各类之间的相似度,如式(17)所示:

Nij=|cos(Mi,Mj)|

(17)

类别相似性矩阵N衡量了类与类之间的相似性,同类和结构相似类之间的节点应当传播更多的信息。首先用伪标签L和类别相似性矩阵N计算权重矩阵LNLT,然后用该权重矩阵来构造更完善的新邻接矩阵,新邻接矩阵的作用是指导节点利用自身和邻居的特征信息来更新自身的特征表达。新邻接矩阵的构造方式如式(18)所示:

(18)

其中:β是一个超参数;I∈n×n是一个单位矩阵。

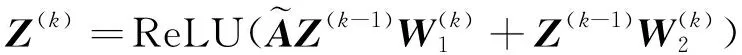
(19)

4)最后一层节点的特征表示如式(20)所示:

(20)

5)图卷积部分的损失函数如式(21)所示:

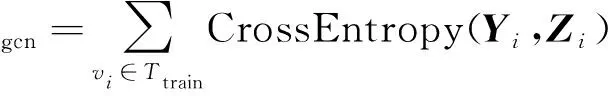
(21)

2.2.2 邻居节点对的特征对比学习

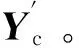
2)将图中每个节点与自身类别相同、不同的邻居节点对分别作为正、负样本对,目的是使同类样本的表达式相似性更高,异类样本的表达式可区分性更强。此处,采用余弦相似性来衡量样本表达式的相似程度,如式(22)所示:

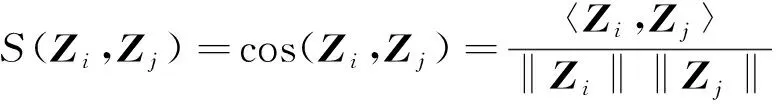
(22)

其中:Zi是节点vi的最终表达式;〈·,·〉是内积运算。

3)定义节点vi的邻居节点对中正样本对的相似性的和如式(23)所示,节点vi的邻居节点对中负样本节点对的相似性的和如式(24)所示。由此得到节点vi的对比学习损失函数如式(25)所示。

(23)

(24)

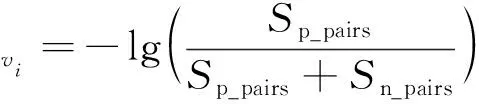
(25)

4)总的对比学习损失函数如式(26)所示,通过最小化损失函数式(26),邻居节点对中正样本对的相似性会更高,负样本对的可区分性会更强。

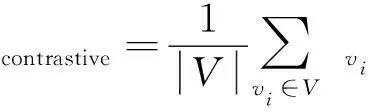
(26)

可见,特征对比学习的引入可以有效减轻社交网络数据集同质率较低的问题对GCN模型的限制。

2.2.3 训练过程

1)通过预训练获取所有节点的伪标签L,此部分的损失函数如式(27)所示:

(27)

2)将伪标签L与真实标签Y相结合得到组合标签Yc。

3)通过组合标签Yc构造衡量类别之间结构相似性的矩阵N。

6)模型总的损失函数如式(28)所示:

Ltotal=Lmlp+Lgcn+λLcontrastive

(28)

其中:λ是人为设定的超参数。

算法1CLGCN模型训练算法

输入特征矩阵X∈n×F,邻接矩阵A∈n×n,标签矩阵Y∈ntrain×C

输出节点表达式Z∈n×C

1) 通过式(15)和式(27)预训练多层感知机获得组合标签Yc。

2) 通过式(16)计算M。

3) 通过式(17)计算相似性矩阵N。

5) 通过式(19)和式(20)进行图卷积。

6) 通过式(22)～式(25)进行正负样本对的特征对比。

7) 通过式(21)、式(26)、式(27)分别计算Lgcn、Lcontrastive、Lmlp。

8) 通过式(28)最小化L更新整个网络的参数。

3 实验结果与分析

将CLGCN模型在3个同质率较低的社交网络数据集上进行节点分类实验,并与其他先进的模型进行性能对比。

3.1 数据集

采用3个公开的社交网络数据集BlogCatalog、Flickr和Uai2010。这3个数据集的信息统计如表1所示。

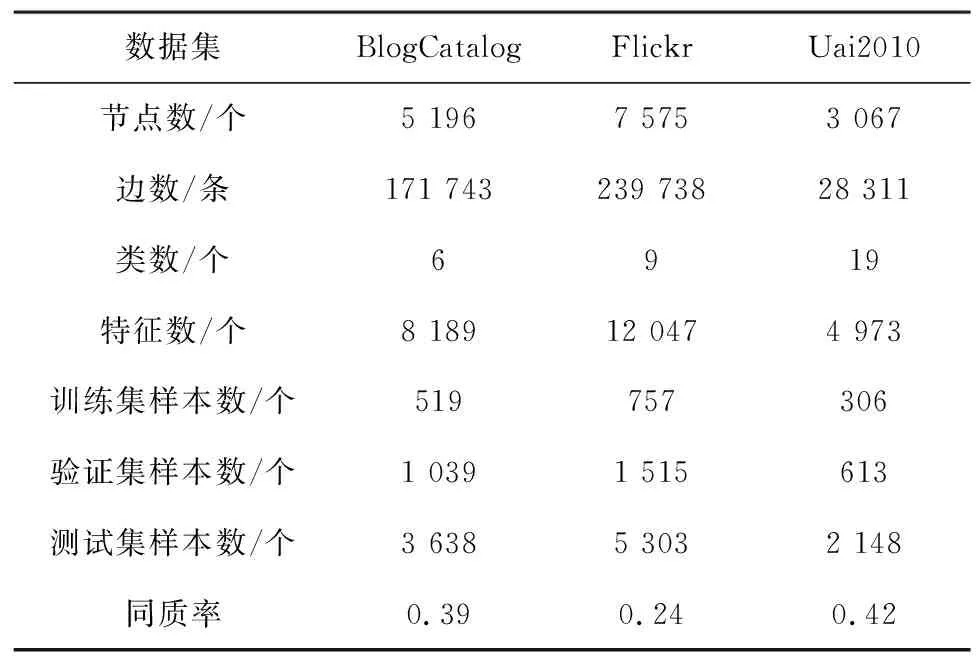
表1 数据集信息统计Table 1 Dataset information statistics

1)BlogCatalog数据集。BlogCatalog是一个在线的社交网络平台,许多用户用它上传博文,并且博主之间可以相互关注,博主之间的关注关系形成了一个社交网络。BlogCatalog数据集用每个用户博客中的关键字作为用户的属性信息,标签来自用户的兴趣爱好,共划分了6类节点。

2)Flickr数据集。Flickr是一个存放图像和视频的网站,用户之间可以通过分享图片和视频来相互交流。Flickr数据集将用户对图片、视频的兴趣爱好的关键字作为属性信息,将用户所在的分组作为标签,共划分了9类节点。

3)Uai2010数据集。Uai2010数据集是一个用于社区检测的网络数据集,共有3 067个节点和28 311条边。

3.2 对比模型

将CLGCN与以下6种先进的用于节点分类的模型进行比较:

1)DeepWalk[8]。该模型是一种随机游走和Word2Vec相结合的模型,通过随机游走获取节点序列,再通过Word2Vec获取向量表达式,仅利用了图的结构信息。

2)GCN[14]。该模型是一种经典的图卷积神经网络模型,将节点的属性信息和网络的结构信息作为输入,通过聚合邻居节点的信息来学习节点的表达式。

3)GAT[15]。该模型将自然语言处理中的注意力机制引入图数据结构,通过计算节点之间边的重要性,使得信息传播更加有效。

4)正交图卷积神经网络(OrthGCN)[25]。该模型是一种用于解决标准GCN过平滑问题而提出的改进模型,利用一种新颖的正交特征变换方式,提升了模型训练过程的稳定性。

5)MixHop[26]。该模型是一种针对标准GCN只能聚合低阶邻居信息而提出的改进模型,通过混合不同阶数邻居节点的特征表达,使传递的信息更加丰富。

6)BMGCN[16]。该模型通过计算图数据集中类别之间的结构相似性来引出块矩阵,然后通过块矩阵引导的图卷积方法能较好地处理低同质率的数据。

3.3 评价指标

实验的主要任务是对图数据集中的节点进行半监督分类,采用准确率作为评价指标。

3.4 实验设置

实验对社交网络数据集进行半监督节点分类,因此数据集分为已知标签的训练集、未知标签的验证集和测试集。BlogCatalog和Flickr数据集采用与GAug[27]中相同的划分,训练集占10%、验证集占20%、测试集占70%。Uai2010数据集来源于AM-GCN[28],也同样按照半监督节点分类的惯例将其划分为训练集占10%、验证集占20%、测试集占70%。

CLGCN模型是在BMGCN上进行修改并且引入特征对比学习得到的改进模型。CLGCN和BMGCN对BlogCatalog数据集进行训练时:共有的隐藏层单元数设置为16、32、64、128、256、512,学习率设置为0.050、0.030、0.010、0.001和丢弃率(dropout)设置为0、0.1、0.2、0.3、0.4、0.5,CLGCN独有的参数λ设置为0、0.1、0.3、0.5、0.7、0.9;对Flickr数据集进行训练时,共有的隐藏层单元数设置为16、32、64、128、256、512,学习率设置为0.001 0、0.000 9、0.000 8、0.000 7、0.000 6、0.000 5、0.000 4、0.000 3、0.000 2、0.000 1和dropout设置为0、0.1、0.2、0.3、0.4、0.5,CLGCN独有的参数λ设置为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0;对Uai2010数据集进行训练时,共有的隐藏层单元数设置为32、64、128、256、512,学习率设置为0.001 0、0.000 9、0.000 7、0.000 5、0.000 3、0.000 1和dropout设置为0、0.1、0.2、0.3、0.4、0.5,CLGCN独有的参数λ设置为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0。其他模型则是在参考原文献中最佳参数的基础上,对学习率、隐藏层单元数、dropout进行微调。

3.5 结果分析

3.5.1 节点分类分析

表2展示了在3个低同质率社交网络数据集上的半监督节点分类的实验结果,其中最优指标值用加粗字体标示,下同。由表2可以看出,CLGCN模型在BlogCatalog、Flickr和Uai2010 3个数据集上的准确率分别达到了93.5%、81.4%和67.9%,高于对比模型,具体表现为:基于随机游走的DeepWalk由于只考虑图类数据的结构信息而忽略了节点的属性信息,因此准确率较低;GCN和GAT同时考虑了图结构信息和节点属性信息,准确率要高于DeepWalk,但存在无法有效处理低同质率数据集的缺陷;MixHop同时聚合了低阶和高阶邻居的特征信息,使学习的特征表达式更加丰富,因此准确率更高,但同样无法有效处理低同质率数据集;BMGCN通过计算出的块矩阵来引导图卷积,能够较好地处理低同质率数据集,准确率要高于GCN、GAT和MixHop;CLGCN将同类邻居节点对作为正样本对、异类邻居节点对作为负样本对及运用特征对比来处理低同质率数据集,在3个数据集上的准确率均高于BMGCN。

表2 社交网络节点分类结果Table 2 Results of the node classification of social networks %

3.5.2 参数分析

在BlogCatalog、Flickr和Uai2010 3个数据集上,分析GCN卷积层数、隐藏层单元数对CLGCN模型性能的影响。

1)GCN卷积层数。在隐藏层单元数、丢弃率、学习率等超参数不变的情况下,测试CLGCN中GCN卷积层数分别为1、2、3、4、5、6的情况下节点分类的准确率,如表3所示。

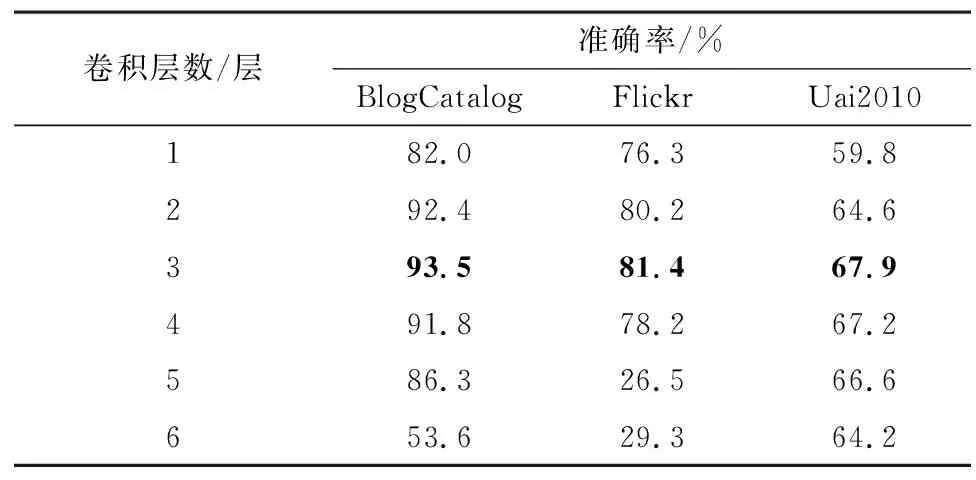
表3 在不同卷积层数下的CLGCN分类结果Table 3 Classification results of CLGCN with different numbers of convolutional layers

由表3可知,随着卷积层数的增加,模型准确率逐渐提升,当卷积层数为3时,模型性能最好,但随着卷积层数继续增加,模型准确率会逐渐变差。这是因为GCN实际上是一个低通滤波器,层数过高会导致过平滑问题。原始GCN模型超过2层性能就会急剧下降,而CLGCN在4层卷积层时仍能保持较好的性能,这是因为特征对比模块使异类节点对的表达特征可区分性更强,在一定程度上缓解了CLGCN中的过平滑问题。

2)隐藏层单元数。在GCN卷积层数、丢弃率、学习率等超参数不变的情况下,测试CLGCN中隐藏层单元数分别为32、64、128、256、512的情况下节点分类准确率,如表4所示。

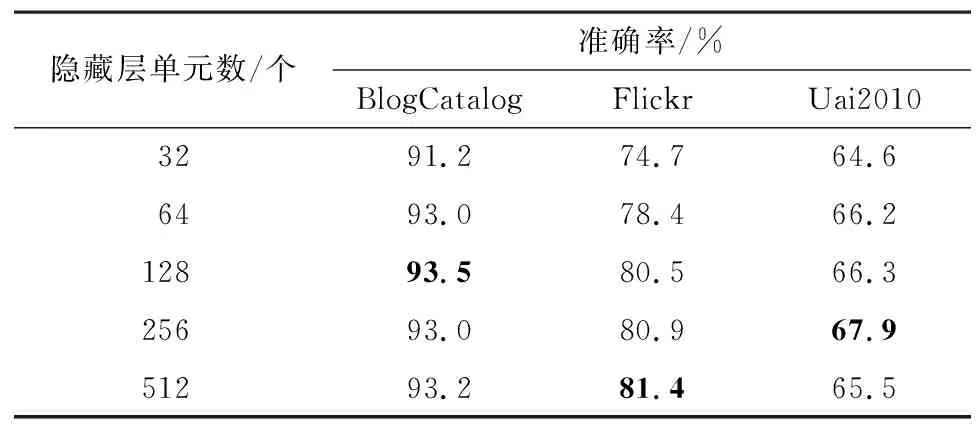
表4 在不同隐藏层单元数下的CLGCN分类结果Table 4 Classification results of CLGCN with different numbers of hidden layer units

由表4可知,当CLGCN隐藏层单元数为128、256、512时,CLGCN的节点分类效果较好,但在其他情况下CLGCN的性能也相对稳定,说明了其对隐藏层单元数有较强的鲁棒性。

3.5.3 可视化分析

为了更直观地展示CLGCN模型的有效性,以同质率最低的Flick数据集为例,用t-SNE对GAT、BMGCN和CLGCN最后一层输出的节点表达式进行可视化。Flick数据集共分为9类,其节点分类的可视化结果如图2所示,其中不同颜色和样式的点表示不同标签的节点。

图2 在Flickr数据集上节点分类的可视化结果Fig.2 Visualization results of node classification on Flickr datasets

由图2的可视化结果可知:GAT由于无法有效处理低同质率的数据集,因此许多不同标签的节点都混合在一起;BMGCN通过块矩阵引导图卷积,能在一定程度上处理低同质率的数据集,可视化结果要比GAT好很多;CLGCN的特征对比学习模块能够从样本表达式的角度有效处理低同质率的数据集,因此可视化结果中可以清楚地看出节点分为9类,且其同类节点的分布更加密集。可见,CLGCN的可视化结果进一步证明了特征对比学习模块的有效性。

3.5.4 消融实验

为了进一步地验证CLGCN特征对比学习模块在低同质率数据集中节点分类的有效性,进行消融实验。将去掉特征对比学习模块的CLGCN用CLGCN*表示,将CLGCN*和CLGCN在所有数据集上进行比较,结果如表5所示。

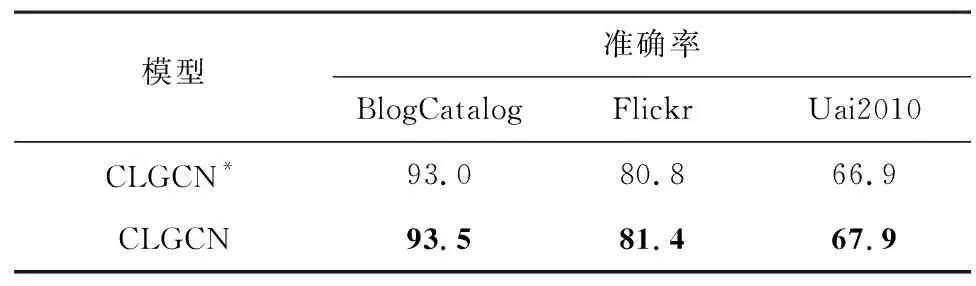
表5 对比学习模块的消融实验结果Table 5 Ablation experimental results of contrastive learning module %

消融实验结果显示,有特征对比学习模块的CLGCN在3个数据集上的准确率均高于没有特征对比学习模块的CLGCN*。CLGCN的特征对比学习模块从样本表达式的角度构造特征的对比损失函数,使同类邻居节点对的特征表达相似性更高及异类邻居节点对的特征表达可区分性更强,最终在处理低同质率数据集时节点分类的效果更好。该实验证明了特征对比学习模块的有效性。

3.5.5 相似性衡量方法对比

该实验对样本表达式的相似性衡量方法进行对比。由于基于集合的距离衡量方式不能较好地满足本文的要求,因此对余弦相似性和欧氏距离2种衡量方法进行比较。

表6展示了相似性衡量方法的对比结果,在3个数据集上,基于余弦相似性的实验结果远好于基于欧氏距离的实验结果,主要原因为:1)社交网络的图类数据属于非欧氏数据,欧氏距离无法有效衡量图类数据;2)在面对高维数据时,由于维度灾难的原因,因此欧氏距离的测度会失去意义。可见,针对社交网络数据集非欧氏及高维的特性,余弦相似性比欧氏距离更加合适。

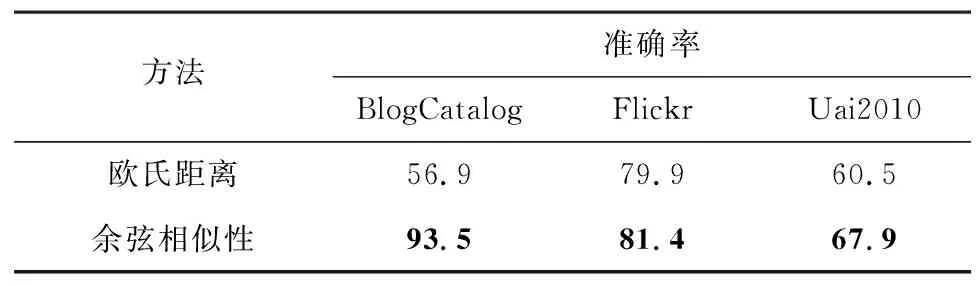
表6 相似性衡量方法的对比结果Table 6 Comparison results of similarity measurement methods %

4 结束语

针对社交网络数据集的低同质率问题,本文提出一种基于特征对比学习的CLGCN模型,通过定义同类节点对为正样本对、异类节点对为负样本对,最小化特征对比的损失函数,使得同类节点特征的相似性更高、异类节点特征的可区分性更强。实验结果表明,CLGCN在社交网络用户分类时相比于其他模型效果更好。但由于不同的社交网络数据集涉及的用户自身属性有所不同,因此未来将考虑根据不同情况采用不同的方法来衡量节点特征的相似性。