求解时间依赖型绿色车辆路径问题的算法研究
葛非,闵珊,邱含,代振阳,杨智敏
(华中师范大学计算机学院,湖北 武汉 430079)
0 引言
物流运输行业作为商品供应链管理的重要环节,成了不同地区经济发展的重要纽带,随着其市场规模的不断扩张,发挥着越来越重要的作用。随着绿色环保理念的普及,公众对交通运输中温室气体排放问题的关注度日益提升。然而,物流企业在追求成本降低和效率提升的过程中,往往忽视了运营活动对环境的影响,尤其是碳和氮氧化物排放,这些温室气体不仅加剧了全球气候变化,还对人类健康和生态系统构成了威胁。自2009年哥本哈根世界气候大会以来,低碳环保和节能减排已成了全球关注的重点,我国政府和相关部门采取了多项措施,包括控制企业排放、实施碳税政策和建立企业碳排放交易系统,以减少运输行业的碳排放。公路运输是我国主要的温室气体排放源之一,碳排放量占交通运输行业总排放量的80%以上。因此,推动燃油汽车的节能降碳是实现“双碳”目标的关键环节[1]。在城市配送中,车辆的燃料消耗和二氧化碳排放与城市每天的交通拥堵情况紧密相关,拥堵的路况会使车辆的油耗量和碳排放量增加,间接对运输过程中的经济成本和环境成本产生负面影响。城市交通拥堵是市区交通碳排放快速增长的关键原因[2]。此外,交通拥堵也会导致车辆配送时间延长,致使车辆不能在客户规定时间窗口内按时到达客户点完成配送任务。因此,研究基于时变交通网络的绿色物流模式,对于适应当前的运输需求和减少环境影响具有重要意义。
绿色车辆路径问题(GVRP)是一个新兴的研究领域,定义为:在满足客户服务要求、车辆容量等约束条件的前提下,将降低运作成本、减少能耗和碳排放、提供顾客满意的服务等作为优化目标,科学规划发车数量、发车时间与车辆行驶路线,实现经济效益、环境效益和社会效益的协调优化[3]。作为基本车辆路径问题(VRP)的扩展,GVRP同样被归类为非确定性多项式(NP)-Hard问题。在国际上,对于GVRP的研究已经取得了显著成果。BEKTAS等[4]提出污染路径问题(PRP),该问题综合考虑了行驶路程、温室气体排放以及行驶时间成本,主要目的是减少车辆行驶过程中的燃油消耗,并建立了带时间窗和不带时间窗PRP的混合整数数学模型,同时采用综合模式排放模型(CMEM)[5]计算燃油消耗量。在BEKTAS等[4]的研究基础上,DEMIR等[6]回顾和比较了几种常见的与公路货运燃料消耗和温室气体排放相关的排放模型,并将模型结果与实际道路数据进行了比较分析。DEMIR等[7]提出一种自适应大规模邻域搜索(LNS)算法求解PRP,该算法通过使用新的和现有的删除和插入策略来优化自适应大规模邻域搜索算法,从而提高求解质量,并通过大量实验验证了该算法的有效性。MEHLAWAT等[8]提出一种混合遗传算法用于解决多车辆GVRP问题,并通过实验验证了该算法的鲁棒性。
虽然已有研究对GVRP问题进行了一系列探讨,但多数研究未充分考虑交通拥堵的影响。文献[5]研究表明:二氧化碳(CO2)排放量与燃料消耗量成正比,且这一关系受车辆行驶速度的影响,严重堵塞将伴随着频繁的加速和减速动作,这将极大增加温室气体的排放量。若在求解绿色车辆路径优化问题时假设车辆速度恒定,这可能导致车辆的日均CO2排放偏离率高达20%,在严重拥挤的交通中偏离率更高[9]。因此,在研究车辆行驶过程中的碳排放量时,考虑交通拥堵能让计算结果更加准确,也更符合实际情况。FRANCESCHETTI等[10]提出时间依赖型污染路径问题(TDPRP),考虑交通拥堵场景对PRP进行扩展,并对TDPRP的整数线性规划公式进行详细描述,并假设车辆速度在一组离散值之间进行优化。CIMEN等[11]考虑在时变路网中车辆速度的时间依赖性和随机性,提出一种基于近似动态规划的启发式算法来解决时间依赖型绿色车辆路径问题(TDGVRP)。KAZEMIAN等[12]将温室气体排放和燃料消耗作为TDGVRP优化目标,并通过将带时间窗的问题转化为不带时间窗的问题来降低求解复杂性,在减少碳排放和油耗的同时控制总成本。
考虑载重和时变路网的TDGVRP研究在最近几年才获得较多的关注,国内就此展开的研究较少。赵志学等[13]研究了考虑不同拥堵情况下的GVRP,将车辆管理使用费用和油耗碳排放成本作为优化目标,并根据模型的特点将模拟退火算法和差分进化算法相结合对GVRP进行求解,实验结果证明该算法能有效减少运输成本以及碳排放成本。周鲜成等[14]考虑车辆不同出发时刻对行驶时间的影响,针对TDGVRP模型的特点,设计基于路段划分策略的车辆行驶时间计算方法,并利用改进的蚁群算法进行求解。珠兰等[15]将包括油耗成本在内的运输总成本作为TDGVRP的优化目标,提出嵌套遗传算法对其进行求解。QI等[16]利用基于Q学习的多目标进化算法(QMOEA)来求解带时间窗的时间依赖型绿色车辆路径问题(TDGVRPTW),在QMOEA中设计1种混合生成初始解的方法和2种基于Pareto前沿的交叉策略以提高算法的求解性能,最后将一个实际物流系统作为实验案例,验证了该算法的有效性和优越性。
对于GVRP的研究,多数文献使用元启发式和启发式算法进行求解,因为精确解法通常仅适用于小规模问题。在GVRP的最新研究成果中,相当一部分内容聚焦于单目标优化,这是因为与双目标问题相比,单目标优化在简化问题和寻找全局最优解方面更具优势,然而多目标优化考虑了更多因素和需求,能够提供多样化的解决方案。多数文献假设GVRP中车辆的行驶速度恒定,只有少数文献考虑了城市路网中时变速度下的碳排放量计算。因此,在时变路网中的双目标TDGVRPTW仍有很大的研究空间。
本文通过加入邻域算子、优化信息素更新方式和状态转移规则等手段对蚁群算法进行了改进,设计了绿色智能进化蚁群优化(G-IEACO)算法,以更好地求解双目标TDGVRPTW。
1 问题描述与模型建立
1.1 问题描述
在TDGVRPTW中,考虑以下核心假设:首先,配送中心拥有数量固定、规格相同的车辆用于物流配送;然后,每个客户点的配送需求包括地理位置、货物需求量、服务时间等,这些信息彼此独立且已知,同时每辆车在最大载货量的约束下可服务多个客户点,但每个客户点只能由一辆车提供服务;最后,所有车辆均从配送中心出发并在完成配送后返回原点,同时所有客户点和配送中心均有时间窗的限制,车辆须在规定的时间窗内为其服务,若提前到达则须等到客户的最早服务时间才能开始服务,若超过时间窗则不能服务客户。
TDGVRPTW的目标是在城市交通条件变化的情况下,车辆安排要最小化碳排放量和总行驶时间。碳排放量与车辆的行驶速度和载重密切相关[17],因此在求解时须考虑实时交通状况。已有研究在求解车辆行驶过程中的碳排放量时忽略了交通拥堵和假设行驶速度恒定,不符合实际情况。在时变交通下,一个工作日被划分为多个时段M={[b1,e1],[b2,e2],…,[bk,ek],…,[bm,em]},其中,bk和ek分别表示周期k的开始时间和结束时间,且e(i-1)=bi,∀i∈{2,3,…,m}。在任一个路径(i,j)上的每一个周期的行驶速度(vijm,∀m∈M)是已知的且每一个周期的行驶速度在该时段内是不变的。TDGVRPTW需要在考虑城市道路拥堵的情况下安排车辆服务完所有客户,并以最小化碳排放量和车辆总行驶时间为目标函数,给出配送方案。
1.2 符号说明
参数和决策变量定义如表1所示。

表1 符号定义Table 1 Symbol definition
1.3 车辆碳排放的计算方法
根据文献[4]可知:车辆的碳排放量与燃油消耗量成正比,可以用CO2转换因子将汽车的油耗量转化为碳排放量,故可以先利用车辆和道路的有关参数求得消耗的燃油量,再计算出车辆的碳排放量。DEMIR等[18]分析了影响燃料消耗的因素,并调查现有的车辆排放模型和回顾绿色道路货运的相关文献,并对多种已有的油耗模型进行了详细介绍,其中提到的CMEM如今被广泛使用在GVRP中。CMEM由BARTH等[19]提出,由发动机功率、发动机转速和燃油率3个部分组成,基于微观的角度,以车辆的瞬时油耗和状态参数之间的关系为推导依据,通过车辆的发动机运行状态参数逐秒计算燃油排放,可以准确计算车辆的油耗,被用于估算车辆行驶过程中的燃料消耗量和CO2排放量[4,6,10]。根据该模型,总燃油消耗量F的计算公式如下:
F=RFR·T=
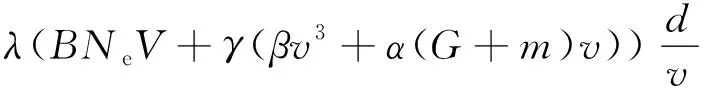
(1)
其中:RFR为瞬时燃油率;T为行驶时间;α=gsinθ+gCrcosθ,g为重力常数,Cr为地面摩擦阻力系数,θ为道路坡度;β=0.5CdAρ,Cd为空气阻力系数,A为车辆迎风面积,ρ是空气密度;γ=1/(1 000εω),ε是车辆传动系统效率,ω是柴油发动机的效率参数;λ=ξ/κΨ,ξ是燃料与空气质量比,κ是经典柴油热值,Ψ是转换因子;B是发动机摩擦因子;Ne是发动机转速;V为发动机排量;G为车辆整备质量;m为货物重量;d为车辆行驶路程;v为车辆行驶速度。
1.4 时段划分方式
MALANDRAKI等[20]通过模拟交通路网中的偶发性交通事故、路障等随机事件,研究车辆出发时间对路径规划的影响,提出TDVRP的混合整数规划公式。随后,MALANDRAKI等[21]又提出一个动态规划公式来解决时间相关的旅行商问题。上述2篇文献通过离散的阶梯函数来计算车辆的行驶时间,其中车辆行驶时间与不同的时段相关,虽然这种计算方法能够体现出速度随时间的周期性改变,但并不满足先进先出(FIFO)准则,这意味着在后面出发的车辆可能会超过另一辆更早开始行驶的车辆,该问题在文献[22-25]中被先后讨论,并且这些学者都根据FIFO准则对时变车辆路径问题进行了建模,之后FIFO准则被广泛应用于时变路网的车辆行驶时间计算过程。
JABALI等[26]构建VRP模型,在时变路网下计算车辆行驶时间、燃料消耗和CO2排放成本,建立的行驶时间模型遵从FIFO准则,之后被FRANCESCHETTI等[10]应用于时变污染路径问题。
为了描述真实的交通状况,本文利用高德地图的海量交通出行数据、车辆轨迹数据和位置数据,并采用实时拥堵延时指数来描述交通状况。拥堵延时指数是指实际出行时间与自由流(道路完全畅通)状态下的比值,值越高代表道路越拥堵,车辆行驶速度也越慢。这里选取2022年11月28日—2022年11月29日武汉市的交通拥堵延时指数,如图1所示(彩色效果见《计算机工程》官网HTML版,下同),选择06:00—22:00的数据进行分析,06:00—07:00道路畅通,07:00—09:00发生了早高峰的拥堵,09:00—17:00道路畅通,随后17:00—19:00又发生了晚高峰的拥堵,在拥堵结束后19:00—22:00车辆再次以自由流速度行驶。显然,路网的交通拥堵情况会随着时间而改变,车辆的速度也会因实际交通状况而变化,这里通过拥堵延时指数观察得到的交通情况与高德地图《2022Q3中国主要城市交通分析报告》的结论相符,即在全天工作时段内,早高峰是07:00—09:00,晚高峰通常是17:00—19:00(由于时区原因,因此乌鲁木齐市的早晚高峰时段有所不同)。

图1 拥堵延时指数Fig.1 Congestion delay index
基于上述分析结果,参考JABALI等[26]提出方法,将1 d的工作时间划分为5个工作时段,并假设每个时段内的交通拥堵是恒定的,即在这一短时间段内车辆的行驶速度保持不变,给出一种遵循FIFO准则的跨时段的路段行驶时间计算方法。图2(a)是不同时段车辆的行驶速度,图2(b)是路径(i,j)上根据车辆的行驶路程和离开时刻计算得到的行驶时间,其中,图2(a)的横轴表示整个工作时间,图2(b)的横轴是车辆离开客户点i的时刻。
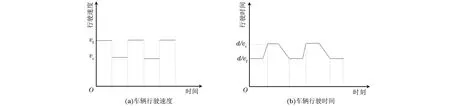
图2 车辆行驶速度和时间Fig.2 Vehicle driving speed and time
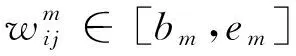
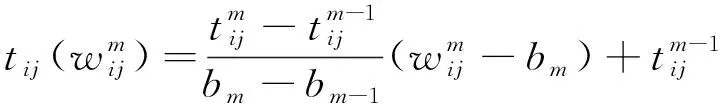
(2)
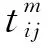
1.5 数学模型
TDGVRPTW的数学模型考虑了2个层次的目标,建立了以最小化碳排放量和总行驶时间的双目标模型,具体如下:

(3)

(4)
约束条件如下:
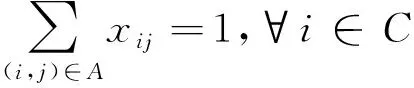
(5)

(6)
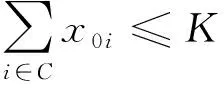
(7)
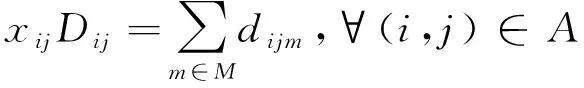
(8)
xijm≤xij,∀(i,j)∈A,m∈M
(9)
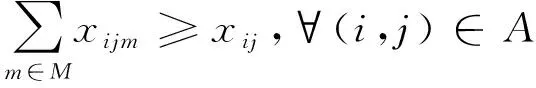
(10)
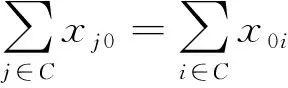
(11)
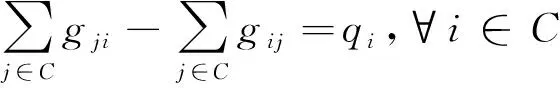
(12)
qixij≤gij≤(W-qj)xij,∀(i,j)∈A
(13)
φi=ai+δi
(14)
li≤φi≤ri
(15)
aj-wi=tij+L(1-xij),
∀(i,j)∈A,L≫0
(16)

(17)
xij∈{0,1},xijm∈{0,1},σk∈{0,1},

(18)
0≤qi≤W,∀i∈C
(19)
式(3)和式(4)分别表示模型的2个目标函数;式(5)和式(6)表示每个客户点只能被车辆访问一次;式(7)确保使用的车辆数不超过配送中心拥有的车辆数;式(8)表示车辆需要完整行驶2个客户点之间的路程;式(9)和式(10)使xij和xijm状态保持一致;式(11)保证车辆从配送中心出发完成运输任务后返回配送中心;式(12)和式(13)是车辆载重约束,确保车辆在行驶过程中的实时载重不超过车辆的最大载重;式(14)和式(15)是时间窗约束,如果车辆提前到达客户点,则需要等待直到客户点允许进行服务的最早时刻再进行服务,故φi=max(ai,li)且φi≤ri,即车辆不能超过最晚服务时间;式(16)是行程时间约束;式(17)是路径(i,j)上行驶时间的计算方式;式(18)和式(19)给出了变量的取值范围。
2 G-IEACO算法设计
VRP是一个NP-Hard组合优化问题,通常使用精确解法、启发式算法和元启发式算法来获得最优解或近似最优解。ACO算法能在动态变化的环境中无需任何外部指导或控制解决几何分布的NP-Hard组合优化问题,由于具有动态规划等传统算法不具备的解决大型组合优化问题的优势而得到了广泛应用。因此,本文对传统ACO算法做出了改进,应用4种邻域搜索算子来加强G-IEACO算法的局部搜索性能,在优化的过程中加入大规模邻域算法进一步提高解的质量,并利用轮盘赌策略改进了算法的状态转移公式。根据TDGVRPTW的特性,加入信息素更新、解的分割和规避拥堵3个重要的改进策略,设计G-IEACO算法。
2.1 编码方式
针对车辆路径问题的特点,采用自然数编码和解码策略,将每一只蚂蚁视为一辆配送车辆,蚂蚁走过的路线即为每一辆车服务的运输路线,配送中心的编号为0,n个客户点的编号序列为{1,2,…,n}。例如,序列{0,2,8,3,0,6,7,5,1,0,9,10,4,0}对应{0,2,8,3,0}、{0,6,7,5,1,0}和{0,9,10,4,0}3条子路径。
2.2 状态转移公式
人工蚂蚁根据状态转移公式决定要访问的下一个节点,传统ACO转移概率由信息素浓度和启发式因子决定,利用轮盘赌可以增强算法的全局搜索能力。计算过程如下:

(20)
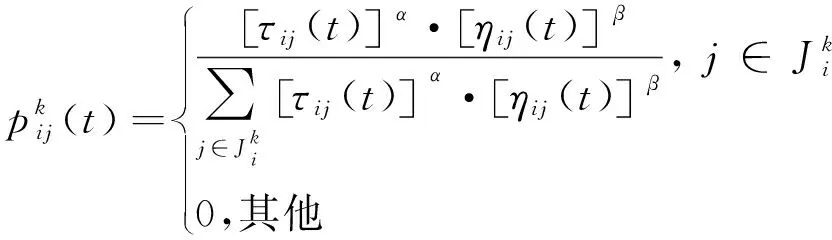
(21)

(22)

2.3 解的分割策略
在G-IEACO算法中的可行解采用自然数编码和解码方式,编码序列分割的目标是从包含所有客户的给定序列中生成使得车辆总行驶时间最小的可行解,并且在所得可行解中每个子路线必须满足约束条件。将文献[27]中的最优分割用于TDGVRPTW,以确定给定编号序列分割的最佳方案,分割算法的基本流程如算法1所示。
算法1分割算法
输入编号序列R={r1,r2,…,rn}
输出可行解
1. F←ArcsCollection(R)∥将输入的客户点编号序列∥转换为一系列的路径(F)
2. S←ShortestPathCollection(F)∥对于每一对客户∥点,找出它们之间的最短路径并放入集合S
3. BestTrvelTime←∞∥初始化最佳行驶时间
4. BestSegmentation←{}∥初始化最佳分割方案为空集
5. for s∈S do
6. if travelTime(s) 7. BestSegmentation←s∥如果是,则更新最佳分∥割方案 8. shortestTravelTime(s)=travelTime(s)∥更∥新记录的最短行驶时间为当前路径的行驶时间 9. end if 10. end for 在分割算法中,将问题定义在一个有向无环图G={N,F}上,其中,N是节点集,节点0表示配送中心,C=N{0}是客户点集合,F是道路网络上连接2个节点的路径的集合。利用最短路径算法可以确定从配送中心到节点n的最短路径集合,最后需要为最优解找到最佳的路径分割方式,选择行驶时间最小的集合的路径。解决方案的有效性只取决于所得路线的数量,并且不能超过配送中心可用车辆的数量。 为了增强算法的局部搜索能力和丰富构造解的多样性,在IEACO算法中加入4种邻域操作算子,具体为路径内插入算子(Op1)、路径间插入算子(Op2)、路径内2-opt邻域算子(Op3)、路径间2点交换算子(Op4)。 1)Op1。随机选择解S中的1条子路径R1,再选出子路径R1中的1个客户点i,将i与R1中所有可行的位置进行交换,记录交换过程中使解S变得最优的插入点point,遍历完整个R1之后再根据point将i插回子路径R1。 2)Op2。从解S中选出客户点最少的子路径R1,再随机从解S中选择另1条子路径R2,确保R2≠R1。选中R1中最后1个客户点i,按照Op1中的插入规则,将R1中的客户点i插入子路径R2。 3)Op3。从解S中随机选出1条满足客户点数量不小于2的子路径R1,选中R1中的2个客户点i和j,i之前和j之后的路径顺序不变,将i到j的路径翻转后与i之前和j之后的路径进行拼接得到新的子路径R′1。 4)Op4。随机选出解S中的2条子路径R1和R2,确保R2≠R1。从R1和R2中各选中1个客户点i和j,交换这2个客户点的位置。 在蚁群算法中,人工蚂蚁由状态转移公式决定要访问的下一个节点,其转移概率由信息素浓度和启发式因子决定,合适的信息素更新策略在整个求解过程中至关重要。因信息素正反馈机制的存在,传统ACO算法在迭代过程中容易造成优质路径上信息素浓度过高,人工蚁群在这些路径上的转移概率过大,从而错过不是当前最优解的较高质量的解,这将会使算法过早收敛而陷入局部最优,为了弥补这种不足,避免过早收敛和陷入局部最优,可以采用更新信息素策略,具体如下: (23) 2)为避免过早收敛陷入局部最优,需要设置较大的信息素挥发因子,而在算法后期,为加快算法的收敛速度,需要设置较小的信息素挥发因子,加大各路径上信息素浓度的差距,使蚂蚁快速向高质量的路径移动。因此,信息素挥发因子应该设置为一个动态的值,式(24)是模拟信息素挥发因子变化的阶段函数: (24) 其中:ρmin表示信息素挥发因子的下限值。 常发性拥堵一般只发生于特定时段,具有一定规律,可以提前进行预测。规避拥堵策略能有效减少车辆行驶时间和环境污染。由于车辆在2个地点之间的行驶时间和碳排放量与行驶的速度有关,而行车速度又取决于车辆所在时段,因此可以通过停车等待来避开严重交通拥堵的时段,最大限度地减少每条路线的行驶时间和碳排放量。假设[Ts,Te]时段是严重拥堵期,车辆位于路径(i,j),Tk是当前时间点,规避拥堵策略具体如下: 1)Tk>Te,表示当车辆行驶到原拥堵路段时,道路上发生的拥堵已经结束,车辆正常行驶,不停车等待。 2)Tk 3)Ts 首先,利用改进的蚂蚁状态转移概率公式构造得到集合P,按照分割策略对P中的自然数序列进行分割解码,解码后通过计算得到集合P中的最优解SbestRoute1。然后,在SbestRoute1的基础上,根据4种邻域算子以及大规模邻域算法得到本次迭代的最优解SbestRoute2,并更新历史最优解SbestEver。接着,在确定SbestRoute2和SbestEver后,按照信息素更新策略更新路径上的信息素,同时重新计算信息素挥发因子ρiter的值。最后,依据规避拥堵策略调度车辆得到最终解决方案Ssolution。G-IEACO具体执行步骤如算法2所示。 算法2G-IEACO算法 输入客户点信息 输出全局最优解Ssolution 1. SbestEver← {} 2. while iter≤itermaxdo 3. ρiter=0.8×ρiter-1 5. 利用分割算法从集合P选择最优解SbestRoute1 6. 应用4种邻域搜索算子和LNS算法对SbestRoute1进行优化获得可行解SbestRoute2 7. if fitness(SbestRoute2)>fitness(SbestEver) 8. 更新历史最优解 9. SbestEver←SbestRoute2 10. end if 11. 根据SbestRoute2和历史最优解SbestEver更新全局信息素和局部信息素 12. δaward=(SbestRoute2-SbestEver)/SbestRoute2 13. 给本次迭代的最优解SbestRoute2额外增加一个信息素奖励值δaward 14. if ρiter>ρmin∩iter>1 15. ρiter=0.8×ρiter-1 16. else if 17. ρiter=ρmin 18. end if 19. end while 20.对SbestEver采用规避拥堵策略,调度车辆获得全局最优解Ssolution 由于没有TDGVRPTW的标准测试库,为了验证算法的适用性与有效性,采用Solomon标准测试集中2种不同规模(客户规模为50和100)的算例进行仿真实验。每个算例都有唯一的配送中心,并按照其地理分布分为R2类和RC2类。在R2类的算例中,客户的地理分布是随机的;在RC2类的算例中,大部分的客户点为随机分布,小部分的客户点为集中分布。此外,R2类和RC2类算例的时间窗较大,每辆车能服务的客户点较多,允许更少的车辆完成配送任务。为符合TDGVRPTW的测试要求,参考文献[28]的方式,并做出如下补充:设定配送中心的工作时间为06:30—22:30,即车辆最早从配送中心出发的时刻为06:30,允许车辆最晚回到配送中心的时刻为22:30,则配送中心在1 d中的服务时长为960 min。 根据城市拥堵延时指数,将1 d的工作时间划分为5段。将06:30—07:00、09:00—17:00和19:00—22:30设置为正常时段,将07:00—09:00和17:00—19:00设为城市交通拥堵时段。在正常时段,车辆的行驶速度为在[50 km/h, 70 km/h]内随机产生;在拥堵时段,车辆的行驶速度在[20 km/h, 40 km/h]内随机产生。ACO算法的参数设置如表2所示。 表2 ACO算法参数设置Table 2 Parameter settings of ACO algorithm 算法代码运行在64位Windows操作系统上,处理器为AMD Ryzen7 5800HS Creator Edition 3.20 GHz,内存为16 GB。 在实验中,以优化车辆碳排放量和车辆总行驶时间为目标。为避免偶然性,减少实验误差,对每1个测试算例均运行10次,从10次运行结果中选出最优解。TT表示车辆总行驶时间,TCO2代表碳排放量,TA表示车辆总使用时间(由车辆总行驶时间、总等待时间和在客户点处服务的时间共同决定)。 为验证车辆规避拥堵策略对车辆行驶时间、碳排放量和总使用时间的影响,选择客户规模为50的R2类和RC2类算例进一步进行测试,如表3所示。由表3可以看出,车辆选择规避交通拥堵期时最多能减少3.96%的碳排放量,平均减少1.67%的碳排放量,而车辆总行驶时间最多能降低16.19%,平均减少7.97%,说明规避交通拥堵策略确实能有效缩短车辆总行驶时间和有效降低车辆碳排放量,实现低碳出行的目的,但由于在避开高峰期时在某些路段选择停车等待的策略,因此可能致使车辆总使用时间会有所增加。 表3 规避拥堵与不规避拥堵的实验结果比较Table 3 Comparison of experimental results between avoiding congestion and not avoiding congestion 又由表3可以看出,与不停车等待主动规避拥堵相比,选择规避拥堵会延长车辆总使用时间,平均延长8.46%的总时间,可见规避拥堵策略对车辆的总使用时间产生的影响比较明显,特别是对于硬时间窗的车辆路径优化问题,在实际运输过程中需要在车辆总使用时间成本与节能环保之间做出取舍权衡。综上,表3的结果符合理论分析结果。 为了进一步评估算法的有效性以及处理较大规模算例的效果,选用客户规模为100的R2类和RC2类算例执行了基准测试,并且将G-IEACO算法与遗传算法(GA)进行实验对比,采用了不同客户点分布情况的算例。为了实验的公平性以及避免偶然误差,GA与G-IEACO算法在每一个测试集中算法均独立运行10次,从10次运行结果中选出最优解进行比较,每个实例的结果如表4所示。 表4 GA与G-IEACO算法实验结果比较Table 4 Comparison of experimental results between the GA and G-IEACO algorithms 根据表4中的数据可分析得出:对于车辆总行驶时间,G-IEACO算法在所有算例上的表现均明显优于GA,最高能缩短25.18%,最低能缩短2.60%,平均节约行驶时间为13.32%;对于车辆的碳排放量(TCO2),G-IEACO算法在所有算例上的计算结果也均优于GA,最高减少24.92%,最低减少1.38%,平均优化率为13.64%。这是由于车辆在2个地点之间的行驶时间和碳排放量与行驶速度有关,根据规避交通拥堵策略,行车速度取决于车辆所在时段,故通过停车等待来避开严重交通拥堵的时段,最大限度地减少了每条路线的行驶时间和碳排放量,因此基于规避交通拥堵策略的G-IEACO算法能有效缩短车辆的行驶时间以及明显降低车辆的温室气体排放。关于车辆的总使用时间,G-IEACO算法在大部分算例上均高于GA,这也从间接验证了规避拥堵策略的有效性,符合表3的实验结果,即规避拥堵策略能明显降低车辆的污染物排放量,但正因为规避过程中的停车等待动作可能在某些情况下会使车辆总使用时间有所增加,即以增加车辆总使用时间为代价,降低了车辆的污染物排放量。 图3给出了GA和G-IEACO算法在客户规模为100的RC208算例上分别运行10次的优化结果,GA在2个目标上的优化结果均劣于G-IEACO算法,并且G-IEACO算法所求解的波动较小、稳定性较强。 图3 2种算法运行10次所得解Fig.3 Solutions obtained by two algorithms running ten times 从节能减排的角度出发,G-IEACO算法在解的质量和稳定性上要优于GA,以增加车辆总使用时间为代价,可以有效规避拥堵路况、降低车辆总行驶时间、减少车辆的油耗和温室气体排放。本节实验结果可以给物流企业在低碳条件下的车辆配送方案提供一定的参考。 针对传统ACO算法在解决VRP时容易陷入局部最优及过早收敛的问题,本文提出一种绿色智能进化蚁群优化算法。该算法设计并应用了多种邻域搜索算子,增强了算法的全局搜索和局部搜索能力,通过大规模邻域搜索算法扩大了搜索空间,提高了解的质量,利用轮盘赌策略改进了算法的状态转移规则,进一步优化结果。同时,针对城市交通拥堵现状以及车辆碳排放情况,引入规避拥堵策略,力求最小化行驶时间和碳排放量,平衡时间成本和环境成本。通过在Solomon测试集的不同类型的算例上进行对比实验,结果表明对于大规模算例,基于时变交通拥堵的G-IEACO算法相比于传统算法能有效降低车辆行驶时间和碳排放量。以上结果验证了该算法在优化城市物流配送方面的潜力,有助于实现绿色物流的目标,并且对于寻求实施低碳、高效物流策略的城市规划者和物流企业具有重要的借鉴意义,同时可以提示企业和政策制定者在制定交通管理和物流策略时,综合考虑交通拥堵模式、环境影响和经济效益,以实现更可持续的城市发展。2.4 邻域算子
2.5 信息素更新策略
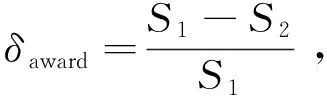
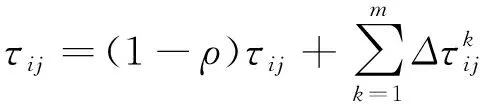
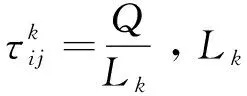

2.6 拥堵规避策略
2.7 G-IEACO算法流程
3 实验与结果分析
3.1 实验设置

3.2 结果分析

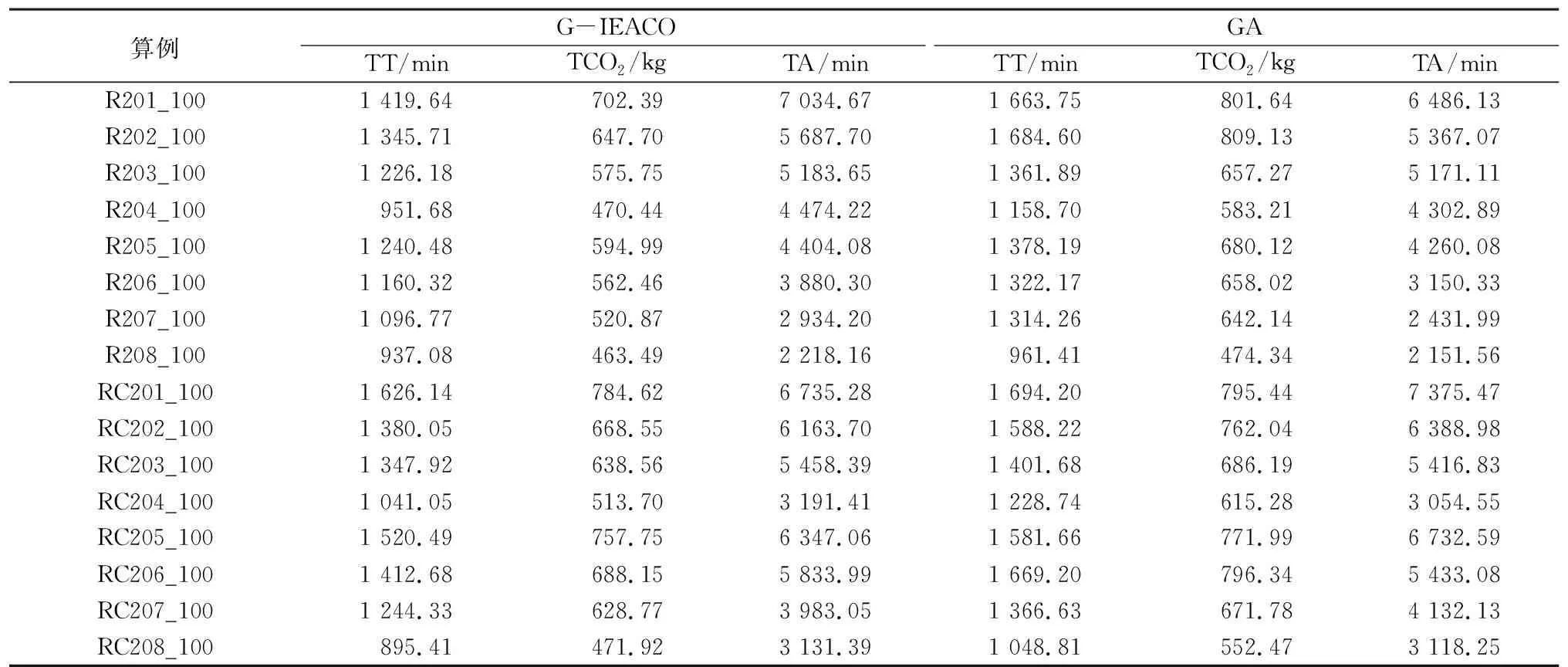

4 结束语

