从重“算法”技巧向“算理”推进

作者简介：金红波（1976～），女，汉族，浙江杭州人，浙江省杭州市萧山区银河实验小学，研究方向：数学教学。

摘  要：文章探索了基于“单位细分”的除数是一位数商中有“0”的除法学习路径，即通过数的组成，从高位起“一位位分，一位位商”，先用横式表达算理，再確定竖式算法。学习路径由以下四个任务构成：366÷2→412÷4→653÷5→148÷6。研究表明，相比对照班学生，实验班学生能更好地掌握商中有0的除法算理，该路径具有可行性。并提出以下建议：引入建议直接复习横式算理表达式；强化单位细分的算理模型，竖式不急于化简；课时划分上可以再斟酌科学合理性。

关键词：算法；算理；单位细分；商中有0；学习路径

中图分类号：G623.5    文献标识码：A    文章编号：1673-8918（2024）08-0066-05

除数是一位数的笔算除法是学习除数是多位数除法的基础，是整数除法算理算法学习重要的一个单元。在人教版教材中给出口算除法3课时，笔算除法7课时，估算和解决问题2课时的教学建议，其中商中有“0”笔算除法在教材中作为一个教学难点，共安排了4课时进行分点突破。北师大版数学教材对商中有“0”的除法的类型划分更细，设置了更多的学习任务以突破难点。这样的编排，使得有关商中有“0”的除法复杂且琐碎。看似详细，实则散乱。教师按课时讲解，更多地侧重每个课时内容笔算算法的指导。学生所学的内容没有一条“藤”串连，知识碎片化，在一定程度上增加了后续知识的学习难度。如何“站在单元的高度，把散点状的知识串联成线，再连成片、构成块”？设计什么样的学习路径才能顺应学生认知逻辑，满足学生自主迁移？

为此，学校在专家引领下，组建了一个核心团队，进行学习路径设计研究。阅读大量国内专家关于单元整体教学及数与运算一致性资料，对国内外不同版本的教材进行对比分析。史宁中教授提出“计数单位”是实现“数与运算一致性”的抓手。巩子坤教授进一步提出整数除法的核心在于“计数单位的细分”，用横式更加容易表达算理，竖式更加容易表达算法。因此，确定把除数是一位数笔算算理定位在单位细分，即“一位位分，一位位商”。这样每一位上计数单位的个数都只要做除法想乘法，做乘法想口诀。在“单位细分”算理统整下，商首位有0、商末尾有0、中间有0等所谓的教学难点不再是难啃的骨头，而只是这个通性通法之中的一个小应用，一个课时就能把商中有0的教学难点一一化解。

基于此，我们将本单元重新组合，去掉口算，设计成单位不用转换、需要单位转换、商中有0这样三节关键课加一节复习课。文章主要研究“商中有0”的学习路径。具体探查以下问题：①以“单位细分”算理贯通商中有0的笔算除法的学习路径是什么？②基于“单位细分”的商中有0的笔算除法学习路径实施效果如何？

一、 研究设计

（一）研究对象

选取YHSY小学三年级甲、乙班作为实验班，按照本研究设计的学习路径教学。同时，选取同一学校平行班丙、丁班为对照班，教师按人教版教材中的课时学习路径进行授课。实验前，对四个班学生进行整十数、整百数除以一位数口算前测评估。结果表明，四个班不存在显著差异。

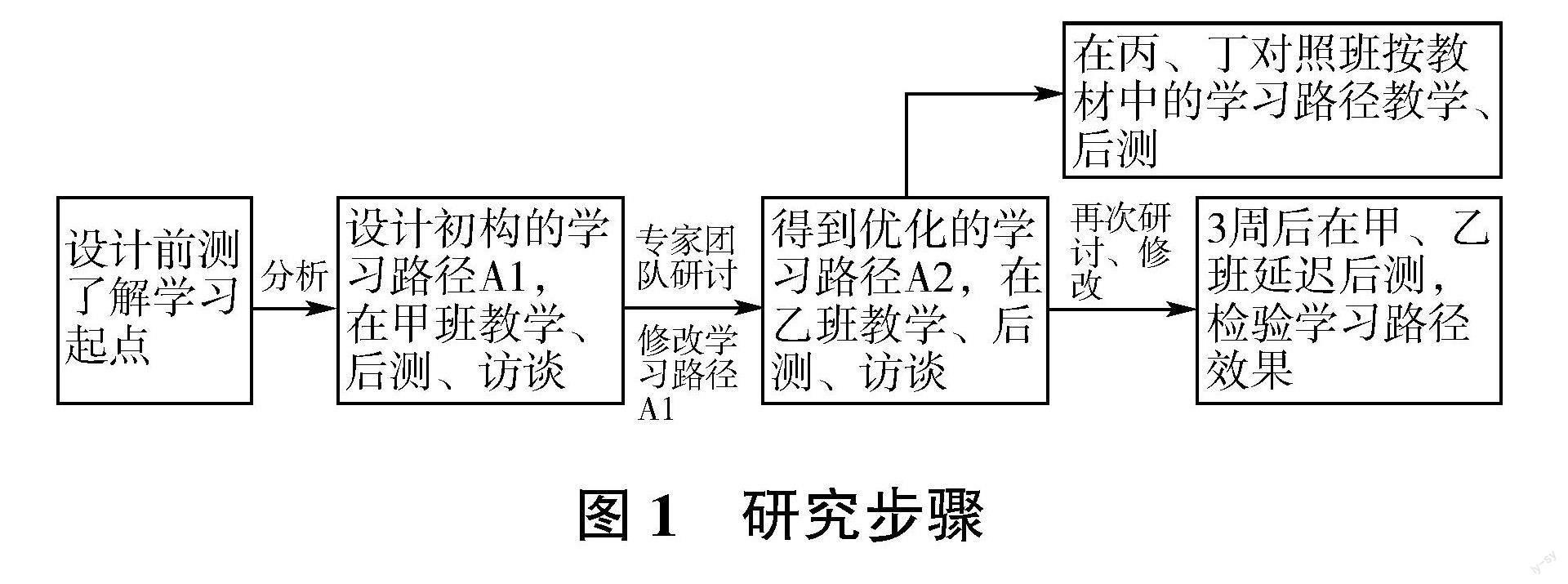
（二）研究流程

图1  研究步骤

（三）理论支撑

1. 基于“单位细分”的除法算理

算理分成：

①单位不需要转化。以484÷4为例，算理过程如下：

484是由4（百）8（十）4（一）组成的

4（百）÷4=1（百），8（十）÷4=2（十），4（一）÷4=1（一），

1（百）+2（十）+1（一）=121

②单位需要转换。以48÷3为例，算理过程如下：

48是由4（十）8（一）组成的

4（十）÷3=1（十）……1（十）

1（十）=10（一）（转化单位）10（一）+8（一）=18（一）

18（一）÷3=6（一）

1（十）+6（一）=16

这就是用横式表达“算理”过程：“单位细分”即“一位位分，一位位商”贯穿始终。然后将算理与竖式算法进行沟通，达到算理与算法互相融合。同时将商中间有0或商末尾有0这些所谓的计算难点也利用“一位位分、一位位商”这样的通性通法一一破解。

2. 表征方式

在除数是一位数的除法教学中，有以下表征方式来说明算理，如表1所示。

程序表征通过运算法则列竖式进行整数除法运算，如48÷4。

直观表征利用具体物体说明运算的合理性，如分小棒、小方块等。

语言表征用语言描述运算的合理性，如148÷6可以这样描述一个百除以8不够除，就用14个十除以6，商2写在十位上余2个十，余下的2个十和8个一合起来是28个一除以6，商4写在各位商，余4。

抽象表征通过推理来描述运算的合理性，如基于“单位细分”来推演除数是一位数除法的算理。

（四）问卷及数据处理

授课后，对实验班和对照班进行后测练习，习题如下：

403÷3  608÷4  413÷8  680÷4

①实验班作业要求：先用横式表达算理，再用竖式表达算法。

②对照班作业要求：直接用竖式计算，并能用文字解释每一层余下数表示多少。

测试后对问卷进行赋分，实验班正确写出横式得1分，正确写出竖式得1分，一题2分；对照班能正确写出竖式得1分，文字解释正确得1分，一题2分。满分8分。

二、 研究路径与分析

（一）已授课和前测

商有0的在本单元整合后是第三课时，前2个课时已把“算理”教授完毕。根据前两堂课的后测，也就是本次授课的前测。评估分析后发现两个班得分率如表2所示。

（二）初构的学习路径A1

1. 路径呈现

图2  初构的学习路径A2

任務一：第一个环节是4道关于0的口算题，引出0；第二个环节出示人民币：1张百元纸币要平均分给5名学生怎么分？1张10元呢？目的是通过人民币之间的换算，让学生理解单位细分方法。

任务二：情景题引入新课，最高位有0的除法，重点突破百位不够分，需要转化成低一级单位，才能继续分，百位没有分成功，就在百位上商0。

任务三：自主探究商末尾有0除法。这个任务是在突破任务二的前提下讨论的。

任务四：在突破最高位商0，末尾商0的前提下，举一反三，练习商中间有0的一个例题。进一步巩固，当某一位不够分，就商0，并且将其转化成低一级单位继续分。

2. 存在问题

分析学习单完成情况，结果显示只有部分学生会把横式算理和竖式算法融合起来，即：横式是分几步，竖式就有几层。在后测错误情况分析中，常见错误如下：其一，最高位不够分单位需要转化的横式表达学生书写时会漏掉百位分的过程。其二，百位（最高位）不够商1时，学生笔算会把百位和十位合并分的结果写在百位上，如图3所示；其三个位（末尾）不够商1，学生会出现无商的现象，如图4所示。

针对以上错误情况，分析初构的学习路径A1存在以下问题：

①任务一复习回顾未凸显“单位细分”用横式表达算理的重要性。导致新授课学生横式算理的书写推进缓慢。

②例题选择和顺序不利于算理推进，无形中给教学带来了羁绊。

初构路径A1：商首位有0→商末尾有0→商中间有0

例题选取：148÷6→245÷8→208÷2→216÷2

③过于强调笔算化简方法，算理和算法一致性没有得到很好的体现，导致学生不能把横式算理和竖式算法一一对应，融为一体。

3. 改进建议

（1）去掉情景引入，凸显“单位细分”算理过程

其一：任务一去掉口算引入和人民币引入，而是直接通过一道不需要单位转化的计算题，来复习单位细分的横式过程并规范格式。

其二：任务二去掉情景引入，重点讨论商中有0的算理过程。

（2）精选例题，调整顺序

针对路径1出现的问题，我们将学习路径调整为：复习算理→商中间有0→商末尾有0→商首位有0，对应的例题为：

366÷2→412÷4→653÷5→148÷6

（3）淡化化简技巧，凸显算理和算法一致性

强化单位细分的过程，旨在学生头脑中建立算理和算法一一对应的模型（图5），不急于化简。化简则是熟练之后水到渠成的事情。

图5  凸显算理和算法一致性

（三）优化的学习路径A2

1. 路径呈现

图6  优化的学习路径A2

本节课的教学目标是：理解“被除数的某位不够商1时，应在这一位商0”的算理。与路径A1相比，路径A2的教学更加注重横式算理推进巩固，教学环节更加简洁。一道题复习巩固算理，唤起回忆。新课三道题，从商中间有0开始演绎，然后是商末尾有0，最后是首位商0。如何运用“单位细分”算理来突破商中有0的教学难点。下面将借助部分教学片段来说明。

（1）出示题目：412÷4=

师：同桌讨论后完成学习单第1题用横式记录计算的过程。

生：安静记录，后交流算理。

生1：分成2步。4（百）÷4=1（百）。12（一）÷4=3（一）

师：你是怎么想的？（图7）

图7  分2步作业单

生1：因为1（十）÷4除不了，那就把个位加上一起除。

生2：先把412分成4个百、1个十和2个一；然后4（百）÷4=1（百），1（十）÷4除不了商就是0（十）还余下1（十），然后1（十）=10（一）再加上个位上的2个一，就是12个（一），然后12（一）÷4=3（一）答案就是103（图8）。

图8  分3步作业单

师：我们比一比分2步的学生，和分三步的学生，分三步的学生多的是哪个步骤？

生：多的是1（十）÷4不够除，就商0还余1（十）

小结：两步的学生其实脑子里也想到了1（十）不够分，只是没有把这一步写出来。而三步的学生正好把这一步补上了，不够商1，可以商0。没有分成功的1（十）就余下来。所以这道题完整的也是3步。

（2）把横式的过程用竖式记录

师：小朋友会把刚才讨论的三个步骤用竖式记录下来吗？写在学习单对应的方框内。

生：安静完成作业单。

师：展示学生作业单，说说每一层对应的是横式的哪一步。

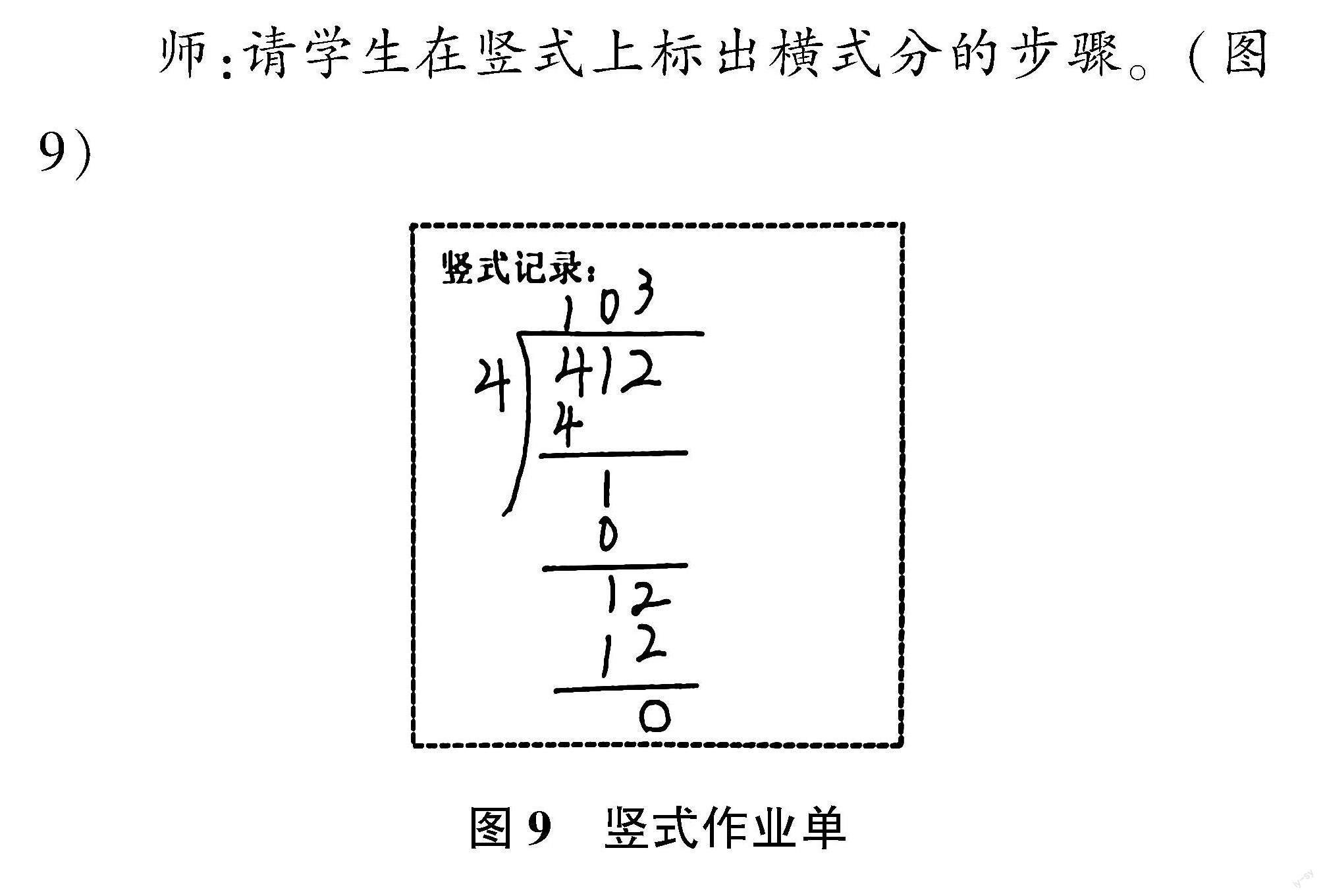
师：请学生在竖式上标出横式分的步骤。（图9）

图9  竖式作业单

这节课的重点就是突破商的某一位不够分时，就商“0”并把余下的数转化成小一级的计数单位。在探究新课时，选择从商的中间有0开始，更能让学生理解“十位不够分的时候，必须把十位的计数单位转化成更小的计数单位，即“1（十）÷2=0（十）……10（一），10（一）+2（一）=12（一）”不够分的十位就写“0”的道理。在理解横式的基础上，用竖式来表达算理，能在竖式中找到横式的3步。

2. 路径效果检验

（1）甲、乙实验班即时教学效果检验

在路径A1和路径A2实施后，依次对甲、乙班学生进行后测，统计学生班级平均分，其中乙班学生的班级平均分（6.87分）明显高于甲班（4.80分）。通过独立样本t检验，结果显示，甲、乙班的得分（t=2.285，p<0.05）存在显著性差异。由此可见，路径A2的效果优于A1。

（2）实验班、对照班即时后测分析

对“实验班”“对照班”学生即时后测进行独立样本t检验，结果显示，（t=2.846，P＜0.05）存在显著差异。由此可见，实验班学习路径与对照班学习路径相比，实验班的学习路径更加有利于学生理解算理，使得横式和竖式能够很好地融合在一起。用横式疏通算理，用竖式把算理和算法融会贯通。

（3）甲、乙试验班延迟后测分析

授课结束3周后，对两个实验班进行延迟后测。结果显示，甲班得分率降低了12.82%，乙班降低了5.35%，这说明乙班学生对商中有0这一课，算理掌握更加到位，教学效果持久性更强。

3. 存在不足及建议

虽然优化后的A2的学习路径相比A1已经有了很大的改进，但在教学中，仍然发现了诸多问题。如部分学生在转化成下一级单位时，会跳级。即：百位余下的数会转化成几个一，使得继续分的过程变得非常复杂。建议在课时划分时是否可以考虑增加一节课教学48÷5用小棒实践操作，让学生经历4（十）÷5不够分，必须把4捆小棒全拆了和8根小棒合起来，才能分成功的体验。然后再教学148÷6，直观表征和抽象表征结合。第四课时重点教学商中间有0和末尾有0的除法只用抽象表征。

进一步优化后的学习路径A3和路径A2变化不大，只是完善了例题出示的形式变化，故不再详述。

三、 研究结论与启示

（一）研究结论

（1）在除数是一位数商中有0的除法学习路径中，以单位细分的通性通法贯穿始终，即“一位位分，一位位商”。在教学过程中先教学商中间有0，再末尾有0，最后首位有0，把商中有0的教学难点也统整到了单位需要转化和单位不需要转化两类算理当中，0只是通性通法下的一个小技巧。从而实现数与运算一致性的核心理念下单元整体教学的目标。

（2）研究数据表明，借助该学习路径，本研究中的学生能够借助“一位位分，一位位商”理解运算的算理，理解商0的意义，获得较高的计算正确率。与教材中的学习路径相比，本研究设计的学习路径有利于学生理解除数是一位数除法笔算的算理。

（二）研究启示

（1）学生层面：本次学习路径的探究，对标《义务教育数学课程标准（2022年版）》理论：核心素养具有整体性、一致性和阶段性。要让学生体会数和运算本质上的一致性，形成运算能力和推理意识。在之后的复习课中，借助“单位细分”这个算理模型迁移学习三位数除以两位数，四位数除以两位数，学生也能融会贯通，正确计算。学生对整数除法有了整体的、系统的认识，理清了知识的来龙去脉，有助于持久记忆、深度理解和广泛迁移。正如弗赖登塔尔所说：不要教孤立的片段，应该教连贯的材料，因为有联系的事物学得快，记得牢。

（2）教师层面：本次研讨之后，我们将在此基础上继续完善和改进，为下一次实践探究提供宝贵的数据和建议。虽然这个过程艰辛甚至要反复推倒重来，但对一线教师，无疑是一次对单元进行大刀阔斧整合的嘗试，打破单一课时的思维，并且对数与运算一致性的理解有了突破性的认识。本次教研方案被评为区级二等奖，研究成果总结报告获一等奖，数学教研组被评为区级优秀教研组，二位教师的教学设计获区一等奖，一位获二等奖。一位教师在区级单元整体教研活动中做了关于单元框架的讲座，二位教师在“国培”班中上了展示课。学校教师在专家团队引领的教研氛围中，持续提升教师的教研水平，最终受益于学生。

参考文献：

［1］朱俊华.小学数学单元整体教学的实践探索［J］.江苏教育（小学教学版），2022（3）：47-51.

［2］赵莉，吴正宪，史宁中.小学数学教学数的认识与运算一致性的研究与实践以“数与运算”总复习为例［J］.课程·教材·教法，2022，42（8）：122-129.

［3］巩子坤，刘萍.论数的概念与运算的一致性之三：整数运算算理、算法的一致性［J］.小学数学教师，2022（10）：77-81.

［4］中华人民共和国教育部.义务教育数学课程标准（2022年版）［S］.北京：北京师范大学出版社（集团）有限公司，2022.

［5］弗赖登塔尔.作为教育任务的数学［M］.陈昌平，唐瑞芬，译.上海：上海教育出版社，1995.