抽象函数周期性学习的“四境界”

⦿ 安徽省合肥市第十一中学 詹步创

抽象函数问题是近年来高考命题的热点,因为它既能反映数学的本质特征,又能体现新课标对数学抽象和逻辑推理等核心素养考查的要求.在对抽象函数性质的考查中,特别是周期性问题比较隐蔽,很难把握,在学习中不少学生只见树木,不见森林,很有畏难情绪,甚至部分教师在教学中也是蜻蜓点水,浅尝辄止.本文中将周期性的深度学习分为“四个境界”,层层递进,结合近年来高考试题对此进行剖析,供读者参考.

1 境界一:由周期性的定义及变式推出周期性

定义:对于f(x)定义域内的每一个x,都存在非零常数T,使得f(x+T)=f(x)恒成立,则称函数f(x)具有周期性,T叫做f(x)的一个周期,则kT(k∈Z,k≠0)也是f(x)的周期,所有周期中的最小正数叫f(x)的最小正周期.

变式设a是非零常数,若对于函数y=f(x)定义域内的任一自变量x有下列条件之一成立,则函数y=f(x)是周期函数,且2|a|是它的一个周期.

A.-3 B.-2 C.0 D.1

分析：本题考查数学抽象、数学运算和逻辑推理等核心素养.该题的关键是通过题目所给条件得出相应的等式,进而对等式迭代得出函数的周期性,灵活赋值及掌握变式是解决此类问题的关键.x,y是两个未知量,对x,y其中一个进行赋值,令y=1,得f(x+1)+f(x-1)=f(x),用“x+1”代换“x”得f(x+2)+f(x)=f(x+1),两式联立,求出周期性.

2 境界二:由函数的奇偶性、对称性推出周期性

解决已知奇偶性和对称性推出周期性的问题时,首先需要掌握对称性的相关知识,可类比正弦函数、余弦函数.而对称性包括直线对称和点对称,尤其是函数图象关于点对称的问题处理至关重要.

注：f(a+x)=f(a-x)⟺f(x)=f(2a-x)⟺f(-x)=f(2a+x).

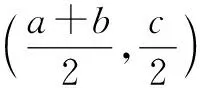
注：f(a+x)=-f(a-x)⟺f(x)=-f(2a-x)⟺f(-x)=-f(2a+x).

例2已知函数f(x)的定义域为R,f(x+2)为偶函数,f(2x+1)为奇函数,则( ).(B)

C.f(2)=0 D.f(4)=0

分析：若f(x+a)为奇函数,则f(x)的图象关于点(a,0)对称;若f(x+a)为偶函数,则f(x)的图象关于直线x=a对称.函数f(x+a)的奇偶性问题等价于f(x)的对称性问题,该题的本质是f(x)的“一点、一直线”对称性问题.

结论1：若f(x)的图象同时关于直线x=a与x=b对称,则f(x)为周期函数,且T=2|a-b|(a≠b).

结论2：若f(x)的图象关于点(a,0)与点(b,0)中心对称,则f(x)为周期函数,且T=2|a-b|(a≠b).

结论3：若f(x)的图象关于点(a,0)中心对称,且关于直线x=b轴对称,则f(x)为周期函数,且T=4|a-b|(a≠b).

结论4：若f(x)的图象关于点(a,c)中心对称,关于直线x=b轴对称,则f(x)为周期函数,且T=4|a-b|(a≠b).

结论5：若f(x)是奇函数,且图象关于x=a轴对称,则f(x)是周期函数,周期为4|a|.

结论6：若f(x)是偶函数,且图象关于x=a轴对称,则f(x)是周期函数,周期为2|a|.

结论7：若f(x)是奇函数,且图象关于点(a,0)对称,则f(x)是周期函数,周期为2|a|.

结论8：若f(x)是偶函数,且图象关于点(a,0)对称,则f(x)是周期函数,周期为4|a|.

注：结论3可以理解为是结论4的推论,结论5～8可以理解为是结论1～3的推论.

3 境界三:由原函数与导函数的对称性关系推出周期性

原函数与导函数的图象有着密切的联系,导函数图象不仅可以反映原函数的变化率和单调性,还可以描述它们的对称性关系.

C.f(-1)=f(4) D.g(-1)=g(2)

拓展:设函数f(x)及其导函数f′(x)的定义域均为R,则有以下结论成立.

结论9：若f(x)的图象关于直线x=a轴对称,则f′(x)的图象关于点(a,0)中心对称.

结论10：若f(x)的图象关于点(a,0)中心对称,则f′(x)的图象关于直线x=a轴对称.

结论11：若f′(x)的图象关于直线x=a轴对称,则f(x)的图象关于点(a,f(a))中心对称.

结论12：若f′(x)的图象关于点(a,0)中心对称,则f(x)的图象关于直线x=a轴对称.

注：熟练掌握原函数与导函数对称性之间的关系是有利于解题的.

4 境界四:构造三角函数模型推出周期性

A.-21 B.-22 C.-23 D.-24

分析：本题从函数f(x)的角度考虑较为繁琐,由于题目所给的条件中,函数g(x)的相关要素较多,可以考虑将两个等式中的f(x)消去,得到g(x)的表达式,借助于g(x)的对称性求得函数g(x)的周期,再构造三角函数解决问题.

5 总结

周期性的学习可以划分为四个境界,每个境界都有其独特的特点和层次.这些境界层层递进,帮助学生逐步理解和掌握周期性的概念和性质.

在境界一中,学生需要理解周期性的基本定义,并学会通过变式推导出周期性.周期性指的是函数在一定规律下重复出现的性质.学生应该能够判断一个函数是否具有周期性,并且能够找到该函数的周期.通过学习境界一,学生可以建立对周期性的初步认识.

境界二的重点是由函数的奇偶性和对称性如何推出周期性.奇偶性和对称性是函数的重要特征,通过分析函数的奇偶性和对称性,可以判断函数是否具有周期性.例如,如果一个函数是偶函数,则它具有关于y轴的对称性,从而可以推断它是周期性函数.学生需要学会运用奇偶性和对称性的概念,以及相关的性质和定理,来判断函数的周期性.

境界三涉及由原函数与导函数之间的对称性关系如何推出周期性.原函数与导函数之间存在一定的对称性关系,通过研究这种对称性关系,可以进一步推导函数的周期性.例如,如果一个函数的导函数具有某种对称性,那么可以推断该函数具有相应的周期性.学生需要深入了解原函数和导函数之间的关系,以及如何利用这种关系来判断周期性.

在境界四中,学生将学习如何通过构造三角函数模型来推出周期性.三角函数是一类常见的周期函数,通过构造三角函数模型,可以更直观地描述和理解抽象函数的周期性特征.学生需要学会选择适当的三角函数,调整其参数和变量,以构造出符合要求的周期函数模型.这样的学习可以帮助学生深入理解周期性的本质,并提高解决周期性问题的能力.

综上所述,上述四个境界层层递进,每个境界都有其独特的特点和层次.通过逐步深入学习,学生可以全面理解抽象函数的周期性,并培养数学建模和解决实际问题的能力.这种学习方法不仅有助于应试考试,还能够为学生的数学学习打下坚实的基础.因此,学生应该注重在每个境界上的学习,并逐步提升对周期性问题的理解和应用能力.