采用模糊补偿滑模控制器的空间柔性机械臂振动抑制方法

尚东阳, 李小彭, 尹 猛, 李凡杰, 周赛男

(1. 东北大学 机械工程与自动化学院, 沈阳 110819; 2. 中国科学院深圳先进技术研究院, 广东 深圳 518055)

随着机器人技术的不断发展,机械臂已经在航空航天领域获得了广泛的应用。空间机械臂的提出和应用可以协助宇航员更加便利地开展舱外检修任务。随着空间机械臂结构尺寸的增大,更多的空间机械臂可以实现飞行器的捕捉与释放。关于空间机械臂的研究已经取得了丰硕的成果。太空机器臂技术出现于20世纪80年代,其中最具代表性的机器臂是SPAR Aerospace开发的SSRMS机械臂[1],该机械臂应用于国际空间站。除了SSRMS机械臂外,典型的空间机械臂还包括Robot Technology Experiment[2]、Engineering Test Satellite-VII[3]等。由于火箭发射成本和运载能力的限制,空间机械臂均具有轻质的特点。相比较于刚性机械臂,柔性机械臂具有轻质、大操作范围的优势。基于柔性机械臂的优势,文献[4-5]将柔性机械臂应用于空间站或者飞船提出了空间柔性机械臂的概念。空间柔性机械臂的长度可达十几米以满足较大的运动范围和操作空间。空间柔性机械臂较大的操作空间且轻质化的结构材料意味着空间机械臂一般为细长结构,且必须采用密度、刚度较小的材料,这就会导致空间机械臂的杆件的弹性变形较为明显。由此,空间柔性机械臂在运动过程中容易出现振动的现象。空间柔性机械臂的振动会影响操作精度甚至是空间站的飞行安全。因此,空间柔性机械臂的振动抑制研究对于空间机器人的发展具有重要的意义。

为了实现空间柔性机械臂的高精度控制,首先要建立精确的动力学模型。空间柔性机械臂动力学建模的难点在于非线性变形的描述。随着研究的深入,柔性结构的多维变形逐渐得到许多学者的关注。文献[6]使用有限元法建立了考虑三维变形的柔性梁动力学方程。文献[7]建立了考虑二维变形的水下柔性机械臂的动力学方程。在柔性结构动力学建模过程中考虑的非线性因素越多,建模精度越高。文献[8]认为柔性结构可以等效为柔性梁模型。一般认为,柔性梁模型可以用欧拉-伯努利梁模型[9]和铁木辛柯梁模型[10]表示。两种梁模型的主要区别在于是否考虑剪切变形。此外,空间柔性机械臂转动中受到的外界干扰同样会加剧振动。文献[11]使用LuGre模型描述外界干扰。虽然考虑多种非线性因素可以提高空间柔性机械臂的建模精度。但是所建立的空间柔性机械臂数学模型与真实的模型之间仍存在着建模误差。这是因为在动力学建模中不可能考虑所有的非线性因素。此外,例如外界干扰模型中的参数会随着环境发生改变。由此,在空间柔性机械臂的建模中无法准确地用数学表达式表征外界干扰。如何在空间柔性机械臂控制律的设计中补偿建模误差成为动力学和控制领域研究的热点话题。

随着空间机械臂技术的不断发展,对于机械臂操作精度的要求不断提高。要想实现空间柔性机械臂的高精度控制,需要将动力学模型的建模误差予以考虑。随着抗干扰控制策略和自适应控制策略的成熟,许多学者使用这两种控制策略提高空间机械臂的操作精度。文献[12]使用扩张状态观测器提高空间机械臂的控制精度。文献[13]提出了一种自适应控制策略来控制自由漂浮空间机械臂的末端执行器,从而减小了跟踪误差。经典控制理论无法消除非线性因素对空间柔性机械臂的影响。此外,滑模控制在机器人控制领域得到了广泛的使用。文献[14]采用实时滑模控制策略对空间机械臂进行控制。随着控制理论的发展,以神经网络和模糊规则为代表的智能控制方法可以在线辨识动力学模型的不确定成分。神经网络和模糊规则的万能逼近特性非常适合于辨识因建模误差引起的不确定成分。文献[15]提出了一种自适应神经网络控制器来控制空间机械臂。文献[16]提出了神经网络在柔性机械臂中的应用,并通过试验证明了神经网络补偿的有效性。因此,可以采用神经网络或模糊规则来识别空间柔性机械臂动力学模型的建模误差,并通过对建模误差的补偿来提高控制精度。

本文使用假设模态法和拉格朗日原理建立了考虑非线性变形和外界干扰的空间柔性机械臂动力学模型。采用模糊规则识别空间柔性机械臂动力学模型的建模误差。将模糊规则辨识的结果补偿到控制律中,以此提高驱动力矩的精度,进而保证空间柔性机械臂的转动精度。本文的创新主要有两个方面。第一个方面是在空间柔性机械臂的动力学建模过程中同时考虑纵向变形和横向变形。相比较于文献[17]所建立的柔性机械臂动力学模型,本文再考虑了柔性结构的纵向变形,这极大地增加了柔性机械臂动力学建模的难度。第二个方面是提出一种模糊规则辨识的控制策略以提高空间柔性机械臂的转动精度,进而减弱机械臂的振动。在控制律的设计上,使用模糊规则辨识补偿建模误差以提高控制精度。通过提高转动精度的方式间接地减弱空间柔性机械臂的振动幅值。

1 空间柔性机械臂动力学建模

空间柔性机械臂可以安装于空间站,如图1(a)所示。空间机械臂中末端执行器的质量和转动惯量远小于柔性旋转结构,由此可以认为执行器和柔性结构成为一个整体。空间柔性机械臂可以等效为由电机驱动的柔性结构,其等效模型如图1(b)所示。在空间柔性机械臂转动时,空间站处于相对稳定的飞行状态。在本文中忽略了空间站机动对于空间柔性机械臂的影响。为了便于建立动力学模型,本文将空间柔性机械臂等效为柔性梁模型。空间柔性机械臂的横向变形表示为w(x,t);纵向变形表示为u(x,t)。空间柔性机械臂的物理参数表示如下:l表示长度;m表示质量;EI表示抗弯刚度。空间柔性机械臂在驱动力矩Ta和干扰Mf作用下的转角θ与固定坐标系XOY和随动坐标系xOy之间的角度相一致。空间柔性机械臂在转动过程中会出现横向变形。根据文献[18]可得到横向变形的表达式,如式(1)所示

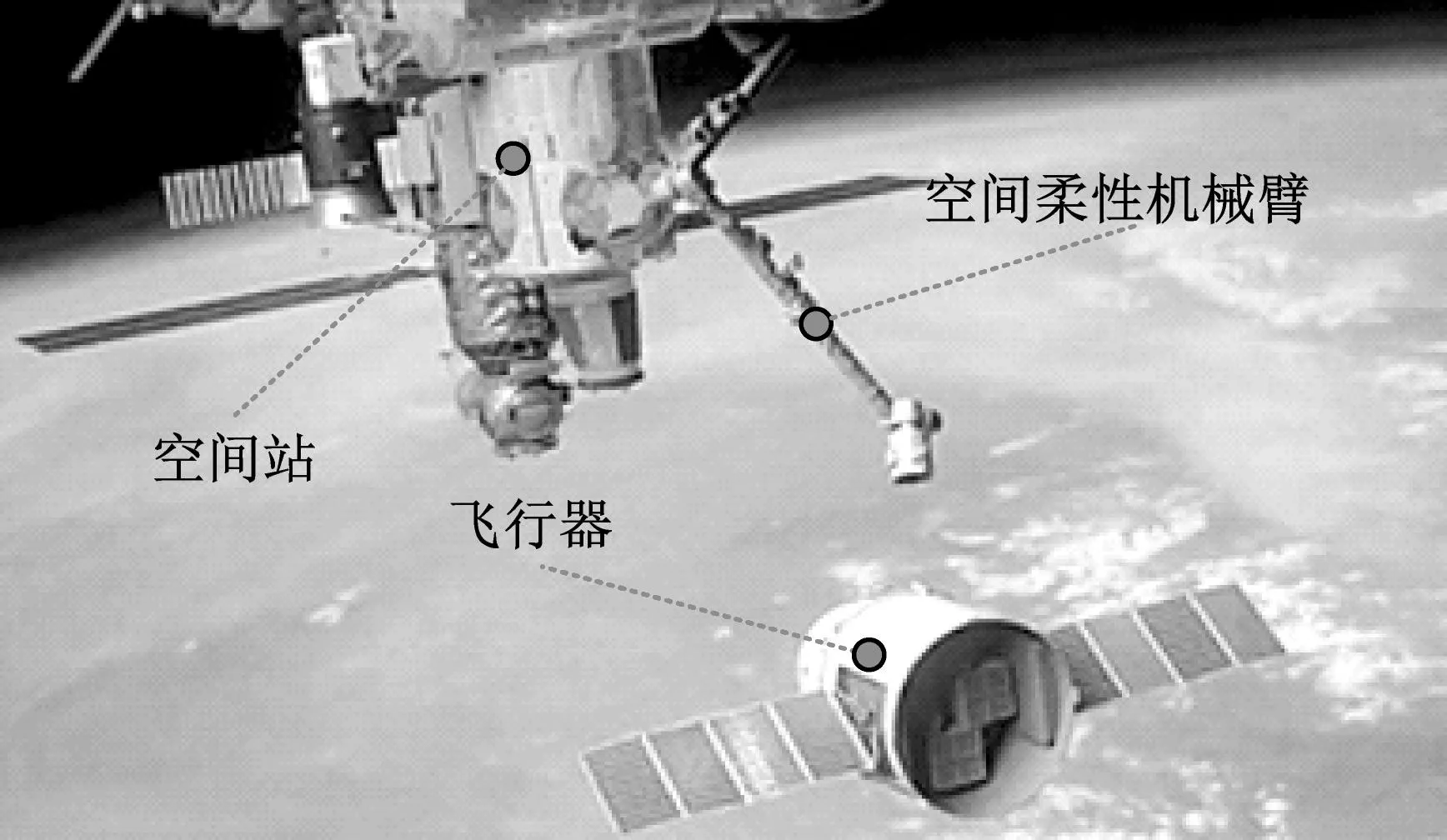
(a) 空间柔性机械臂假想图

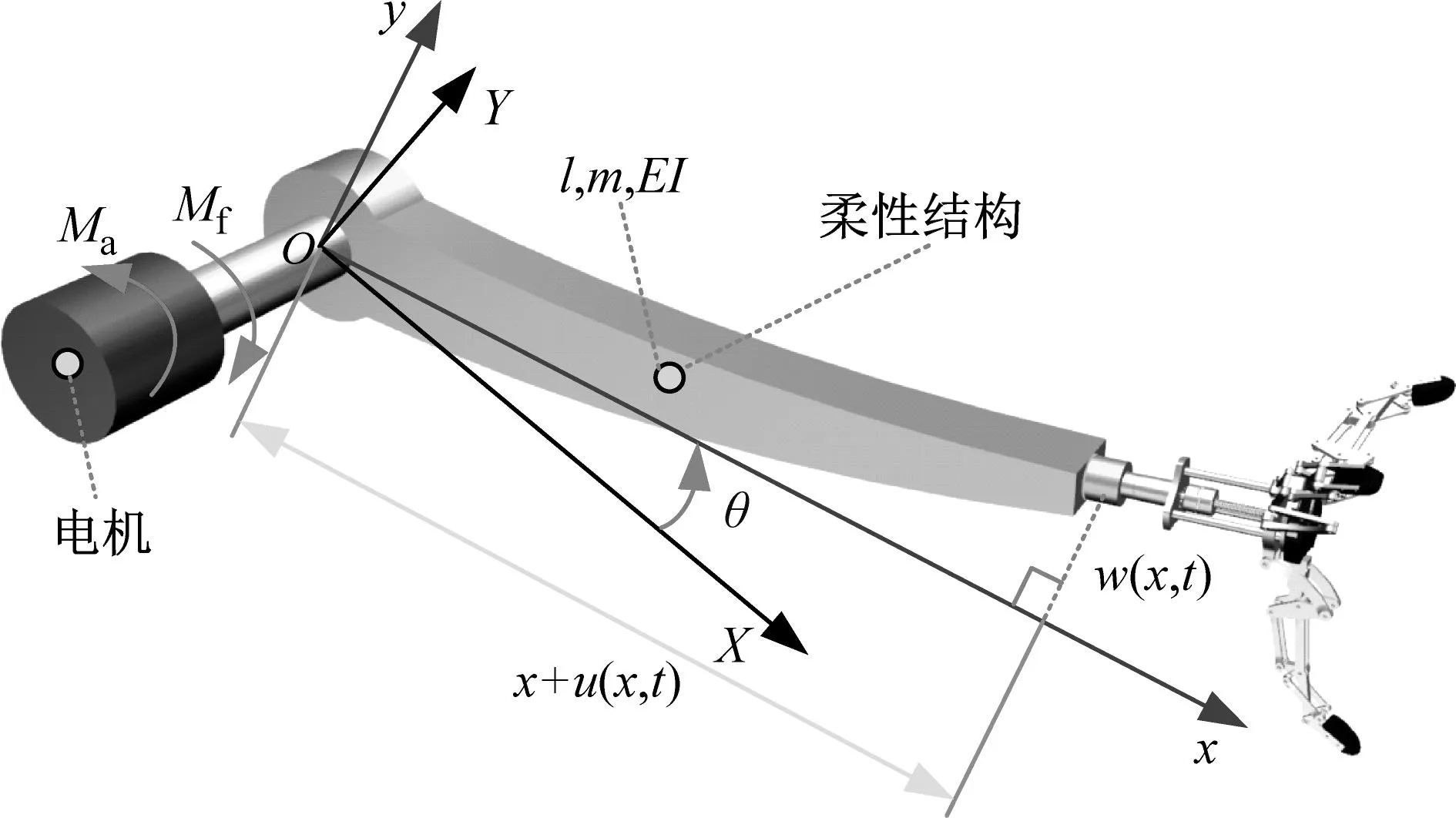
(b) 空间柔性机械臂等效模型图图1 空间柔性机械臂示意图Fig.1 Schematic diagram of space-flexible manipulator

(1)

式中:φi(x)为第i阶模态函数;ηi(t)为第i阶模态坐标;∂i为第i阶模态函数特征根值。

根据文献[19]可得横向变形和纵向变形之间的耦合关系,如式(2)所示。

(2)

根据式(2)可得式(3)

(3)

根据式(3)可得到纵向变形的表达式,如式(4)所示

(4)

在获得柔性结构的纵向变形和横向变形的表达式后可得到柔性结构上任意一点在固定坐标系的位置如式(5)所示

(5)

式中:x为柔性结构上任意一点的横坐标;u(x,t)=u,w(x,t)=w。为了方便书写,用“·”表示对时间t的偏导数。同理,用“′”表示对横坐标x的偏导数。

根据式(5)可得到式(6)

(6)

根据式(6)可得到柔性结构的动能,如式(7)所示

(7)

同理,可得到柔性结构的势能,如式(8)所示

(8)

根据拉格朗日动力学方程,可以得到式(9)

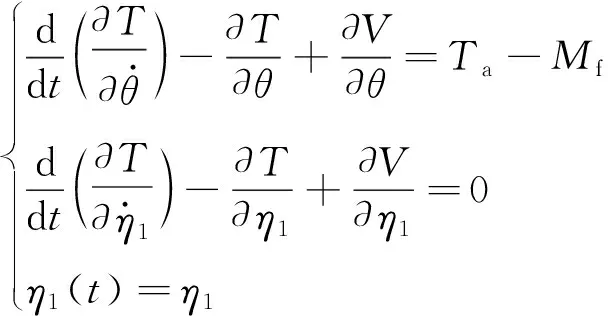
(9)

由于二阶及高阶模态对于柔性机械臂建模精度的影响十分有限。本文为了减少计算量,在建立动力学方程时仅考虑一阶模态。将空间柔性机械臂的动能和势能代入式(9)后可得到式(10)

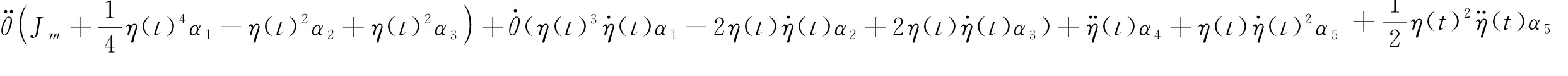
(10a)

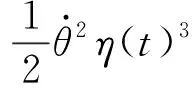
(10b)

式中,αi表示动力学模型的参数,其表达式如附录A所示。

式(10)即表示考虑二维变形的空间柔性机械臂的动力学方程。

如果忽略纵向变形,则柔性结构上任意一点的位置如式(11)所示

(11)

根据式(11)可得到柔性结构的动能,如式(12)所示

(12)

将式(12)所示的动能和式(8)所示的势能代入式(9)中可得到式(13)

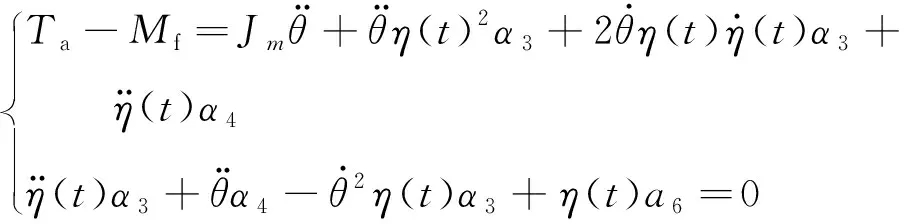
(13)

式(13)即表示仅考虑一维变形的动力学方程。

如果去除动力学方程中的非线性项,则可以得到式(14)

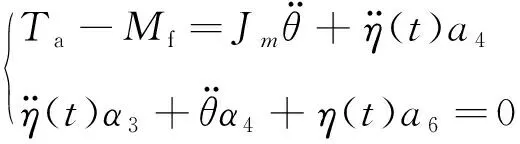
(14)

式(14)即表示去除非线性项所得到的动力学方程。

动力学方程中的外界干扰可以用LuGre模型表示,其表达式如式(15)所示

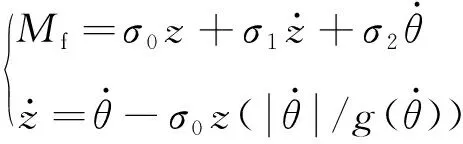
(15)

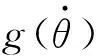
(16)

其中:Mc表示库伦摩擦力矩;Ms表示静摩擦力矩;θs表示Stribeck速度。

2 动力学建模精度分析

为了研究非线性项对于空间柔性机械臂建模精度的影响,选择Damaren提出的单杆演算法作为柔性结构转角和时间的变化函数[20],其表达式如式(17)所示

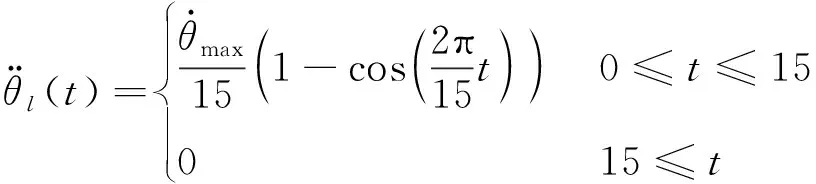
(17)

本文通过变形精度衡量动力学建模精度。采用角度相关法计算柔性结构的变形。所谓的角度相关法指的是:首先忽略结构的柔性因素,将柔性结构认为是刚性结构。然后根据刚性负载和转角加速度计算所需的驱动力。最后将所计算的驱动力矩输入空间柔性机械臂动力学模型,得到柔性结构的变形,其计算流程图如图2所示。

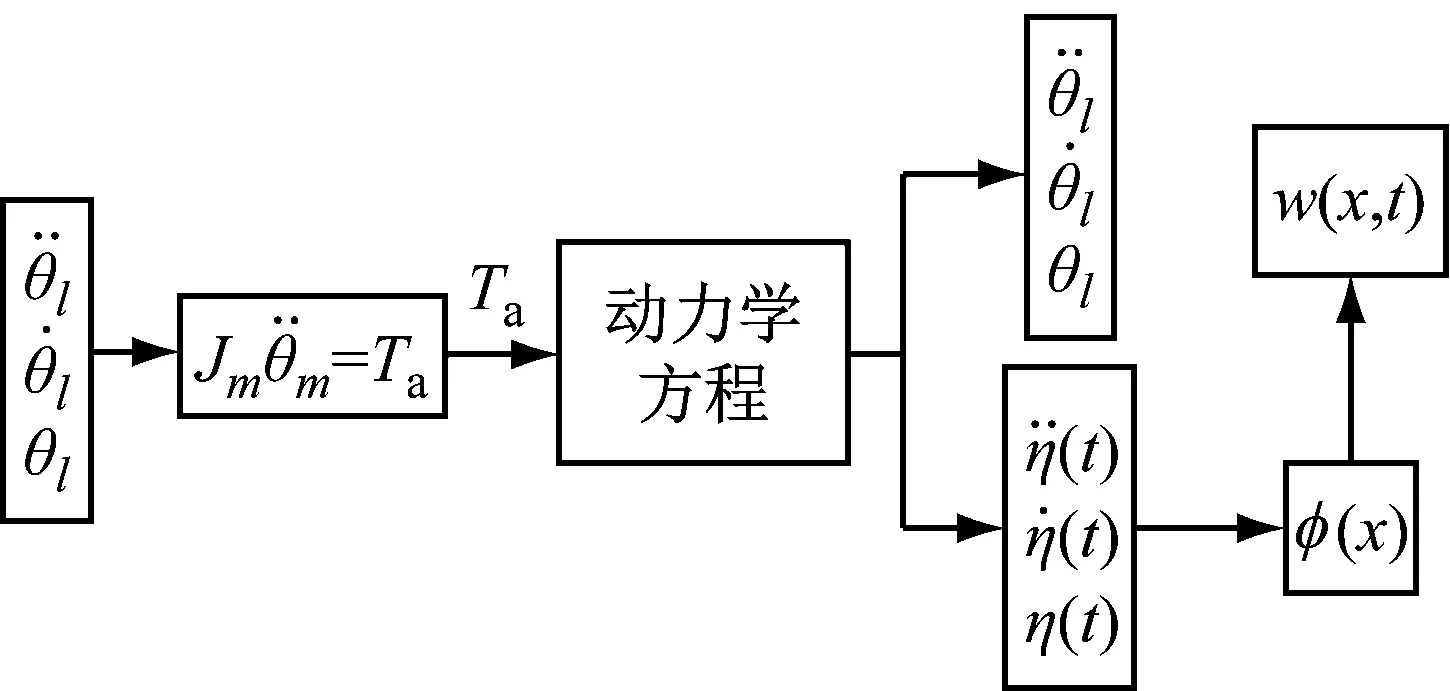
图2 基于角度相关法的柔性结构变形计算流程Fig.2 Calculation flows of the flexible structure deformation based on angle correlation method

为了说明不同物理参数对于空间柔性机械臂变形的影响规律,本文分析不同柔性结构长度和抗弯刚度对于变形的影响。根据式(10)、式(13)和式(14)可得到考虑二维变形、考虑一维变形、忽略耦合非线性项情况下柔性结构的末端变形,如图3所示。

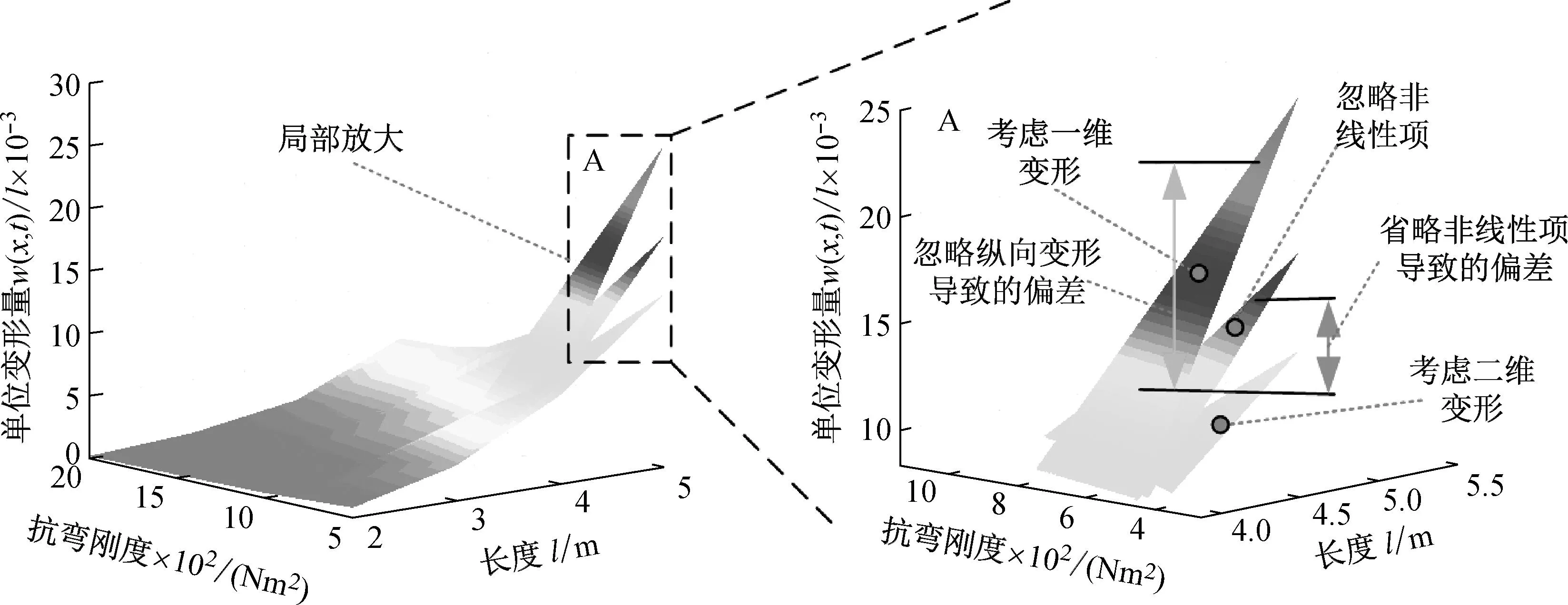
(a) 柔性结构变形分布图

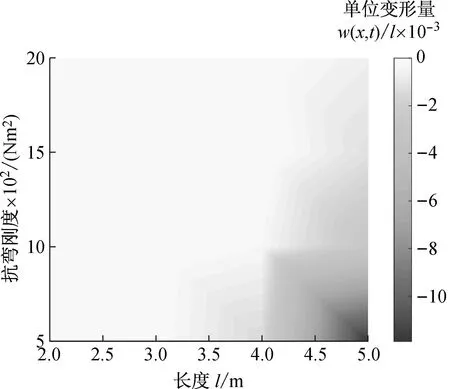
(b) 考虑一维因素的偏差

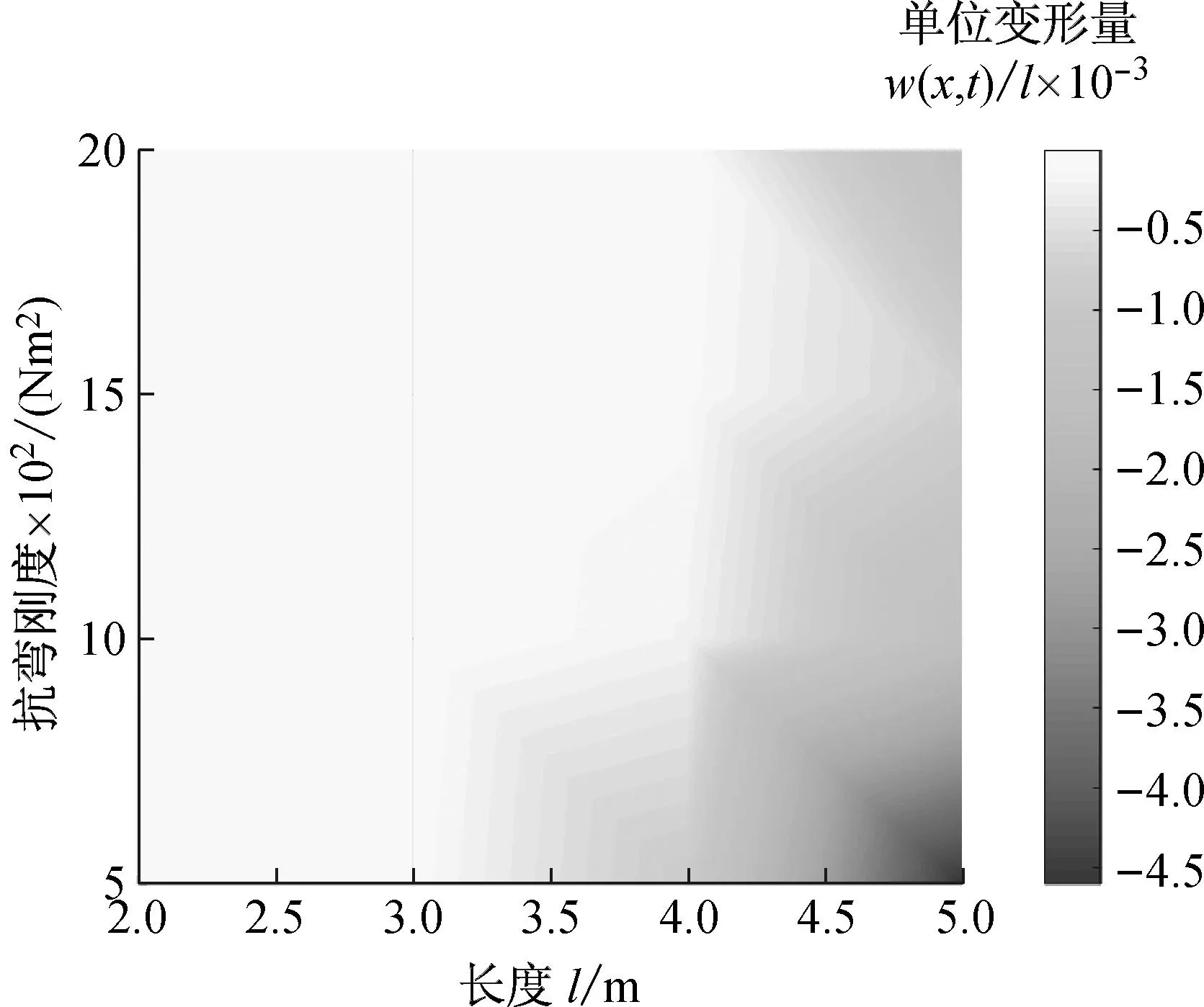
(c) 忽略非线性项的偏差图3 柔性结构的变形Fig.3 Deformation of flexible structure

根据图3可知,在柔性结构长度较小且抗弯刚度较大的情况下,耦合非线性项等对于变形量影响不大。但在柔性结构长度较长且抗弯刚度较小的情况下,耦合非线性项对于变形量有很大的影响。一般认为考虑非线性因素越多,建模精度越高。因此,考虑二维变形的动力学模型具有较高的建模精度。根据图3可知,去除非线性项的动力学模型获得的变形分布与考虑二维变形的动力学模型所得到变形分布规律更为接近。由此可以说明,去除非线性项的动力学模型具有较高的建模精度。

3 模糊补偿滑模控制策略

虽然去除非线性项的动力学模型便于计算且具有较高的建模精度,但是仍和真实的模型之间存在较大的建模误差。本文通过模糊规则辨识、补偿这种建模误差,进而提高空间柔性机械臂的控制精度。

将式(14)所示的空间柔性机械臂的动力学方程写成矩阵的形式,如式(18)所示

(18)

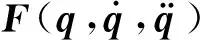
3.1 模糊规则的万能逼近特性

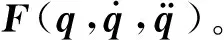
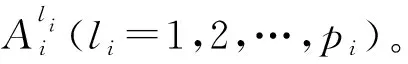
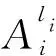
(19)

式中:li=1,2,…,pi,i=1,2,…,n。模糊系统的输出如式(20)所示

(20)

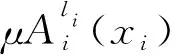
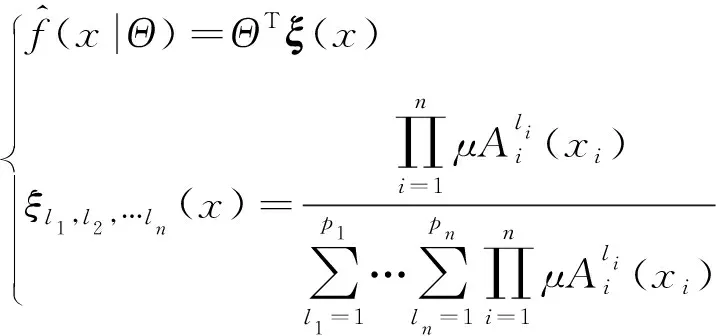
(21)

使用高斯函数作为隶属度函数,如图4所示。

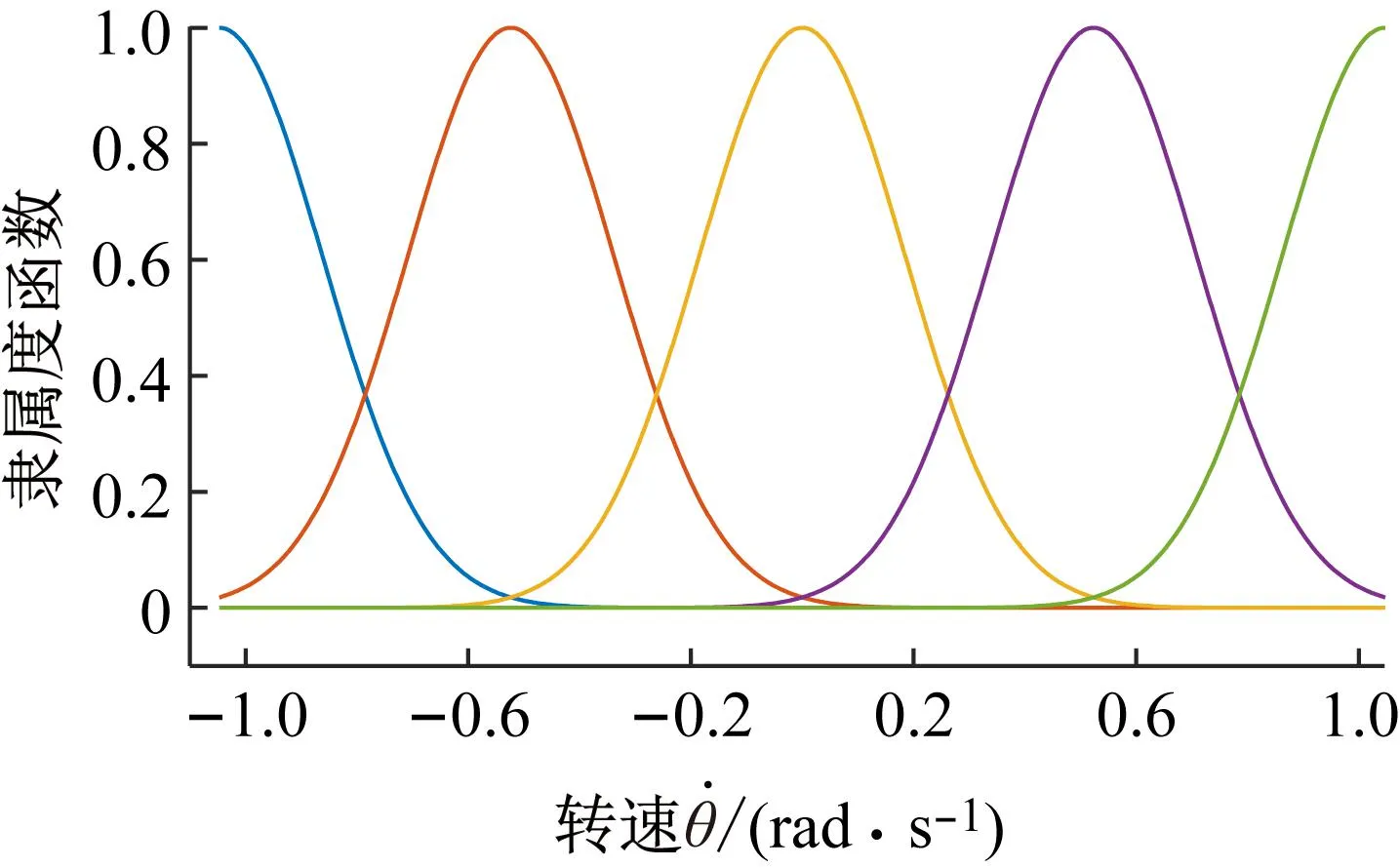
图4 高斯隶属度函数Fig.4 Gaussian membership function

本文使用模糊规则辨识不确定成分。根据式(21)辨识后的不确定成分可以写成式(22)所示的形式。

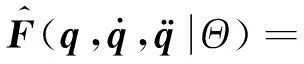
(22)

经过模糊规则辨识后的不确定成分和真实的不确定成分之间仍存在辨识误差,如式(23)所示。

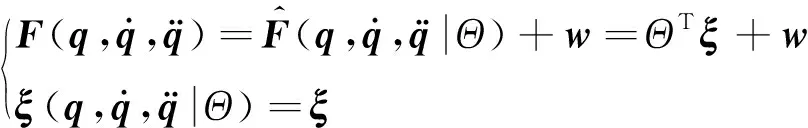
(23)

3.2 控制律和自适应律的设计

定义滑模函数的表达式如式(24)所示

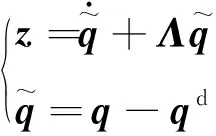
(24)

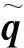
根据式(24)可以得到式(25)

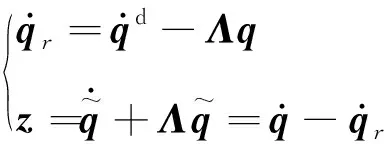
(25)

根据式(18)和式(25)可得到式(26)

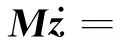
(26)

定义李雅普诺夫函数,如式(27)所示

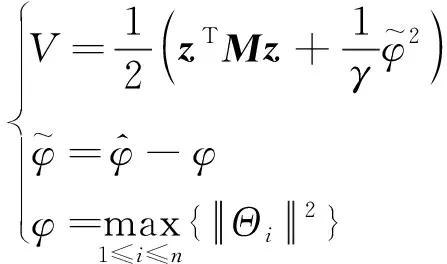
(27)

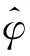
根据式(27)可得到式(28)

(28)

根据式(26)和式(28)可得到式(29)

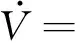
(29)

空间柔性机械臂的控制律设计成如式(30)所示的形式

(30)

式中,KD和W表示控制律参数矩阵。

将式(30)代入式(29)后可得到式(31)

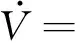
(31)

根据式(27)可得到式(32)

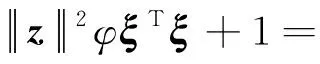
(32)

根据式(32)可得到式(33)

(33)

由此,根据式(33),式(31)可以写成式(34)所示的形式

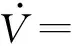
(34)

模糊规则的自适应律设计成如式(35)所示的形式

(35)

式中,α为系数。

将式(35)代入式(34)可得到式(36)

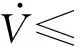
(36)

将式(36)写成式(37)所示的形式

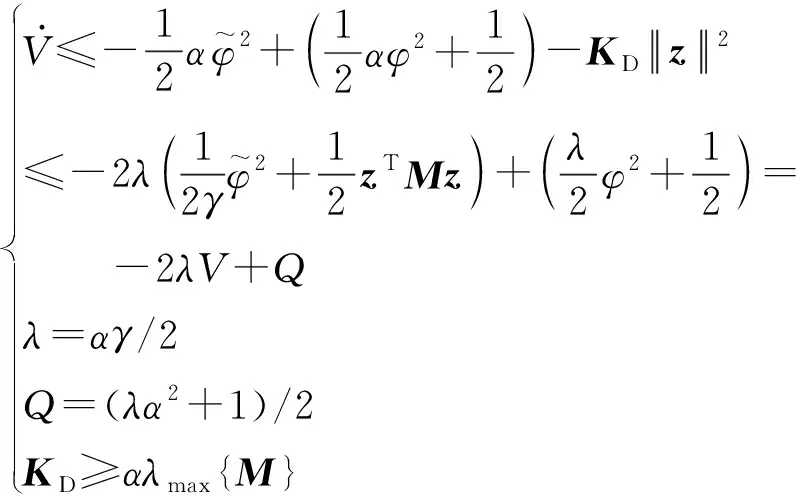
(37)

(38)

对式(38)取极限可以得到式(39)

(39)

根据式(39)可知,V是有界,从而z和φ有界。因此,可以说明本文提出的控制律是能够保证空间柔性机械臂稳定的。使用模糊补偿滑模控制策略的空间柔性机械臂的控制回路,如图5所示。

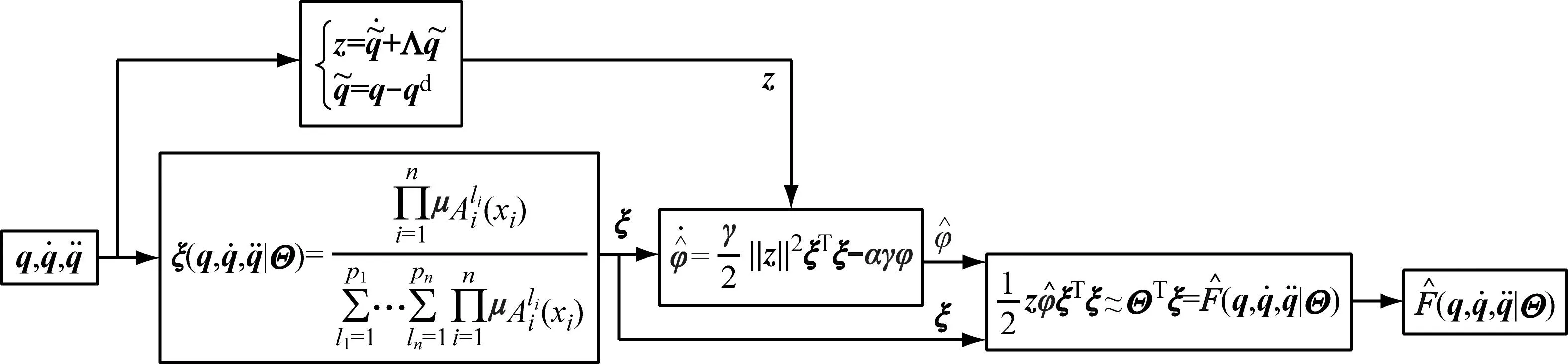
(a) 模糊规则辨识不确定成分流程图

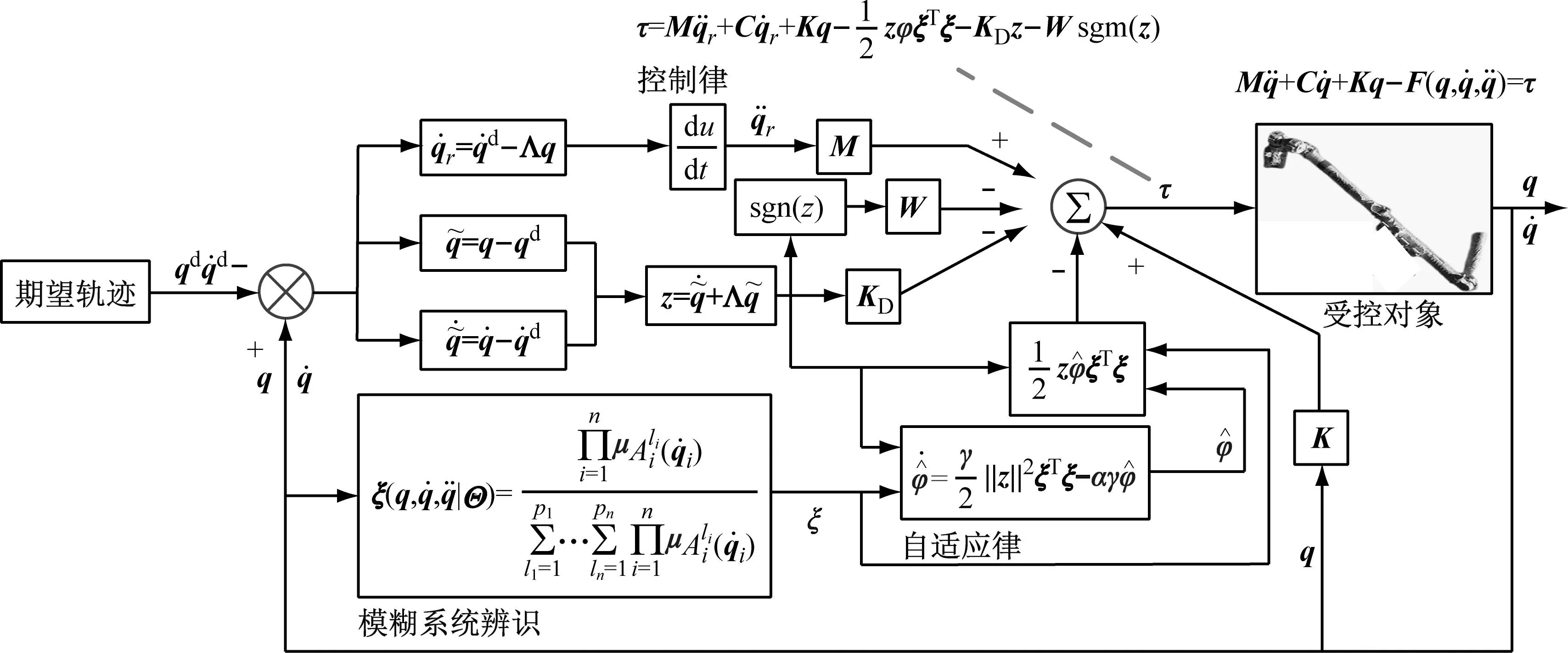
(b) 详细的控制回路图5 基于模糊补偿滑模控制策略的空间柔性机械臂控制回路Fig.5 Control loop of space-flexible manipulator based on fuzzy compensation sliding mode control strategy

4 仿真分析与样机试验

为了说明模糊补偿滑模控制策略对于空间柔性机械臂转动控制和振动抑制的有效性,本文开展了仿真和样机控制试验。首先搭建了模拟空间柔性机械臂的地面控制试验平台,如图6所示。

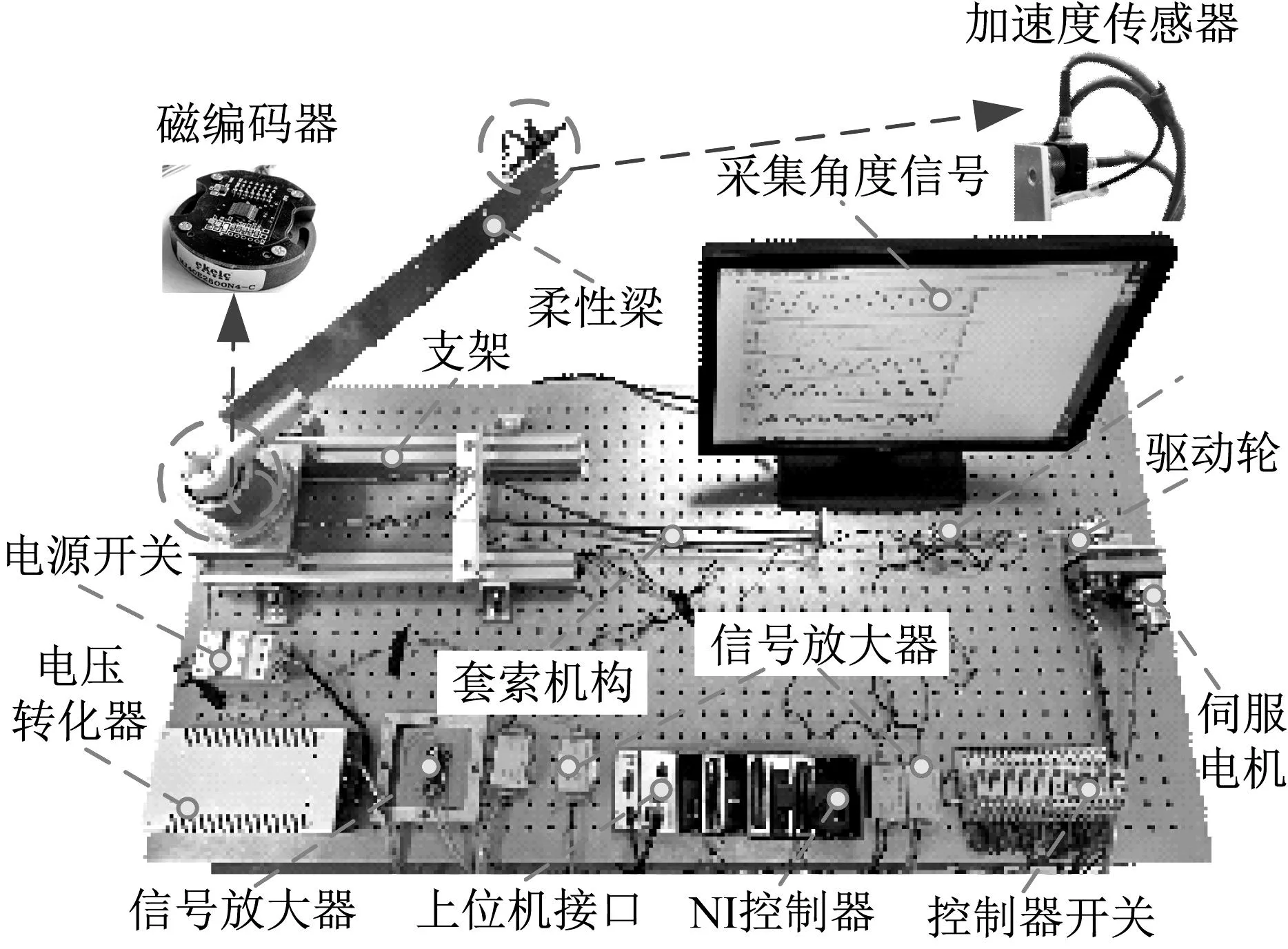
图6 模拟空间柔性机械臂的地面控制试验平台Fig.6 Ground control test platform simulating space-flexible manipulator

试验平台由伺服电机、套索传动机构、柔性梁、NI控制器、磁编码器和加速度传感器等组成。其中,伺服电机的型号为ASME-MRB。NI控制器由NI- Crio -9053模块、NI-9401模块和NI-9264模块组成。控制力矩通过伺服电机传递到套索传动机构,进而驱动柔性梁转动。柔性梁的转角信号由编码器采集后传输到NI-9401模块,然后进入控制程序。控制程序根据实时旋转角度信号计算控制转矩。NI-9264产生脉冲信号,实时调节伺服电机转矩。柔性梁的加速度信号由DH311E型号的加速度传感器测得。其中,样机控制试验平台的控制原理如图7所示。

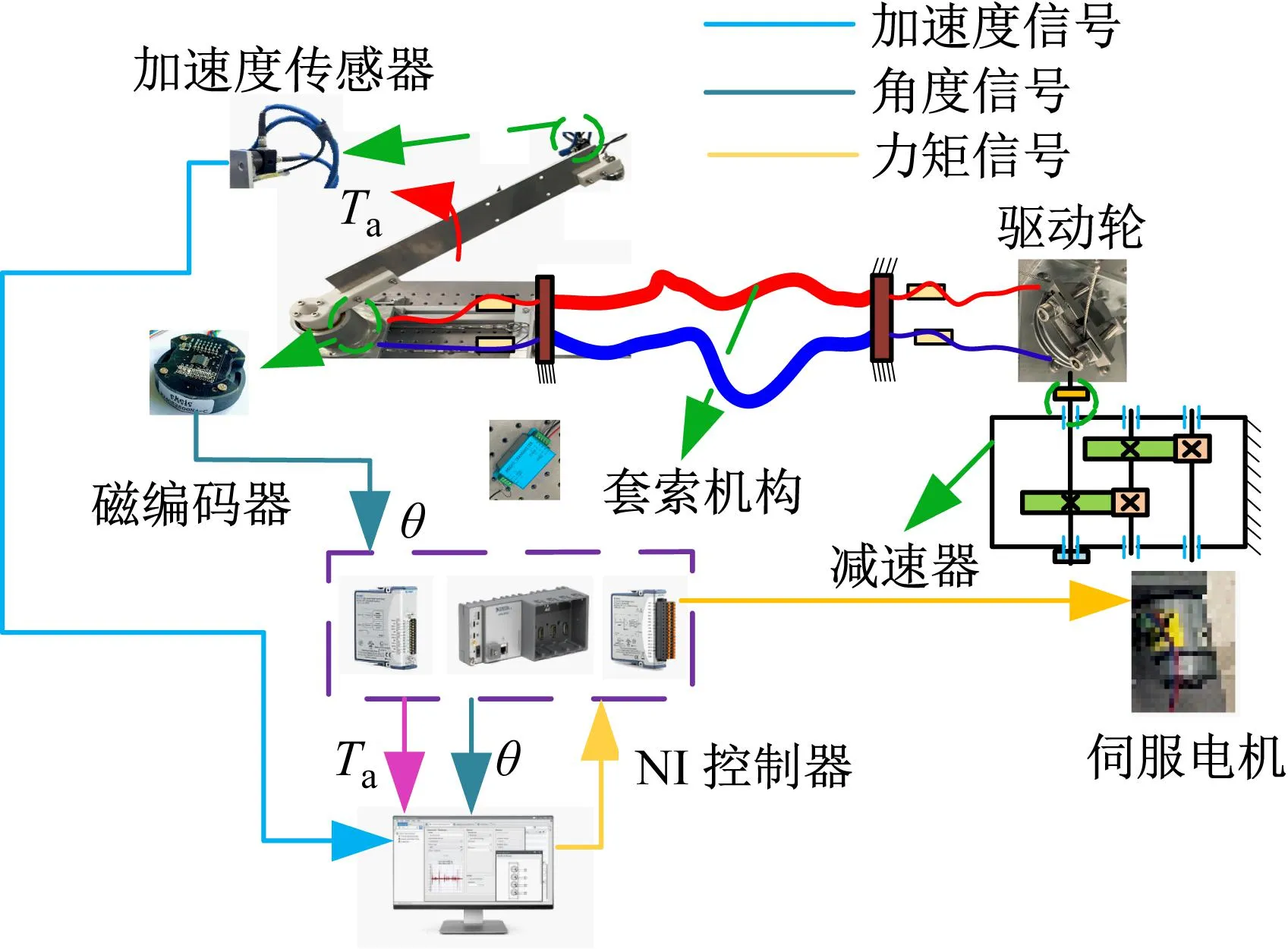
图7 样机控制试验平台的控制原理图Fig.7 Control schematic diagram of prototype control test platform

在仿真分析和样机控制试验中选择两组不同长度的柔性梁进行试验,以此模拟不同长度的空间柔性机械臂。仿真分析和样机控制试验中试验平台的参数如表1所示。

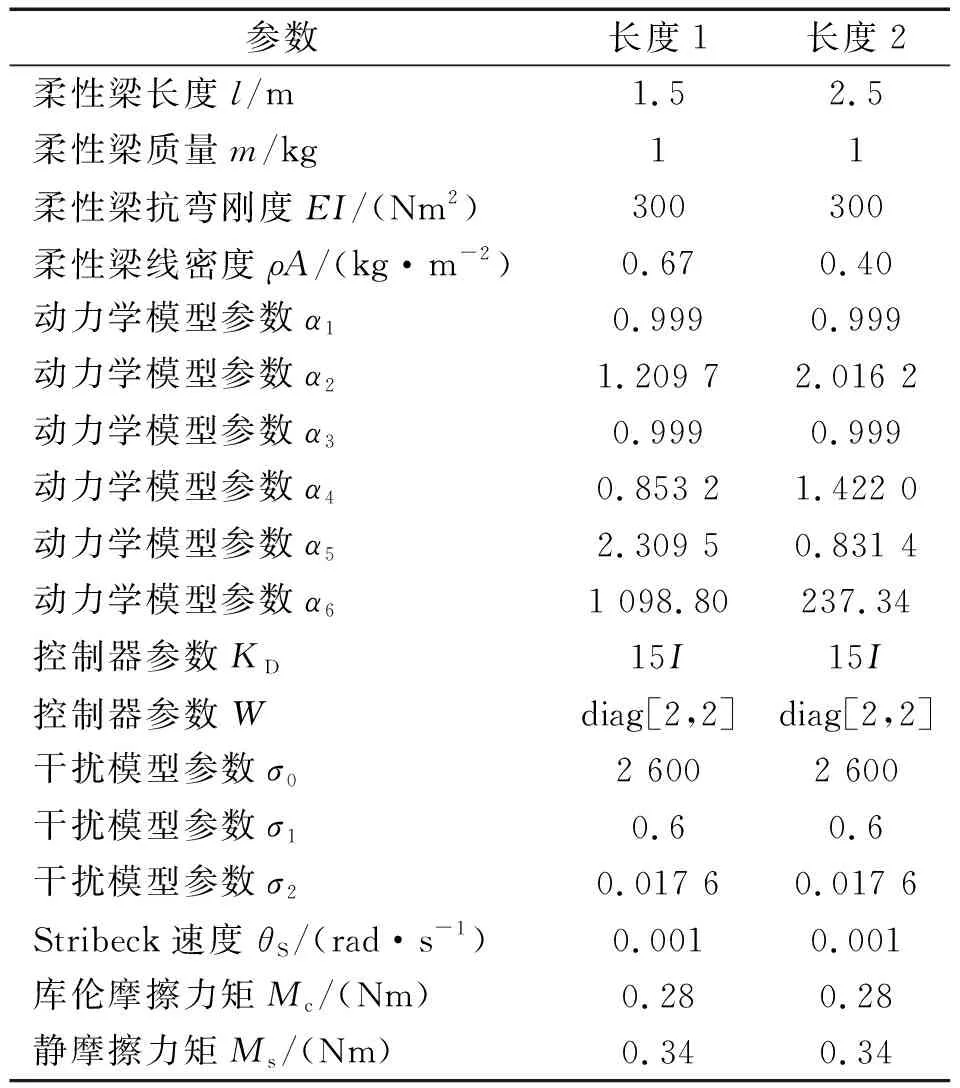
表1 样机控制试验平台参数Tab.1 Prototype control test platform parameters

4.1 数值仿真分析

本文通过数值仿真分析说明所提出的模糊补偿控制策略的有效性。根据表1中的参数开展仿真分析试验。在仿真试验中空间柔性机械臂的期望转速设置为单位正弦信号。分别以滑模控制策略(SMC)和模糊补偿的滑模控制策略(FC+SMC)开展仿真试验。由此,可以得到两种不同柔性结构长度下的仿真结果,如图8～10所示。其中,图8表示转角的仿真试验结果;图9表示转速的仿真试验结果;图10表示柔性变形的仿真结果。

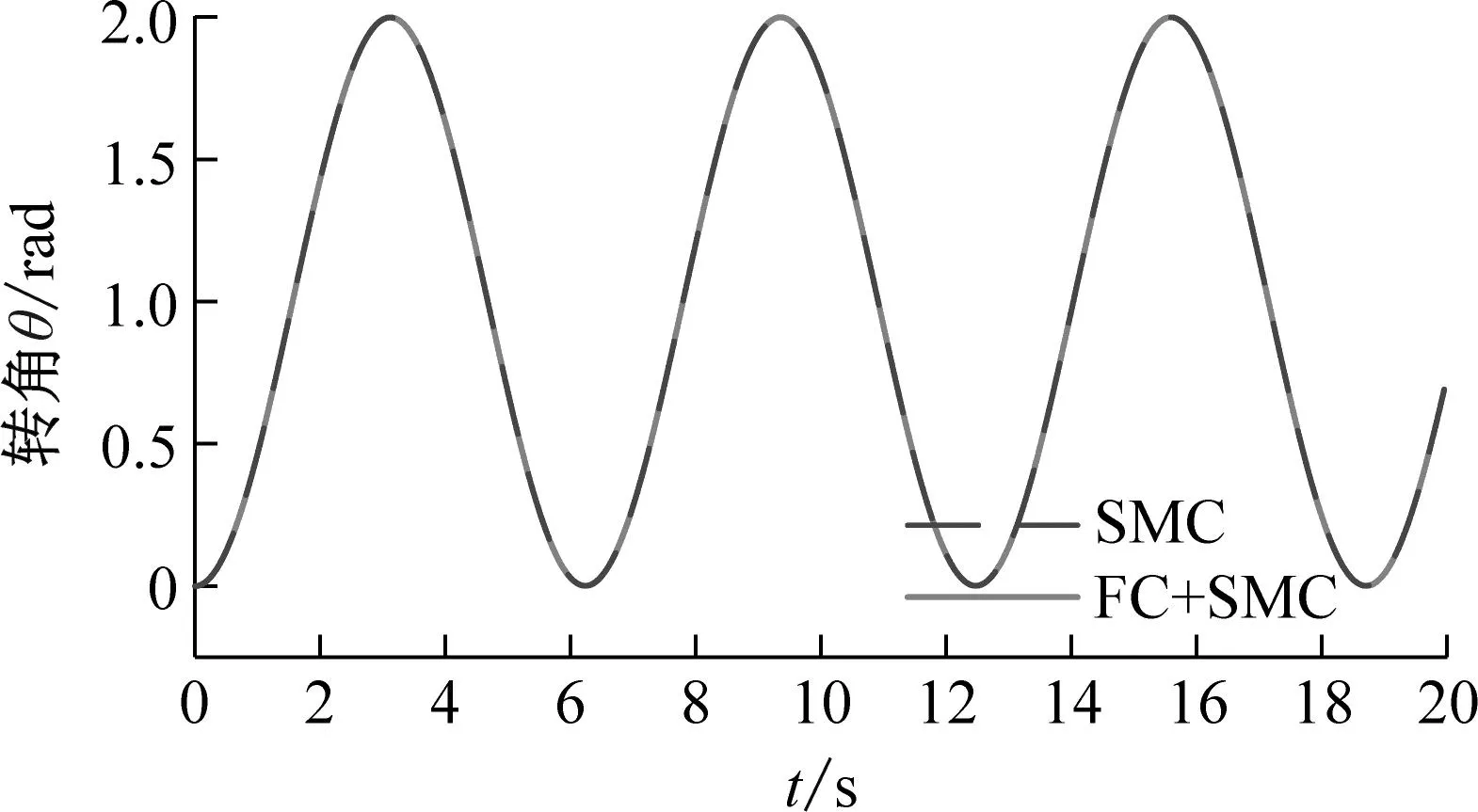
(a) 长度1工况下的转角曲线

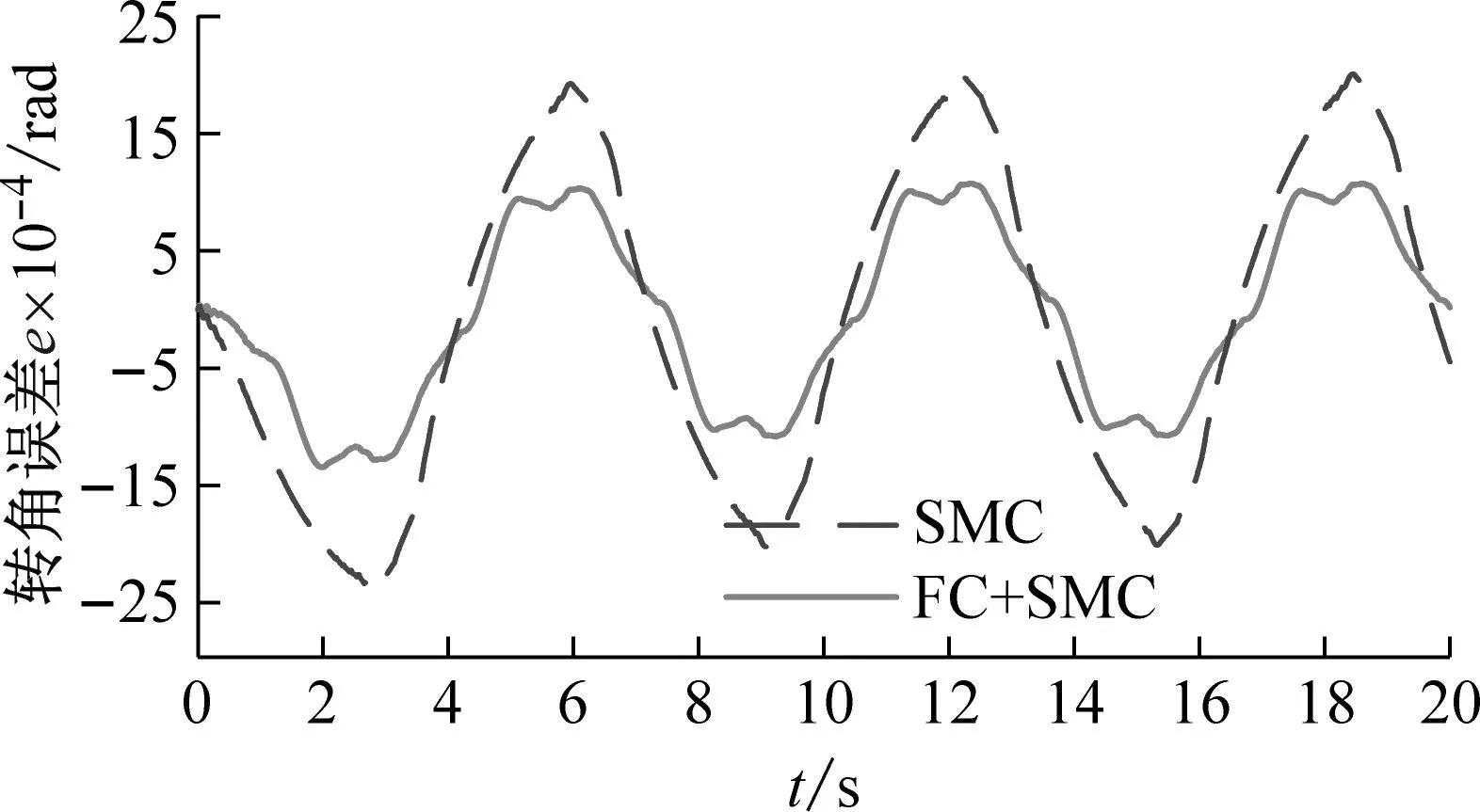
(b) 长度1工况下的转角误差曲线

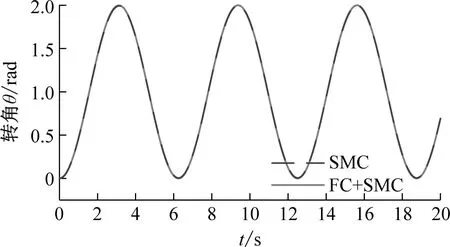
(c) 长度2工况下的转角曲线

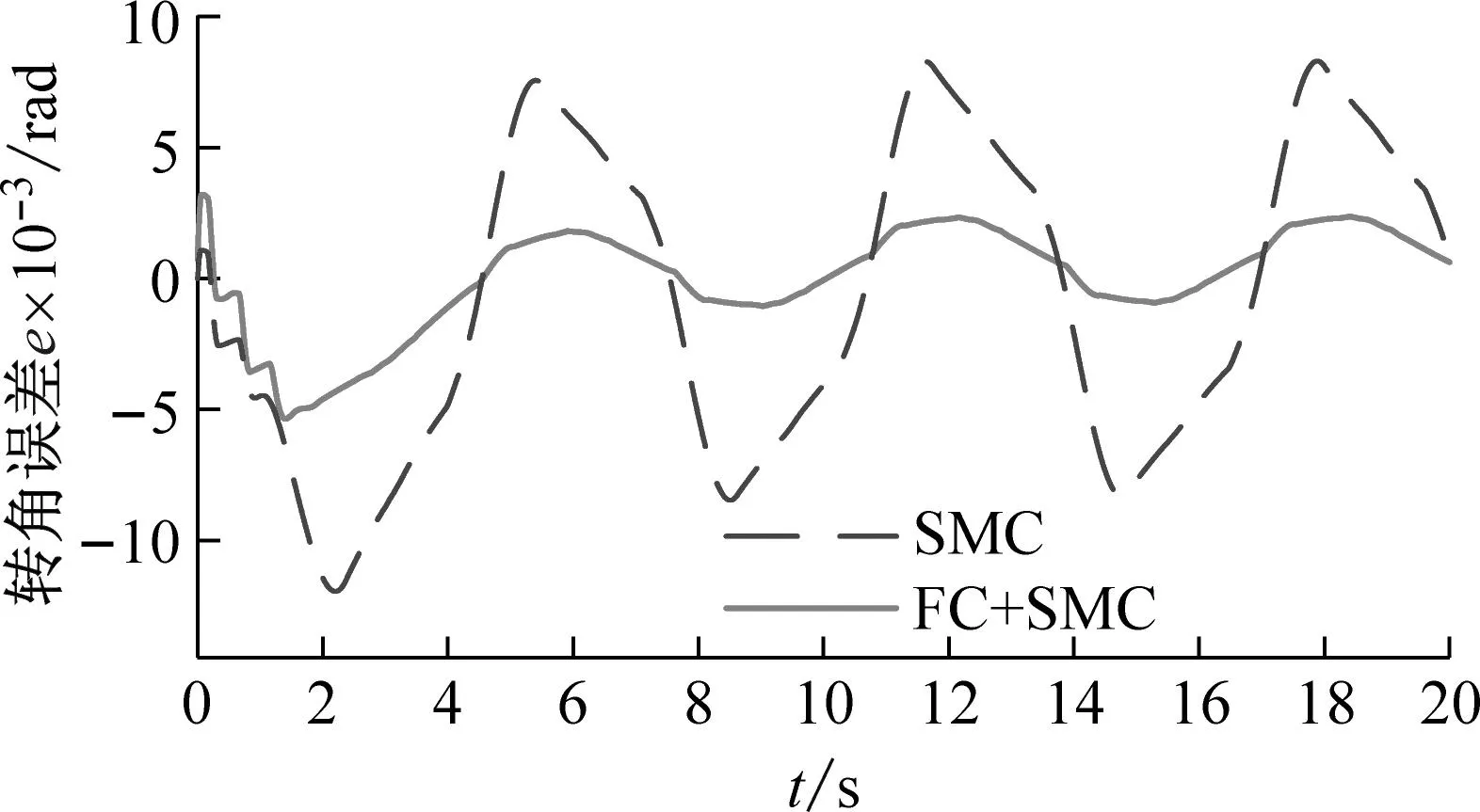
(d) 长度2工况下的转角误差曲线图8 转角仿真试验结果Fig.8 Simulink results of rotation angle

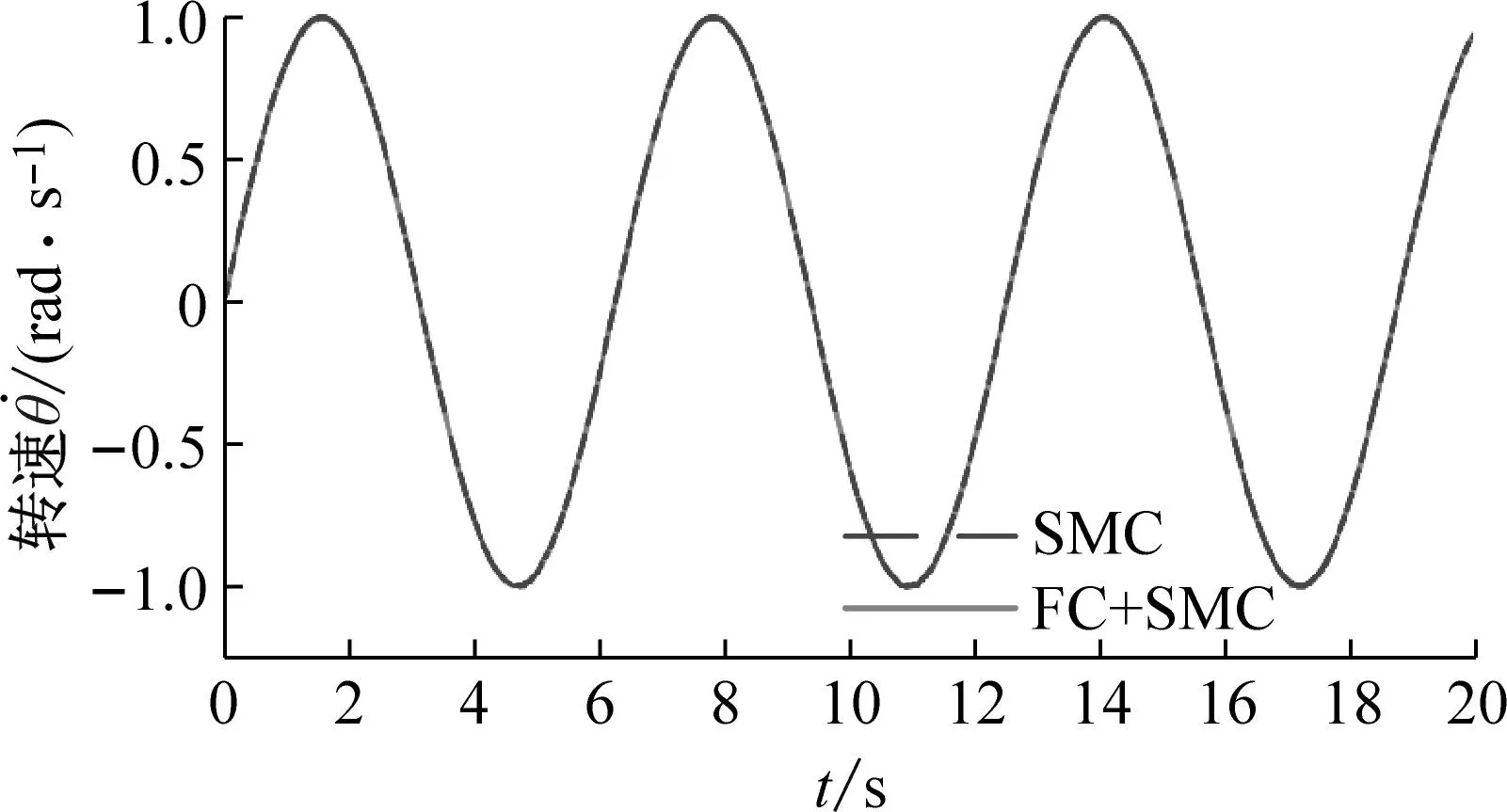
(a) 长度1工况下的转速曲线

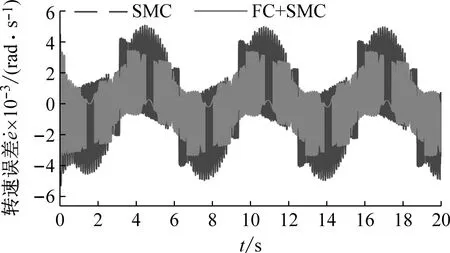
(b) 长度1工况下的转速误差曲线

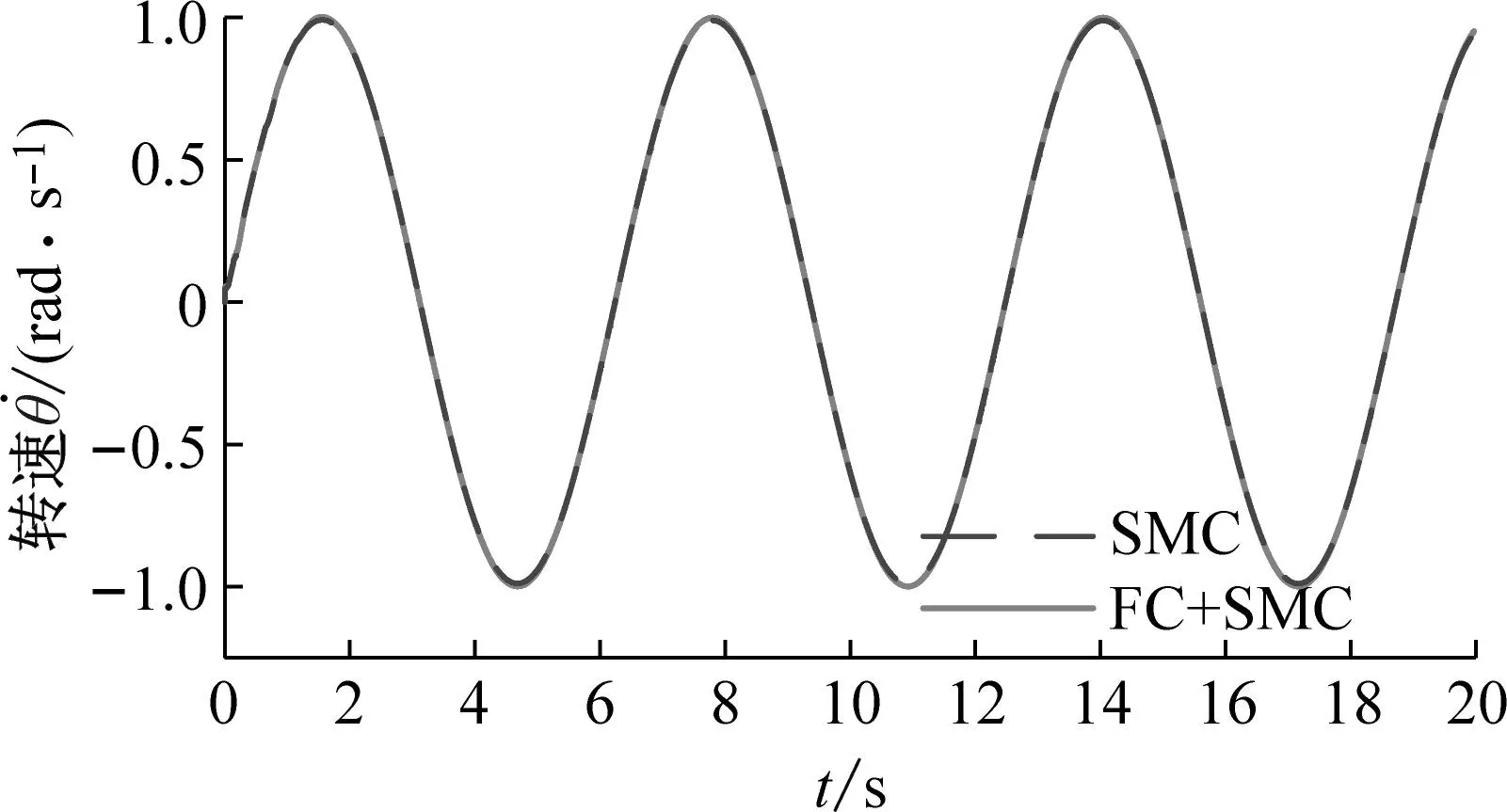
(c) 长度2工况下的转速曲线

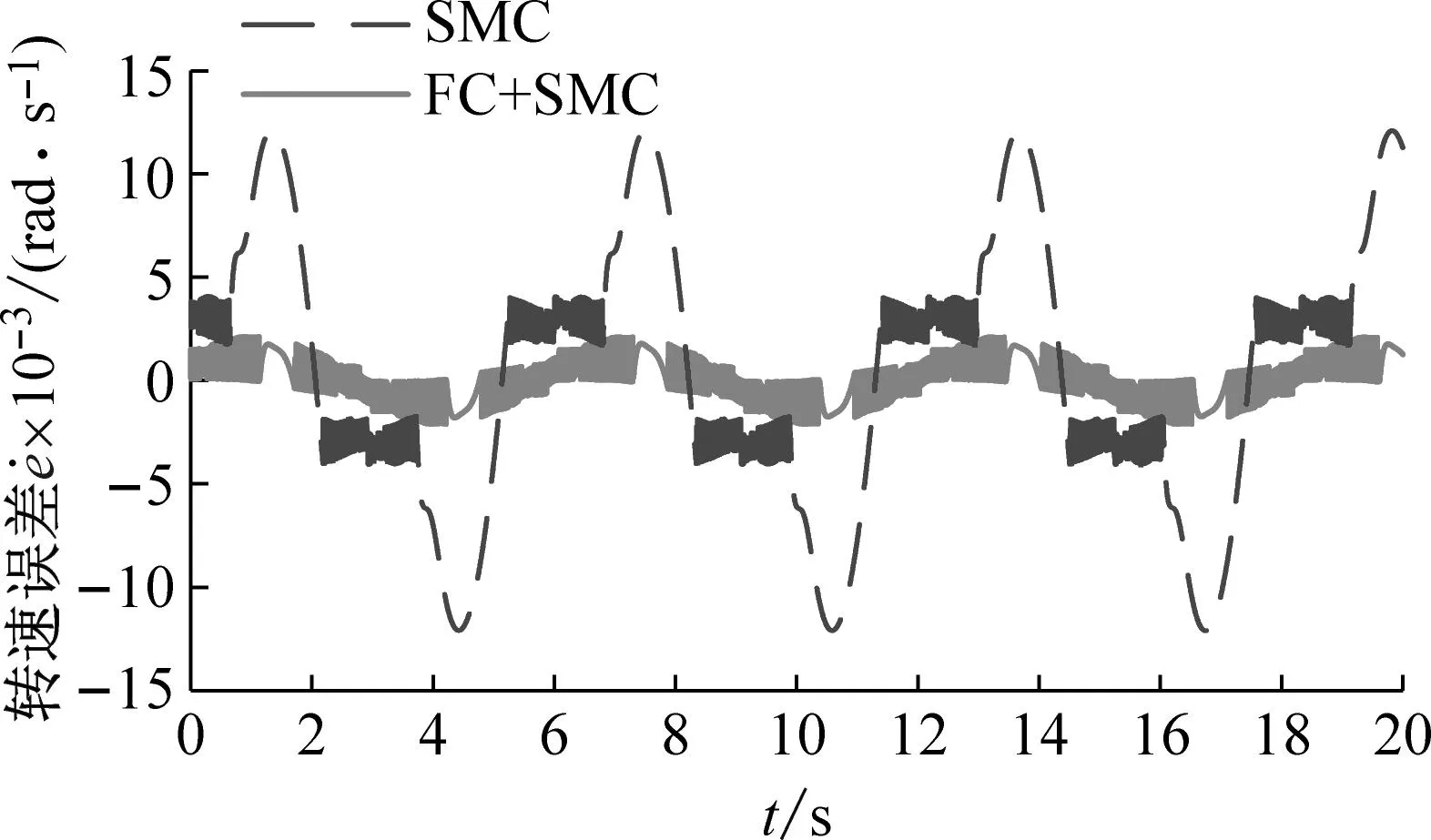
(d) 长度2工况下的转速误差曲线图9 转速仿真试验结果Fig.9 Simulink results of rotation speed

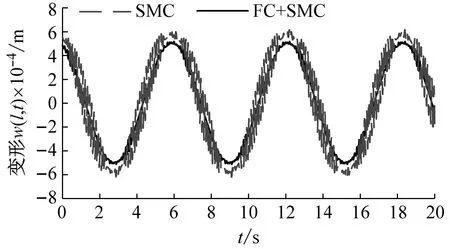
(a) 长度1工况下的变形曲线

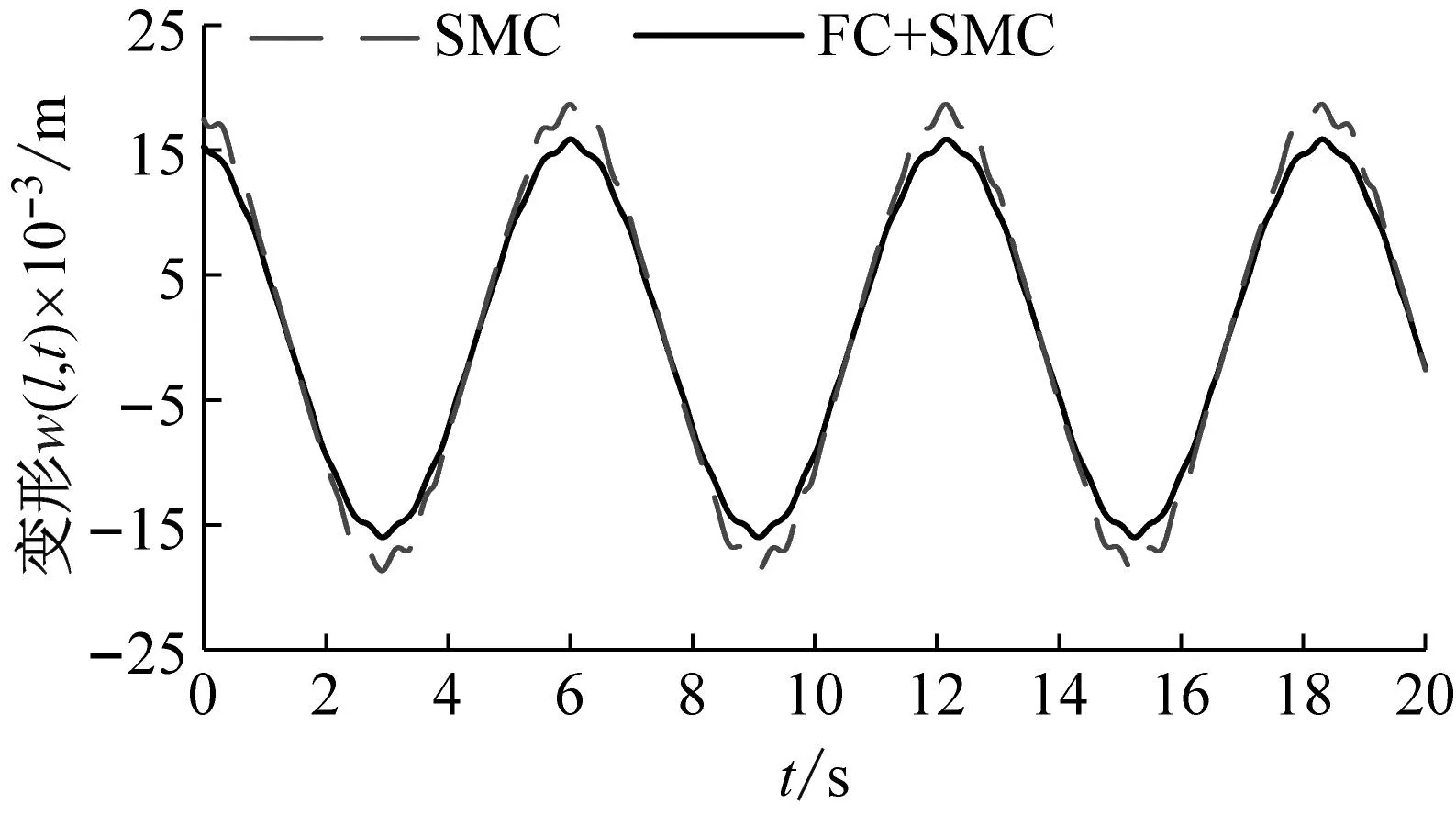
(b) 长度2工况下的变形曲线图10 变形仿真试验结果Fig.10 Simulink results of deformation

根据图8可知,两种控制策略都可以使空间柔性机械臂实现稳定的角度跟踪。并且随着柔性结构长度的增大,转角跟踪误差逐渐增大。但是,与滑模控制策略相比,模糊补偿的滑模控制策略具有更小的转角跟踪误差。相似的,根据图9可知,虽然两种控制策略都能实现稳定的转速跟踪,但是模糊补偿的滑模控制策略具有较小的转速跟踪误差。在柔性结构长度较短的工况下,模糊补偿滑模控制策略的优势更加明显。这是因为当柔性结构长度较小时,受控对象的转动惯量较小,外界干扰对于转速的影响较大。而模糊补偿的控制策略能够消除外界干扰的影响。由此,在柔性结构长度较小的情况下,模糊补偿控制策略的优势更加明显。根据图10可知,在两种不同长度的工况下,模糊补偿滑模控制策略能够减弱变形的幅值。在长度1的工况下,模糊补偿滑模控制策略能够减弱变形曲线的波动。由此可知间接的说明,使用模糊补偿滑模控制可以减弱柔性结构的振动。

根据数值仿真试验所获得的结果可知,与滑模控制策略相比,模糊补偿滑模控制策略可以大幅度地提高空间柔性机械臂的控制精度。空间柔性机械臂的振动抑制效果可以从变形的幅值和波动的减弱间接地体现出来。此外,模糊补偿滑模控制策略通过减弱转速的波动间接的抑制空间柔性机械臂的振动。

4.2 样机控制试验

根据表1中的参数设置物理样机控制试验平台中柔性梁。分别使用模糊补偿滑模控制策略和滑模控制策略开展控制试验。与仿真试验相同,柔性梁的期望转速设置为正弦信号。利用安装于柔性梁末端的加速度传感器收集转动过程中的加速度信号。由于柔性梁的振动幅值难以测量,本文使用加速度信号间接地表征振动强弱。物理样机的试验结果,如图11和图12所示。

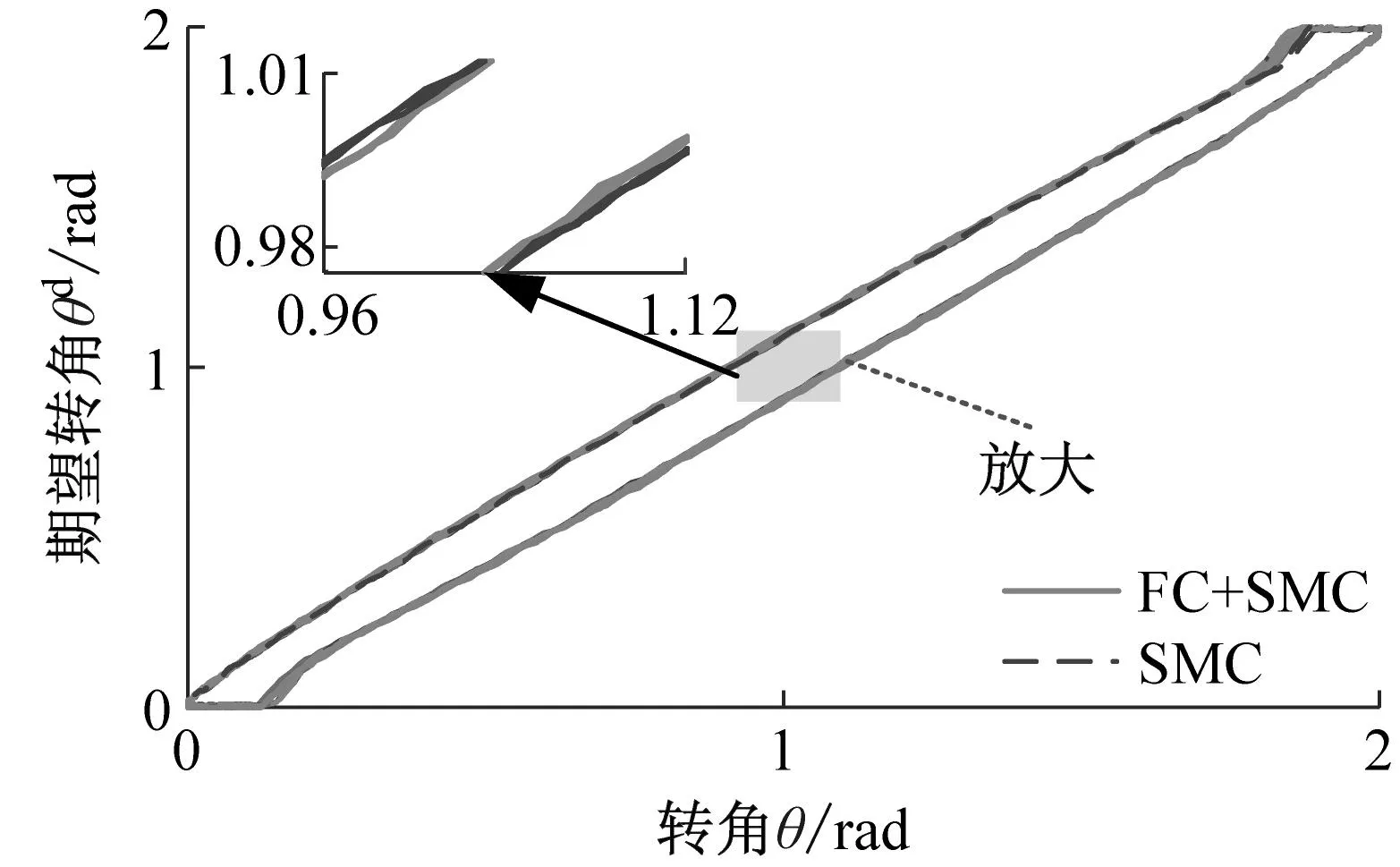
(a) 转角输入输出曲线

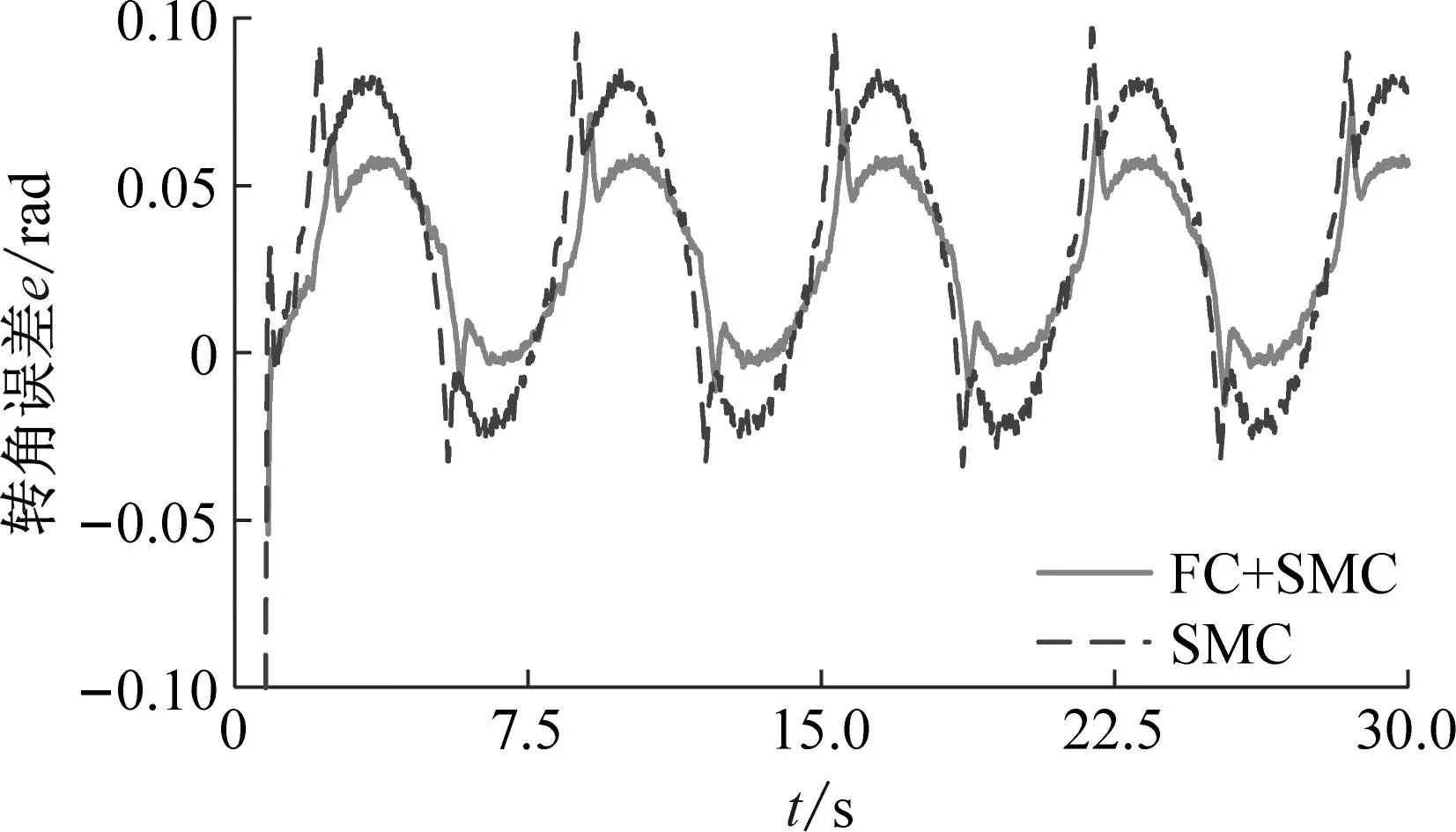
(b) 转角跟踪误差曲线

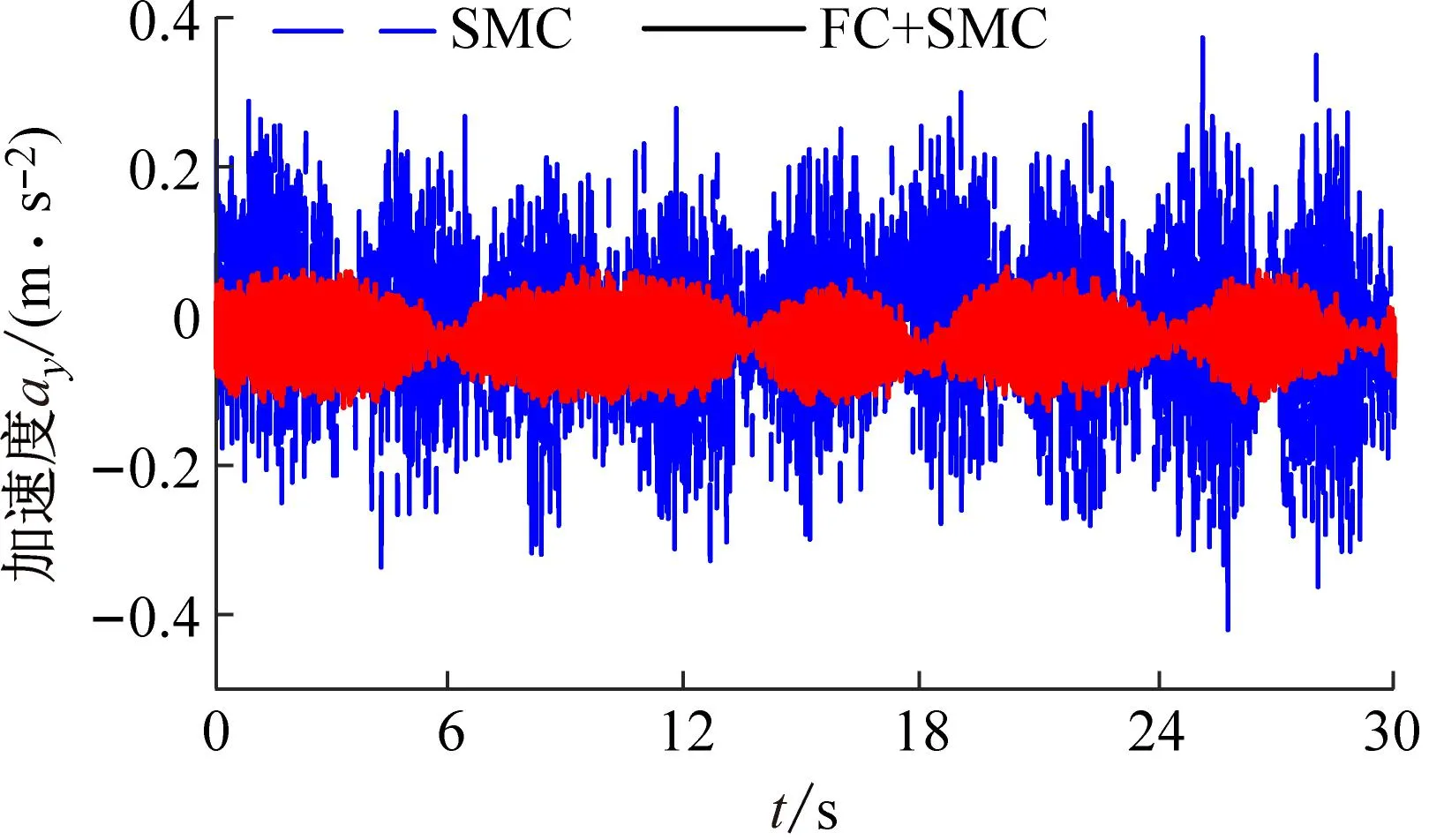
(c) 加速度曲线

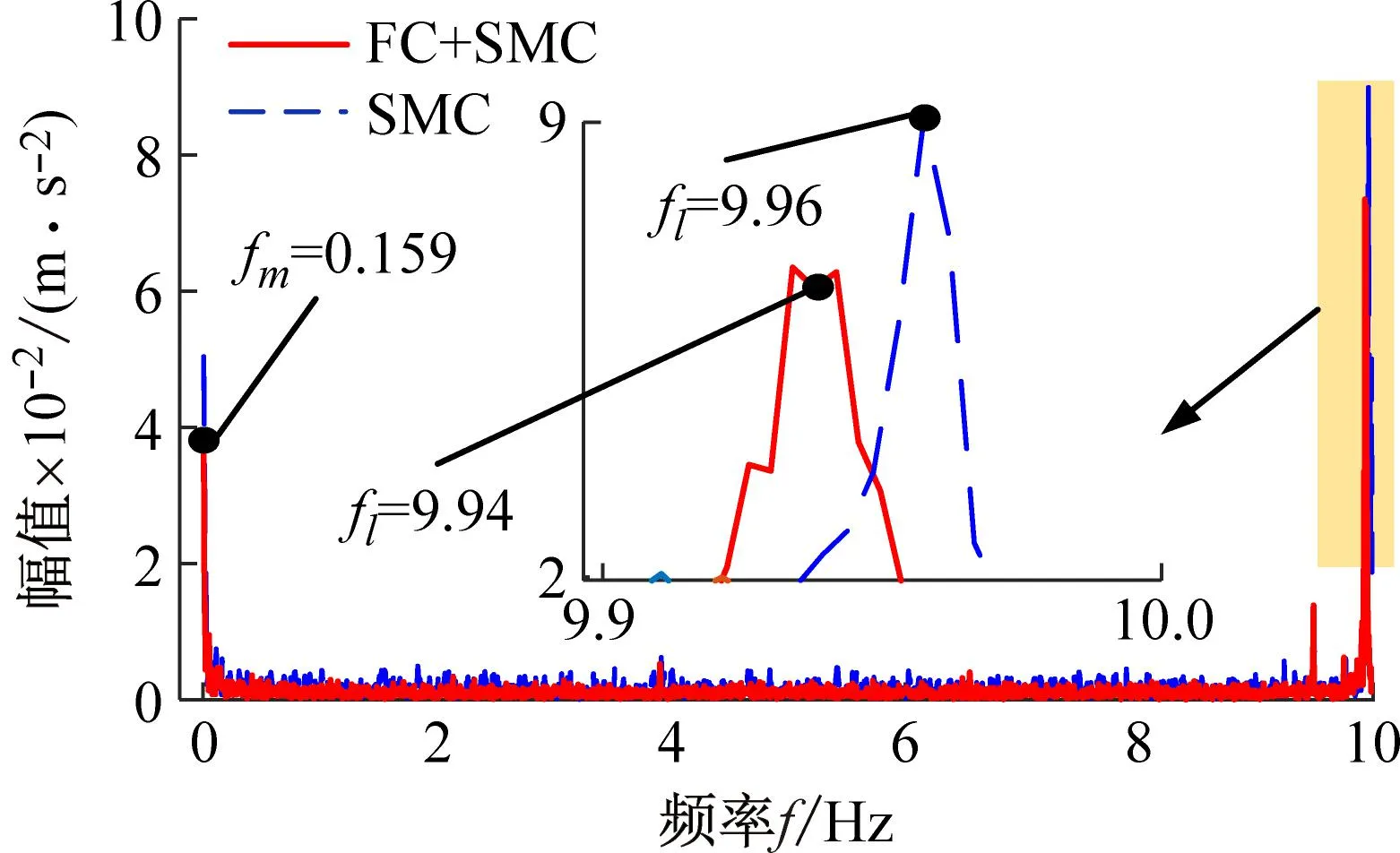
(d) 加速度分率分布图11 长度1工况下试验结果Fig.11 Test results under the condition of length 1

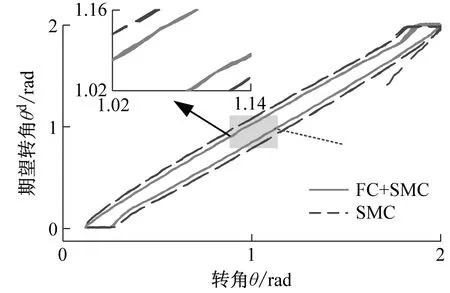
(a) 转角输入输出曲线

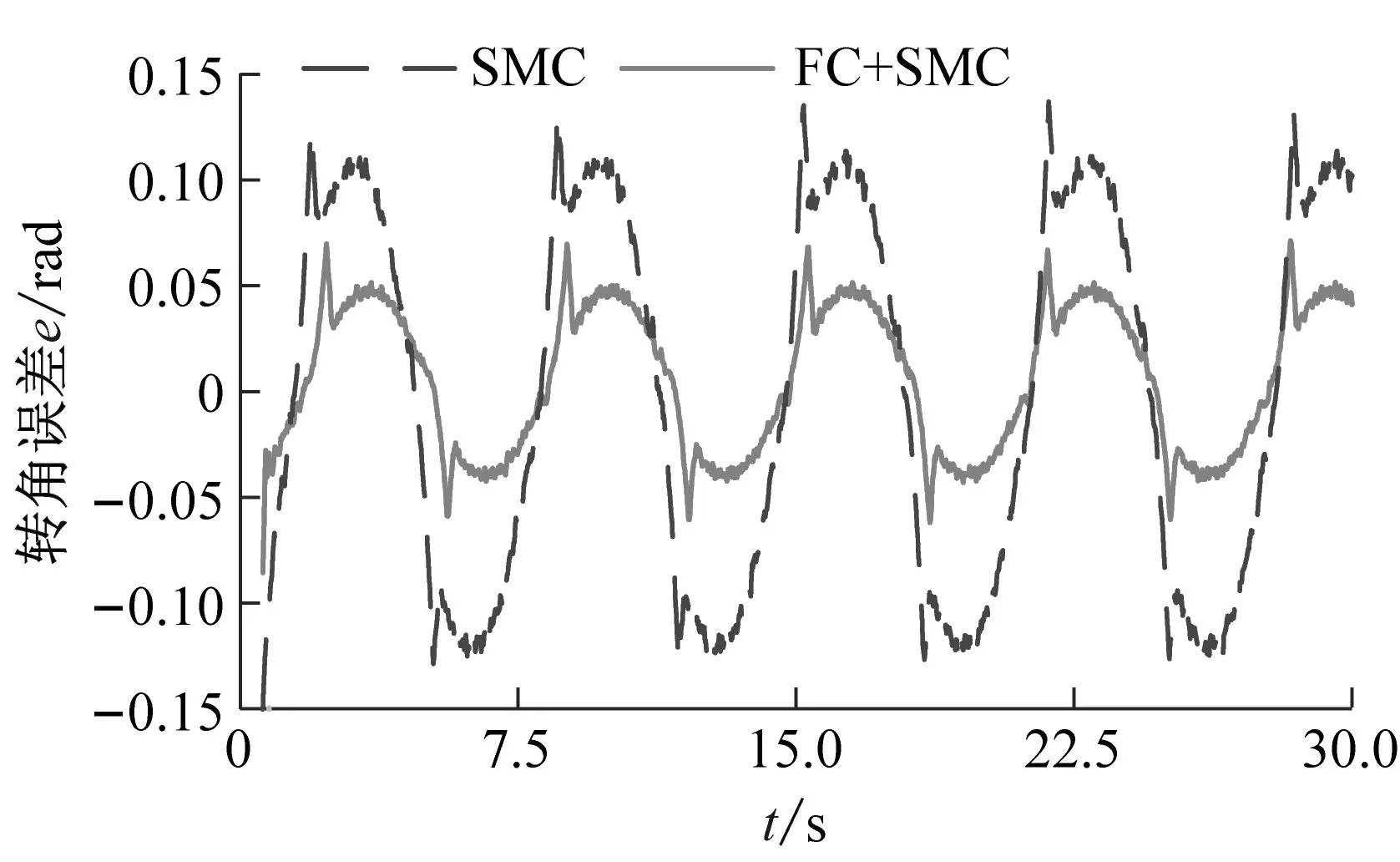
(b) 转角跟踪误差曲线

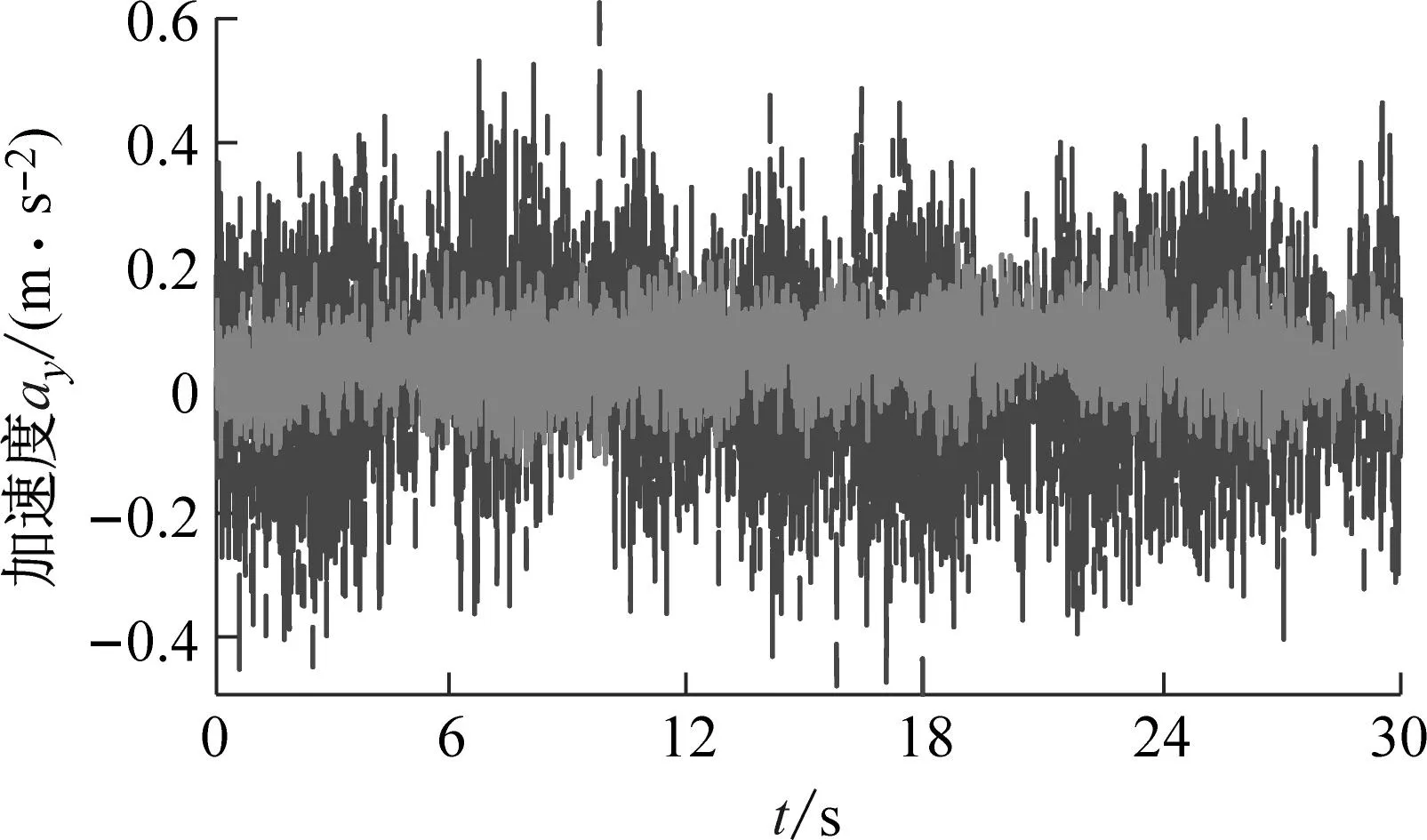
(c) 加速度曲线

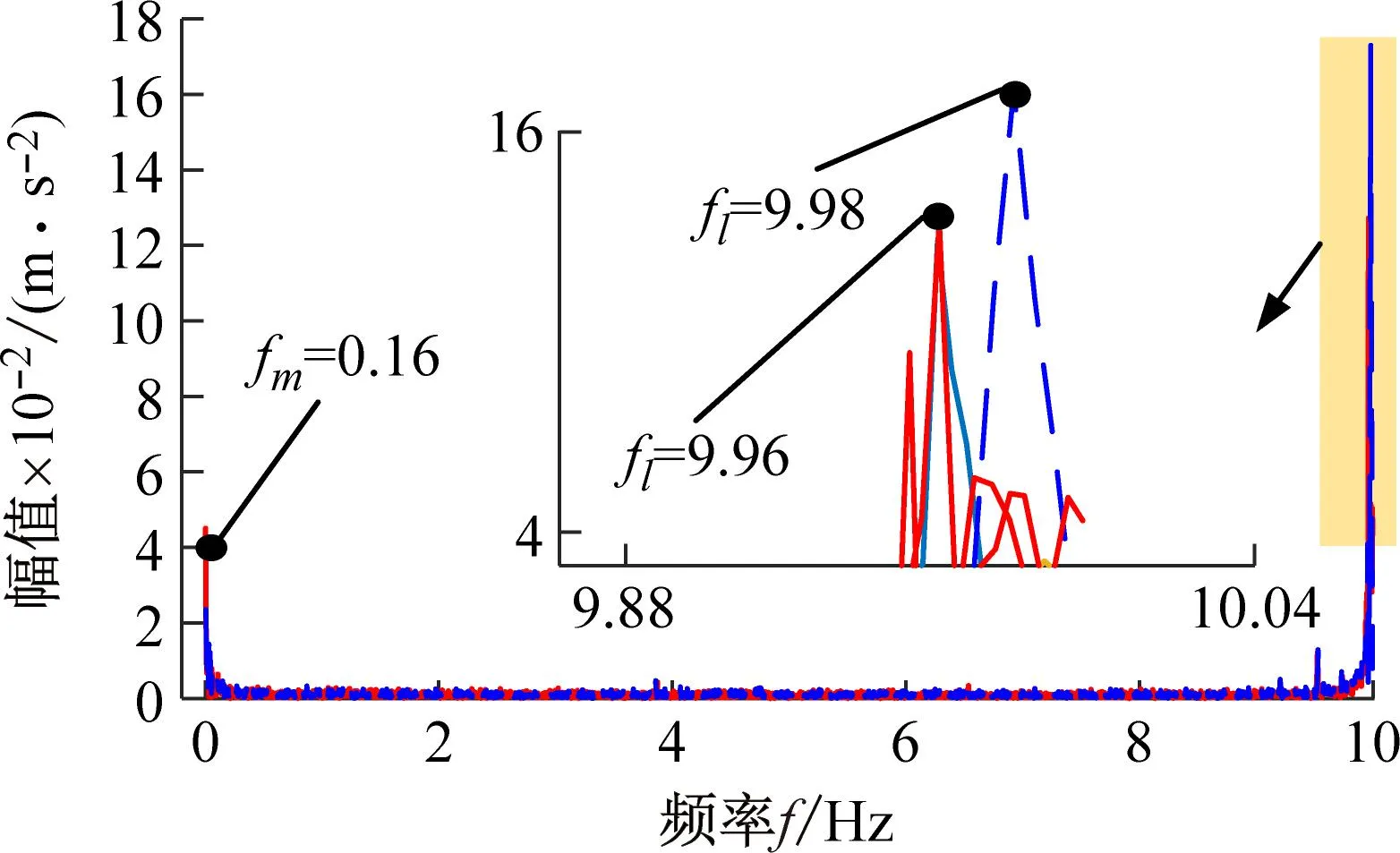
(d) 加速度分率分布图12 长度2工况下试验结果Fig.12 Test results under the condition of length 2

根据图11和图12可知,随着柔性梁长度的增加,转角误差和加速度信号的幅值逐渐增加。但是,模糊补偿滑模控制策略却可以有效地减弱柔性梁的跟踪误差和加速度幅值。此外,从图11中加速度信号的傅里叶变换结果可以看出,柔性梁在旋转过程中有两个主要频率。其中一个是主频处于低频区域与柔性梁旋转频率相对应,另一个主频处于高频区域与柔性梁的振动频率相对应。两种不同的控制策略对柔性梁的频率的影响有限。这表明模糊补偿滑模控制策略可以在不改变运动特性的情况下提高柔性梁的运动精度。

为了更加清晰地说明模糊补偿控制策略的优势,本文对转角跟踪误差和加速度数据进行统计学分析。由此可以得到跟踪误差和加速度信号的统计指标分布规律,如图13所示。

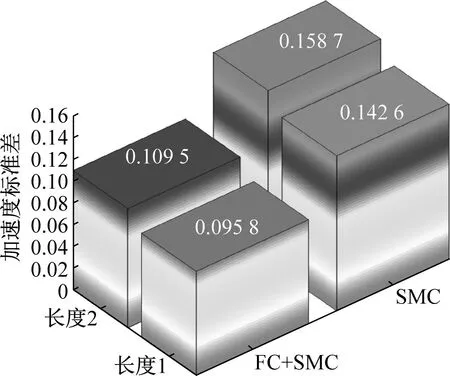
(b) 加速度标准差指标图13 试验数据统计指标分布图Fig.13 Test data statistical index distribution map

根据图13可知,在两种长度工况下,模糊补偿滑模控制策略都具有最好的统计指标。相比较于滑模控制策略,模糊补偿滑模策略可以使转角跟踪误差绝对值的平均值下降17.86%、加速度的标准差下降31.90%。试验数据的量化分析结果再一次的证明了滑模控制策略的有效性和优势。

综上,根据数值仿真分析和样机控制试验说明了模糊补偿滑模控制策略可以有效地提高空间柔性机械臂的转角控制的精度。进而减弱振动。

5 结 论

本文以空间柔性机械臂为研究对象,建立了考虑二维变形和外界干扰的动力学模型。采用模糊补偿滑模控制策略提高空间柔性机械臂的转动精度,进而减弱振动。模糊补偿滑模控制策略通过模糊规则辨识补偿包含柔性非线性项和外界干扰的动力学不确定成分提高控制精度。仿真分析和样机控制试验表明,所提出的控制策略能有效提高旋转角度的控制精度、减弱振动。具体结论如下:

(1) 空间柔性机械臂的动力学方程包含许多非线性项。当柔性结构长度较长、抗弯刚度较小时,这些非线性项对空间柔性机械臂的建模精度有一定的影响。在动力学建模中应该考虑这些非线性项。

(2)由非线性项和外界干扰组成的不确定部分会影响空间机械臂的转动控制精度。模糊补偿策略可以辨识和补偿动力学模型的不确定成分,从而提高转动控制精度。

(3) 本文提出的模糊补偿滑模控制策略可以有效地提高空间柔性机械臂的转动控制精度、减弱振动。本文提出的控制策略使转角跟踪误差绝对值的平均值下降17.86%,加速度的标准差下降31.90%。

附录A

动力学模型的参数的表达式如下所示。

(A.1)

(A.2)

(A.3)

(A.4)

(A.5)

(A.6)

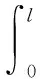
(A.7)