信息智慧转化 基础变式拓展
——以对正四面体与正方体自由旋转的思考为例
李长波 余继光
(1.江苏南京市南京大学附属中学;2.浙江省绍兴市柯桥中学)
将旋转体隐藏在内多面体与外多面体之间,探究它们之间的位置关系与数量关系,成为空间想象能力训练的一个热点,“自由旋转”一词引起学习者思考,什么几何体可以自由旋转呢?只有球体!然而一个多面体在另一个多面体内自由旋转,需要考虑两个球,内多面体的外接球与外多面体的内切球,于是想到如果内多面体的外接球能够放入外多面体的内切球内,就可以实现两个多面体的自由旋转,本文思考正四面体,正方体内放入正四面体或正方体时自由旋转的相关空间位置关系与度量关系问题.
引子:学生面对《浙江新阵地教育联盟2024届高三数学联考》(测试题1)时,遇到一个多面体在另一个多面体内“自由旋转”情境时,由于题干表面是多面体,并不能自由旋转,问题情境中虽然给出“内切球”“外接球”的暗示,但缺少两者的直观想象,空间想象能力较弱者不知将题设问题向何处转化,从而产生思维障碍,学生的思维痛点引发我们的深入思考.
一、“自由旋转”题型审题的基础
1.一个正四面体在另一个正四面体内自由旋转
题型1.一个棱长为a的正四面体A—BCD在另一个棱长为b的正四面体E—FGH内自由旋转
(1)a与b之间的不等关系是什么?
(2)b为定值,a的最大值为多少?
(3)a为定值,b的最小值为多少?

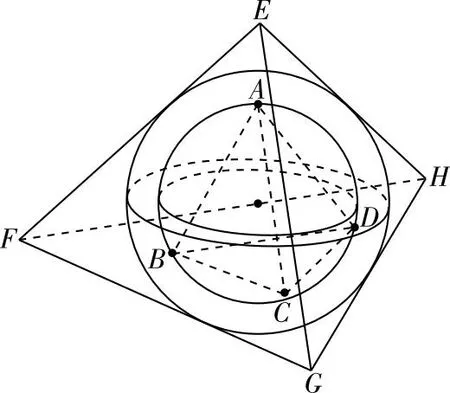
图1

借助于直观图形给学生解读“自由旋转”,正四面体A—BCD在其外接球O1内自由旋转,正四面体E—FGH在其内切球O2外自由旋转,而O1在O2内自由旋转,从而实现正四面体A—BCD在正四面体E—FGH内“自由旋转”.
题型2.两个小正四面体放进一个大正四面体内自由旋转
两个棱长为a的小正四面体A—BCD在另一个棱长为b的大正四面体E—FGH内自由旋转.
(1)a与b之间的不等关系是什么?
(2)b为定值,a的最大值为多少?
(3)a为定值,b的最小值为多少?
【解析】两个小正四面体的外接球放入大正四面体E—FGH的内切球内,才能保证“自由旋转”,设正四面体A—BCD外接球半径为R,正四面体E—FGH内切球半径为r,则2R≤r.
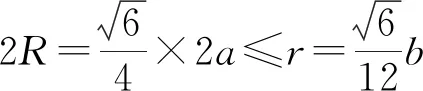
2.一个正四面体在一个正方体内自由旋转
题型1.一个棱长为a的正四面体E—FGH在一个棱长为b的正方体ABCD—A1B1C1D1内自由旋转
(1)a与b之间的不等关系是什么?
(2)b为定值,a的最大值为多少?
(3)a为定值,b的最小值为多少?
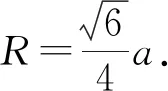
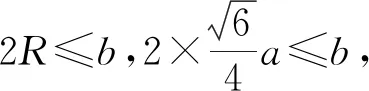
题型2.两个小正四面体在一个正方体内自由旋转
两个棱长为a的小正四面体A—BCD在棱长为b正方体EFGH—E1F1G1H1内自由旋转.
(1)a与b之间的不等关系是什么?
(2)b为定值,a的最大值为多少?
(3)a为定值,b的最小值为多少?
【解析】两个小正四面体的外接球放入正方体EFGH—E1F1G1H1的内切球内,则4R≤b.

3.一个正方体在一个正四面体内自由旋转
题型1.一个棱长为a的正方体ABCD—A1B1C1D1在一个棱长为b的正四面体E—FGH内自由旋转
(1)a与b之间的不等关系是什么?
(2)b为定值,a的最大值为多少?
(3)a为定值,b的最小值为多少?
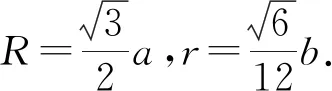

题型2.两个小正方体在一个大正四面体内自由旋转
两个棱长为a的小正方体ABCD—A1B1C1D1在一个棱长为b的大正四面体E—FGH内自由旋转.
(1)a与b之间的不等关系是什么?
(2)b为定值,a的最大值为多少?
(3)a为定值,b的最小值为多少?
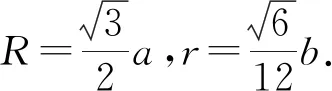
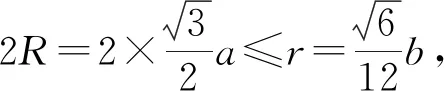
4.一个正方体在另一个正方体内自由旋转
题型1.一个棱长为a的正方体ABCD—A1B1C1D1在另一个棱长为b的正方体EFGH—E1F1G1H1内自由旋转
(1)a与b之间的不等关系是什么?
(2)b为定值,a的最大值为多少?
(3)a为定值,b的最小值为多少?
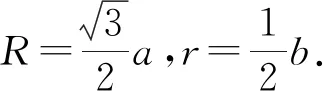
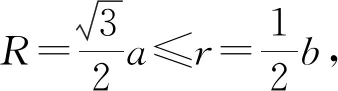
以上正四面体或正方体放入正四面体或正方体内自由旋转的基础思考,渗透了多面体的内切球与外接球的数量关系思考,为空间图形综合问题求解奠定了思维基石.
二、“自由旋转”测试题型
新高考数学在空间想象能力核心素养评价中,常将多面体与旋转体综合在一个问题中,最常见的题型是在题干中直接提供多面体与旋转体,然而“自由旋转”题型将旋转体隐藏在多面体中,提升了空间想象能力评价的力度,在一个问题中综合了两个多面体与两个旋转体(内切球与外接球),而且将它们的位置关系隐藏其中,这正是符合《普通高考数学课程标准》的水平测试的要求:“能够在熟悉的数学情境中,借助图形的性质和变换(平移、对称、旋转)发现数学规律;能够描述简单图形的位置关系和度量关系及其特有性质”.
测试题1(多选题)(浙江新阵地教育联盟2024届高三联考)已知正方体ABCD—A1B1C1D1的棱长为4,正四面体E—FGH的棱长为a,则以下说法正确的是
( )
A.正方体ABCD—A1B1C1D1的内切球直径为4
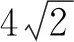

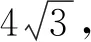
测试题2(多选题)已知正四面体A—BCD的棱长为4,正四面体E—FGH的棱长为a,则以下说法正确的是
( )


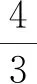
D.若正四面体A—BCD放入正四面体E—FGH内可以自由旋转,则a的最小值是3
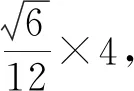
三、空间图形新题型拓展
空间图形的新题型着力于提升检测学生的空间想象能力,面对空间图形的新信息时,学生的理解是有层次的,于是,在高考立体几何复习训练中,要多种方式提升学生的空间想象能力.
几何模型训练法:利用立体几何中多面体(正方体,四面体等)模型,在直观教具引导下,养育学生的空间想象能力,比如,一个正方体模型,如图2,其中六个面的面对角线是用橡皮筋连接的.
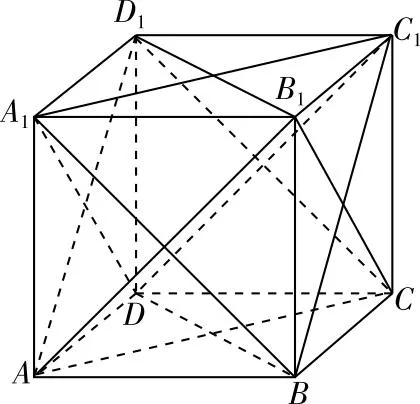
图2
请你构造一个面数大于6的多面体?画出设计的多面体的直观图.
变式1.正方体框的棱为铁丝,面对角线为橡皮筋,将一组对面的面对角线橡皮筋交点处向外拉,如果构成一个多面体,它是几面体?
变式2.正方体框的棱为铁丝,面对角线为橡皮筋,将两组对面的面对角线橡皮筋交点处向外拉,如果构成一个凸多面体,它是几面体?
变式3.正方体框的棱为铁丝,面对角线为橡皮筋,将三组对面的面对角线橡皮筋交点处向外拉,如果构成一个凸多面体,它是几面体?
变式4.变式1—3中,数一数它们有多少棱、多少个面、多少个顶点?棱数、面数、顶点数之间有什么规律吗?
列表来加以研究:
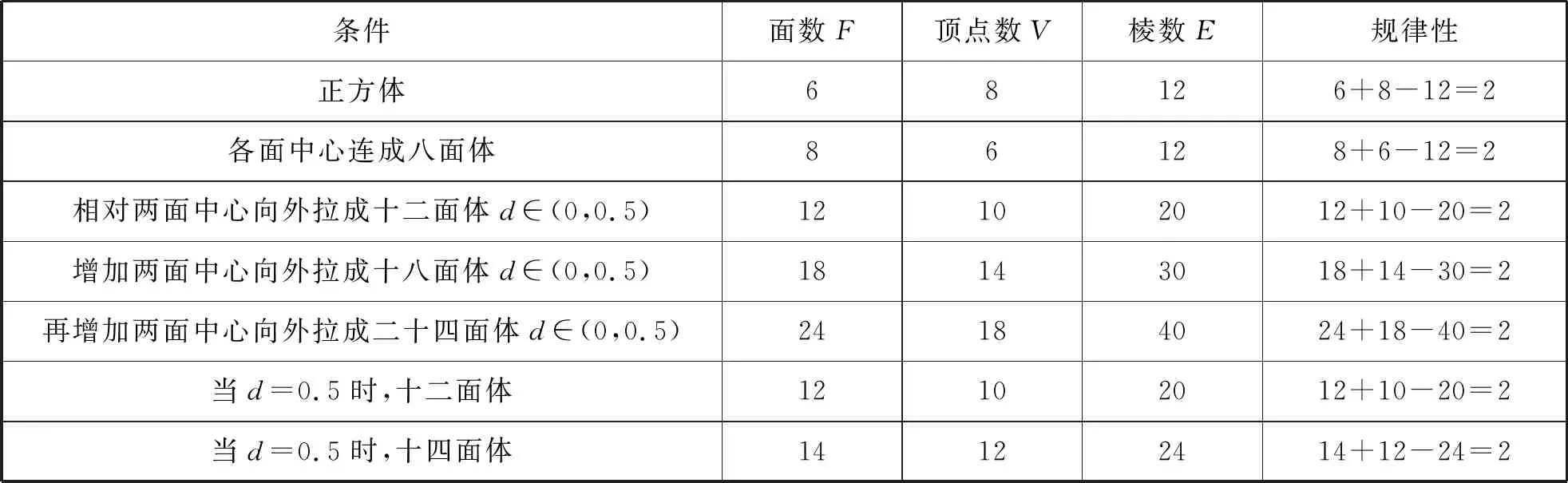
条件面数F顶点数V棱数E规律性正方体68126+8-12=2各面中心连成八面体86128+6-12=2相对两面中心向外拉成十二面体d∈(0,0.5)12102012+10-20=2增加两面中心向外拉成十八面体d∈(0,0.5)18143018+14-30=2再增加两面中心向外拉成二十四面体d∈(0,0.5)24184024+18-40=2当d=0.5时,十二面体12102012+10-20=2当d=0.5时,十四面体14122414+12-24=2
欧拉公式:F+V-E=2
逻辑推理训练法:立体几何中位置关系的推理证明是检测学生空间想象能力的重要阵地,比如,如图3,AC为圆O的直径,B为圆周上不与点A,C重合的点,PA垂直于圆O所在的平面,连接PB、PC、AB、BC,AN⊥PB,AS⊥PC,连接SN,试判断互相垂直的平面有哪几对?并能逆推法展示.

图3
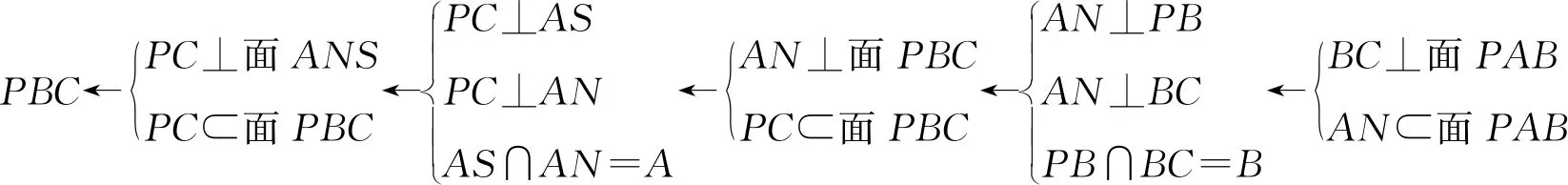
新高考数学试卷中的空间图形命题正在以检测学生“创新意识与实践能力”为目标,创设新颖题型(举例题、数据题、开放题等)来检测学生空间想象能力与逻辑推理能力,高三最后阶段数学复习,除了动手刷题训练外,动手举例实践与动脑提出问题的训练也十分必要,这样在高考数学考试中才能无实物空间想象与逻辑推理,才能培养或筛选出来创新型人才,以适应人工智能时代对人才的要求.

