一道关于内切球题目的多种解法
刘昌领
(湖北省通山县第一中学)
立体几何的内切球是立体几何模块重要内容之一,也是高考的热点问题之一,这类试题蕴含极为丰富的重要数学思想方法,对知识、方法、技能考查十分丰富,对逻辑推理、空间想象、数学建模、数学运算等核心素养考察全面,有很好的探究价值.笔者从一道关于内切球的题目切入,通过多维度多视角分析,得到三种解法.
一、原题呈现

本题以四棱锥为载体,在立体补形、等面积法、等体积法、解三角形等基础知识的交会处精心设计,能较好地甄别学生的逻辑思维水平和推理能力,是一道优秀的阶段性测试题.
二、解法探究
【分析1】由于所给条件是各侧面顶角相等,结合常见空间立体几何模型的结构特征,从而将其补形为正四棱锥.
【解法1】依题意可知:将四棱锥P-ABCD补成正四棱锥P-A1B1C1D1,如图1所示,易知所有棱长都相等,且PA⊥PC,PB⊥PD.

图1
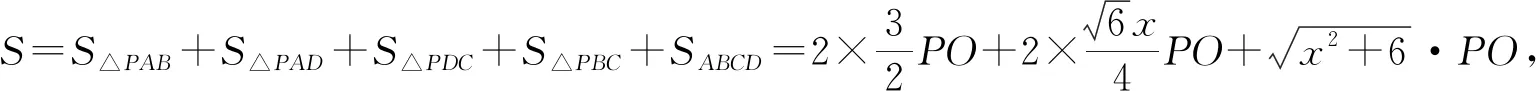
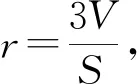
【分析2】由于补形为正四棱锥,而正四棱锥内心在高上,根据条件可分析出本题四棱锥内心也在高上,再利用正四棱锥边角关系可以方便计算出内心到顶点P的距离.
【解法2】如图2所示,设四棱锥P-ABCD内切球球心为Q,则Q到底面ABCD距离为1,如图3所示.
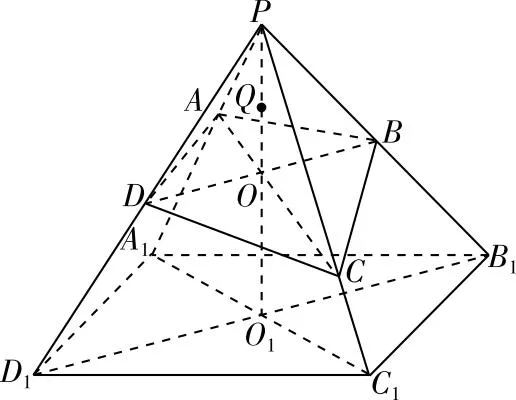
图2
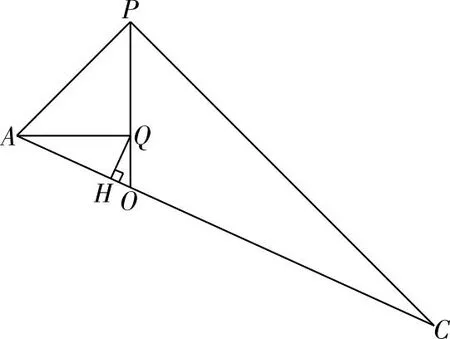
图3

【评注】结合内心和勾股定理逆定理,以及等面积法进行计算.本法比法一简单.
【分析3】根据正四棱锥底面中心与四棱锥底面中心和顶点三点共线,在△C1CT中,利用∠C1CT=∠PC1A-∠C1AH,和两角差的正弦公式解三角形.

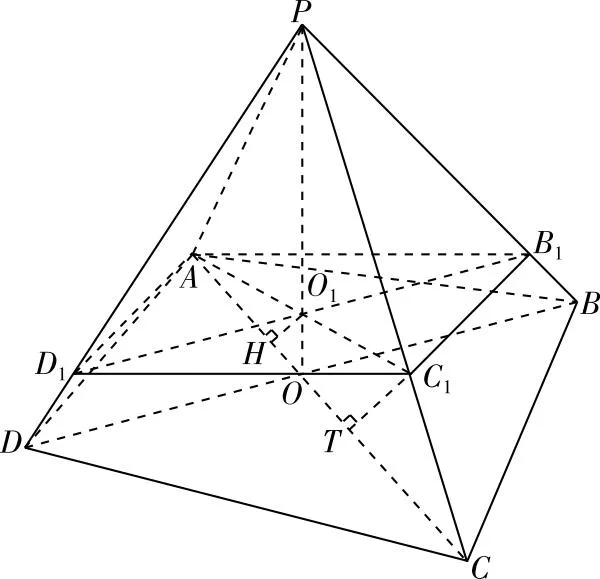
图4
∵PB=PD,PB1=PD1,∴BD∥B1D1.又∵B1D1⊥面PAC1,∴BD⊥面PAC1.又∵BD⊂面ABCD,∴面ABCD⊥面PAC.过O1作O1H⊥AC于H,则O1H⊥面ABCD,即O1H=1.过C1作C1T⊥AC于T,如图5所示.
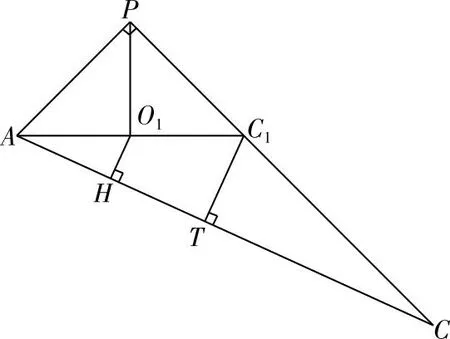
图5

三、一点感悟
本题得分率极低,分析原因有以下几种:一是学生不会补形,对于一个不规则的立体图形,第一感觉是恐慌,不敢尝试.二是很多学生盲目刷题,追求数量.感悟太少,对典型热点问题缺乏本质探索和深层次的研究,缺乏必要的拓展与延伸,不注重分析与思考;三是很多学生空间想象、逻辑推理、运算能力偏弱,一旦式子较复杂,就错误百出;四是很多学生面对压轴题直接放弃,信心严重不足.
数学知识内部逻辑联系紧密,很多问题可以多视角、多维度探索,寻求解决问题的最佳途径,一题多解一题多悟,提升自己发散思维的能力,揭示题目内部规律,使思维向更深层次发展.
在平时教学中,要注重引导学生从不同角度审视题目,从不同的知识点切入题目,寻求多维度、多视角、多层次的探究与思考,从而探究出不同的解决方案,对不同的解题方法进行纵横深入比较,拓宽解题思路,沟通不同知识,掌握解题规律,权衡不同解法的优劣,提高解题效率,提高分析问题和解决问题的能力.

