玉经雕琢方成器 剑拔沉埋便倚天
——记一道市质量检查试题的命制过程与感悟
陈崇荣
(福建省宁德市柘荣县第一中学)
璞玉经过雕琢终会成为精美的玉器,宝剑经过沉埋锻造才可以削铁断金.命制试题也是一样,只有投入大量的精力,经过不断的加工、打磨才能命制出一道好题,从而发挥对教学的导向作用.笔者有幸参加了2023年宁德市高三5月份质量检查试卷的命制,本文分享命制试卷中圆锥曲线试题的命制过程及感悟.
1.命题的依据及方向
首先认真研读《普通高中数学课程标准(2017年版)》和《中国高考评价体系》,《普通高中数学课程标准》在命题原则中着重强调对学生数学学科核心素养的考查.《中国高考评价体系》确立了“一核”“四层”“四翼”的整体框架,是高考命题的理论基础,提出命卷要体现基础性、综合性、应用性和创新性.结合近几年高考圆锥曲线试题的特点,制定命题方向及要求如下:
①试题的考查内容聚焦对重要数学概念、定理、方法、思想的理解和应用,注重数学本质、通性通法,淡化解题技巧.
②试题必须引导教学,对平时的教学起引导作用.因此坚持“源”于课本,高于课本的原则,兼顾试题的公平性,试题难度有梯度性,让大部分学生能入手,体现基础性,也有综合性,创新性.
③试题的考查体现核心素养的掌握.圆锥曲线是落实直观想象、数学运算,逻辑推理等核心素养的重要载体,因此要能较好地考查考生的数学运算能力,逻辑推理能力,直观想象能力,让学生掌握研究解析几何的基本方法—代数法,突出几何条件的代数转化能力,真正体会解析几何的本质.
2.立意与选材


图1
本题是课本例题,所求的轨迹是椭圆.可以对本题进行推广,得出以下结论:
结论1:设A,B两点的坐标分别为(-a,0),(a,0)(a>0).直线AM,BM相交于点M,且他们的斜率之积是m(m≠0),求点M的轨迹方程.(m<0,轨迹是椭圆;m>0,轨迹是双曲线)
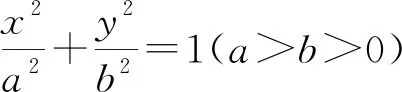
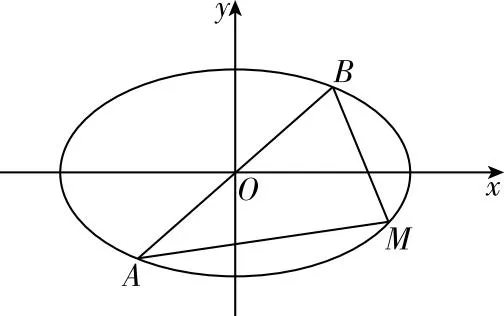
图2
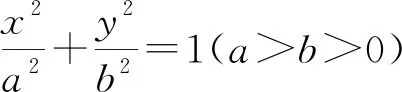

图3

图4

图5
【点评】波利亚曾说过:“观察可能导致发现,观察将揭示某种规则、模式或定律.”
通过课本例题,可以得出结论1、结论2、结论3,据此可以进行编制一些试题,而且符合源于教材,高于教材的命题原则.

(1)求C的方程:
(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明:存在定点Q,使得|DQ|为定值.
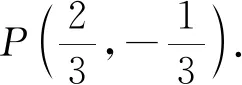

(1)求C的方程;

【点评】本题线段长度的合理代数化转化是解题的关键,用代数法研究几何问题是解析几何的本质,数形结合是解析几何的重要思想.该题通过探究可以得:若点T(x0,y0)是椭圆内任意一定点,过T的两条直线分别交椭圆C于A、B两点和P、Q两点,且满足TA·TB=TP·TQ,则直线kAB+kPQ=0,即A、B、P、Q四点共圆.
3.命题的命制与加工
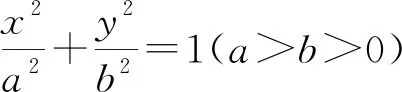
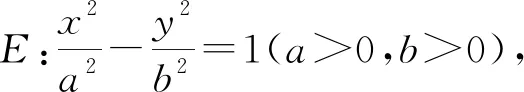
(1)求曲线E的方程;
(2)记E上不同的三点A,B,C,其中A为E的右顶点,若直线AB,AC的斜率之积为1,证明:直线BC过定点.
笔者正好参加高二的期末区域性学业质量检测命卷,圆锥曲线的解答题就定了这道题.但该题作为高三的5月份质量检测过于简单,需进行修改,于是再次改编如下:



2稿,3稿,4稿虽然难度比1稿提升了许多,先考查了直线AB过定点问题,接着利用平面几何性质求定值|DN|或者Q的轨迹方程,但是和2020年山东卷第22题太相似了,建议椭圆改为双曲线,同时结合题源3,与四点共圆的知识相交汇,于是就有了下面的第5稿.
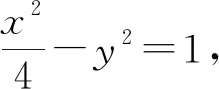
(1)求点D的轨迹方程.
(2)AD的延长线交曲线E于点Q,若∠ACB=∠BQA,求弦长BC.
试题第5稿出来后,命题组老师进行了讨论,凝聚共识,得出了以下几点修改意见:
①第一问偏难,达不到区分目的,而且作为高三5月份质量检测,应给学生多一些信心,建议第一问降低难度,给不同层次的考生水平得到合理评价.
②条件∠ACB=∠BQA不容易转化为四点共圆,建议条件更加直接一点.
③因为双曲线有左右两支,为了避免麻烦,限制点A、B、C在同一支.
④题目不够简洁,历届高考试题,第一问的已知条件相对简洁.
⑤求直线BC的斜率比求弦长BC更简洁.

(1)求E的方程;

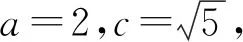

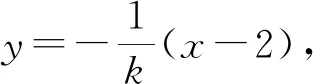
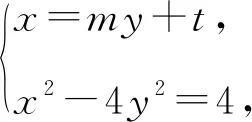
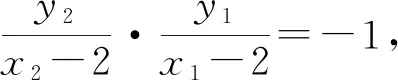
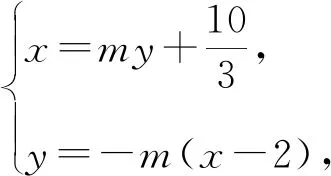
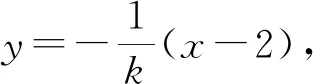
消去y得(1-4k2)x2+16k2x-16k2-4=0,
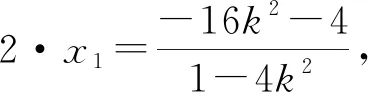
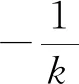
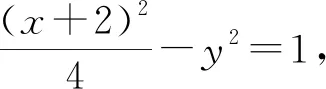

【点评】试题分步设问,逐步推进,具有区分度,注重对基本概念、基本方法的考查,考查内容由浅入深,层次分明,重点突出,源于课本又高于课本,能很好地引导中学数学教学回归课本.试题对考生的逻辑推理、直观想象、数学运算等数学核心素养,以及灵活地运用解析几何的基本方法将问题合理转化的能力有一定的要求,体现了用代数方法研究解析几何的本质,同时又体现了解析几何的几何本真.六种解法对比可以发现,解法一、二、三是通性通法,对运算素养有较高要求,体现解析几何的本质,能很好考查学生对解析几何基本方法的掌握程度.解法四、五、六计算量小,但较灵活,要求也较高,曲线系方程求解的方法,坐标平移的方法估计一部分学生不熟悉,但也有些学生通过网课、数学竞赛频繁有接触过.因此解法一、二、三列在前面,也是本题主推的参考答案.
4.命题感悟
华罗庚曾说,命题比解题难,命题要测得出水平,测得出能力.这就要求命题之前要认真研读《普通高中数学课程标准》、《中国高考评价体系》,熟悉历年的高考真题,确保命制的试题不偏离方向.
课本是众多专家智慧的结晶,课本是发展学生核心素养的载体,课本的例题、习题是命题之源.平时教学中认真钻研教材,对课本例题、习题或者阅读材料等进行深入研究,对其进行变式、推广、迁移、整合.只有平时积累了素材,后期的试题命制才不会“无米之炊”.
选好素材后要精雕细琢,不断打磨,提出符合学生认知能力的问题,不宜出太难或者复杂的问题,命制的试题要具有良好的区分度,入口要宽,一题多解,让不同层次学生的水平得到合理的评价.

