齐次化构造妙解双斜率问题
张秀妮
(山东省威海市文登区教育教学研究中心)
圆锥曲线中的双斜率问题,一直是高考考查的热点题型.但学生得分率很低,究其原因,主要是选择方法不当,导致运算量极大,失去计算热情.本文通过齐次化构造的方法,帮助学生减少运算量,用平面几何的视角,探究圆锥曲线中轴点弦定理和等角定理.
一、齐次化构造背景介绍
1.齐次式
一个多项式中,如果各项的次数都相同,则称这个多项式为齐次式.
例如:x+y是一次齐次式,x2+3xy+y2是二次齐次式.
2.齐次方程
如果一个方程中,所有非零项的次数都相同,则称这个方程为齐次方程.
3.基本原理

二、斜率之和问题



【解法1】采用常规解法,难点在于题目涉及的直线相对较多,学生不知道应该设哪条直线.在通常情况下,求哪条直线的信息,我们就设这条直线的方程.
由题意知直线l斜率存在,设为k,则直线l:y=kx+m,

可得,(1-2k2)x2-4kmx-2m2-2=0.
设P(x1,y1),Q(x2,y2),
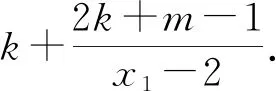
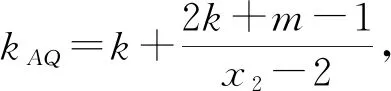
因为kAP+kAQ=0,所以k=-1.
【解法2】采用齐次化构造方法,已知kAP+kAQ的值,联想到韦达定理中的两根之和,所以需要构造一个以kAP,kAQ为根的一元二次方程Ak2+Bk+C=0.


即A(y-1)2+B(y-1)(x-2)+C(x-2)2=0 (*),
而(*)是关于(x-2)与(y-1)的二次齐次式.因为斜率中的变量x,y来自双曲线,所以我们想将双曲线中的变量凑成(x-2)与(y-1)的形式:
(x-2)2+4(x-2)-2(y-1)2+4(y-1)=0
(**).
不难发现(**)中(x-2)与(y-1)并非齐次式,所以我们需要把(**)的一次项凑成二次项.如何实现?其实,斜率中的变量x,y不仅来自双曲线,还来自直线l.所以,我们首要的任务是将直线l的方程改写成(x-2)与(y-1)的形式.
【引理】给定直线l和直线外一点P(x0,y0),则直线l的方程可以写为m(x-x0)+n(y-y0)=1.
证明:直线l可写为Ax+By+C=0,其中A2+B2≠0.
因为A(x-x0)+B(y-y0)=-(Ax0+By0+C),
P(x0,y0)∉l,所以Ax0+By0+C≠0.

所以直线l可设为:m(x-2)+n(y-1)=1,
所以(x-2)2+4(x-2)[m(x-2)+n(y-1)]-2(y-1)2+4(y-1)[m(x-2)+n(y-1)]=0,
整理可得(4n-2)(y-1)2+(4n+4m)(y-1)(x-2)+(1+4m)(x-2)2=0,
即(4n-2)k2+(4n+4m)k+(1+4m)=0,

所以n=-m,即k=-1.
对比两种解法,不难发现,在处理双斜率的和或积的相关问题中,齐次化构造更为便捷.
三、斜率之积问题
以圆锥曲线的轴点弦定理为例:
【轴点弦定理】过圆锥曲线(椭圆、双曲线、抛物线)对称轴上非顶点的一定点的直线与圆锥曲线交于不同的两点,则这两点与相应对称轴上的一个顶点所连斜率之积为定值.
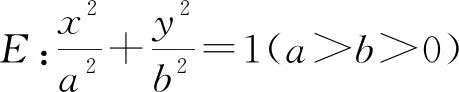

下面运用齐次化构造对此定理进行简单证明.
【解析】设直线AB:m(x+a)+ny=1,

整理可得b2(x+a)2-2ab2(x+a)+a2y2=0,
所以b2(x+a)2-2ab2(x+a)[m(x+a)+ny]+a2y2=0,
整理可得a2k2-2ab2k+b2-2ab2m=0.



【抛物线轴点弦定理】过定点P(t,0),t≠0的直线l与抛物线E:y2=2px(p>0)交于A,B两点,则kOA·kOB为定值.特别地,当P(2p,0)时,OA⊥OB.
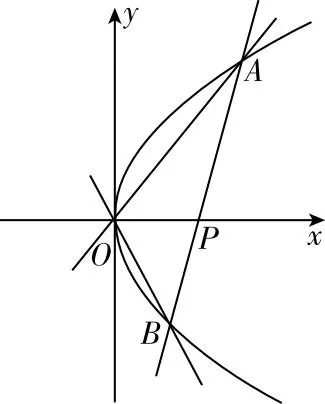
大家可以尝试用齐次化构造的方法证明上述两个定理.
【反思】轴点弦定理只是告诉我们如果直线AB过定点,则相应轴的一个顶点与A,B所连直线的斜率之积为定值;反之,结论未必成立,但绝大多数情况下是成立的.因此我们可以运用这个结论进行大胆地猜测,然后用齐次化构造仔细验证.下面借助一道统考试题,看一下.

(1)求证:BM⊥BN;
(2)设直线BM交椭圆C于另一点Q,求证:直线PQ恒过定点.
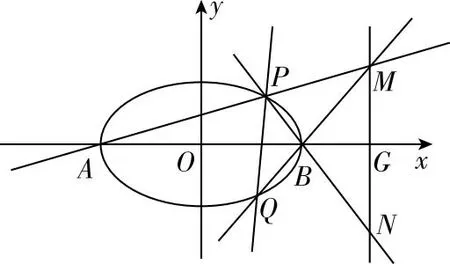
【解析】(1)证明略.
证明:设直线PQ方程为m(x-2)+ny=1,
整理可得(x-2)2+4(x-2)+4y2=0,
所以(x-2)2+4(x-2)[m(x-2)+ny]+4y2=0,
整理可得4k2+4nk+1+4m=0.


四、转化提升
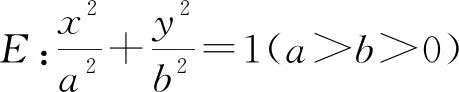



【抛物线等角定理】过抛物线E:y2=2px(p>0)对称轴上一定点P(t,0)(t≠0)的弦AB的两端点与对应点Q(-t,0)连线与对称轴(即x轴)所成的锐角相等.

我们以抛物线等角定理为例,运用齐次化构造的方法进行证明.
证明:所求问题可转化为求kQA+kQB=0.
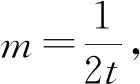
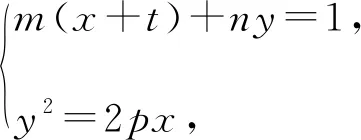
整理可得y2-2p(x+t)+2pt=0,
所以y2-2p(x+t)[m(x+t)+ny]+2pt[m(x+t)+ny]2=0,
整理可得(2ptn2+1)k2+(4ptmn-2pn)k+2ptm2-2pm=0,
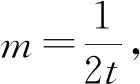
大家可以尝试用齐次化构造的方法证明上述椭圆和双曲线的等角定理.
【思维拓展】椭圆与双曲线有两条对称轴,所以只要M、N成对地出现在同一条对称轴上,命题依然成立,即:
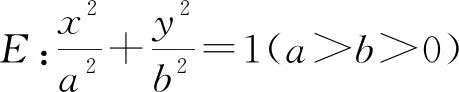


(1)当l⊥x轴时,求直线AM方程;
(2)O为坐标原点,证明:∠OMA=∠OMB.
【解析】(1)解答略;

(2)证明:设直线l方程为m(x-2)+ny=1,
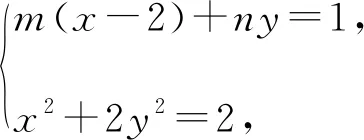
整理可得(x-2)2+4(x-2)+2y2+2=0,
所以(x-2)2+4(x-2)[m(x-2)+ny]+2y2+2[m(x-2)+ny]2=0,
整理可得(2n2+2)k2+(4n+4mn)k+1+4m+2m2=0,
因为F∈l,所以m=-1,
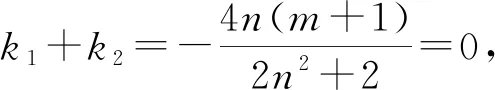
所以∠OMA=∠OMB.
【反思】齐次化构造法比常规做法,运算量大大降低.但本方法,适用于斜率的相关问题,有很大的局限性.更大的难点是如何通过审题,将所求问题转化为斜率之积与和的问题.

