数形结合探思路,深度分析练思维
张建文
(甘肃省岷县第一中学)
直观想象素养是高中数学六大核心素养之一,是数学思维能力的重要体现.培养直观想象素养的主要方式就是在不断解决问题的过程中逐步训练学生的运用数形结合思想的能力.图象是函数的直观表示,更是函数的灵魂,函数问题的分析解答通常是以其图象为引路方向,函数图象通常引导文本书写过程,函数图象的展现使得函数富有生机与趣味.
深度分析与浅显表达是培养学生思维的重要方式.所谓深度分析就是在原问题解决的基础上探究其发生的深层次原因以及更一般化的结论,而浅显表达则是在深度分析的基础上用比较浅显而直观的语言解释与表达.在函数图象教学过程中,深度分析主要从“一点两线”进行探究,引导学生体会绘制函数图象过程中的严谨性和准确性.
1.探究函数的“关键点”——分界点.函数有零点、驻点、极值点和拐点等,不同类型的点处于函数图象的不同位置.一般地,零点区分函数值的正负,是函数图象处于x轴上下部分的分界点;极值点是函数单调性变化的分界点,而拐点是函数增减速率变化的分界点.
2.探究端点附近的“亲密线”——渐近线.若函数f(x)定义在区间(x0,+∞),且f(x0)无意义,则f(x)可能存在渐近线.通过定量分析而实现定性判断,进而绘制准确的函数图象.渐近线的意义在于确定函数图象的边界,能够直观确定函数的属性,蕴含着极限思想和几何美感.
3.探究函数的“放缩线”——切割线.切线是割线的极限位置,切线与割线相伴而生,借助切割线能够对函数值进行有效放缩,在不等式证明和函数值近似计算过程中发挥着不可代替的价值,同时通过图象观察利用切割线进行数值放缩是比较直观而易得的思路.
数形结合是一种问题解决方法,更是培养学生直观想象素养的有效手段.在函数问题中,数与形的结合通常体现为函数解析式与函数图象的有机结合与转化,具体包括“由式探形”与“以形助式”这两个方面.利用数形结合思想解决问题,最终都是先以式探形,再以形助式,其基本流程是:式→形→式.本文重点以例说明如何利用数形结合思想进行深度分析.
一、由式探形
由式探形就是根据函数解析式或等价函数绘制函数图象并探究函数图象的“一点两线”,通常借助方程f(x)=0,f′(x)=0和[f′(x)]′来探究“关键点”,利用导数值的正负确定函数单调性,利用洛必达法则求极限来探究函数图象的渐近线.
1.求极限探渐近线,求二阶导找拐点
渐近线是函数图象的辅助直线,是函数图象在某一区域内无限靠近但无法相交的直线,对于理解函数单调性和值域有重要意义.一般地,通过探究函数值的变化情况来研究渐近线.在函数单调性明确的情况下,我们通常会进一步探究函数图象的凹凸性,以期达到深度分析和强化训练思维的效果.
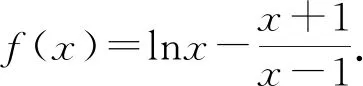


图1
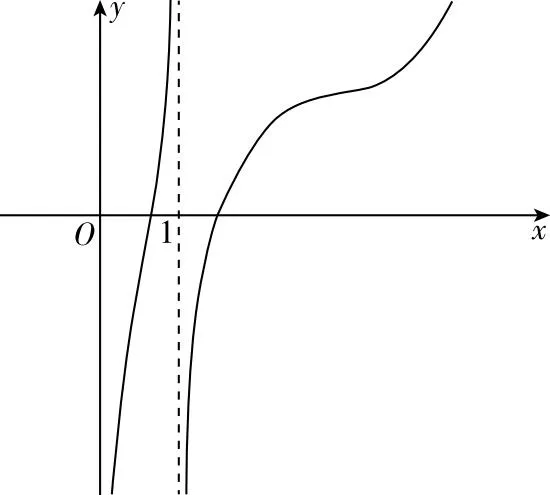
图2

小结与反思:函数单调性的判断不仅要观察导函数的正负,更要看定义域的组成形式,若定义域是中间断开的,函数有可能存在渐近线,需要我们利用洛必达法则进行深入判断.同时利用二阶导数可以进一步判断单调函数增减速率变化情况,由式探形,进一步准确绘制函数图象.
2.看式似有渐近线,洛必达法则解惑
根据以往经验,分式函数在分母为零的位置通常会存在渐近线,但在某些特殊函数中并不存在渐近线,就需要我们利用洛必达法则求极限来判断.


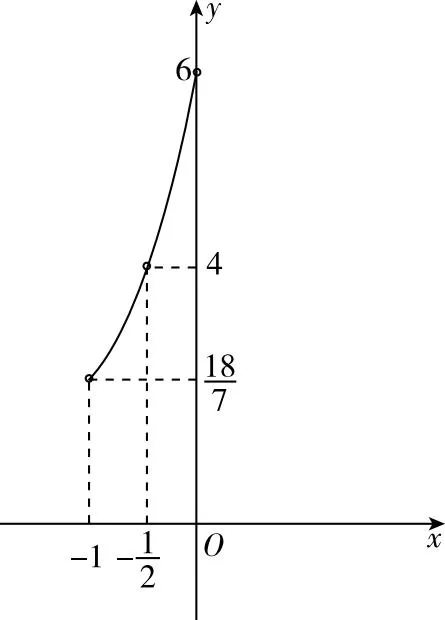
图3

3.观式构图辨位置,导数正负巧判断
导数正负判断是确定函数单调性的前提,对于复杂导数结构中的部分因式,在保证其正负取值一致的情况下,我们通常将其等价转化成较简单的式子,再通过构造函数画简图来确定导数的正负.
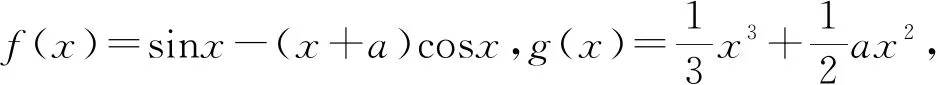
(1)讨论函数f(x)在(0,π)上的单调性;
(2)若h(x)=f(x)-g(x),判断h(x)的单调性.
深度分析:(1)f(x)=sinx-(x+a)cosx,则f′(x)=(x+a)sinx,x∈(0,π).可知sinx>0,f′(x)的正负由x+a决定.令x+a=0,得x=-a,-a与(0,π)的关系有三种情况,所以y=x+a的图象与(0,π)的关系也有三种情况,如图4.

图4
①当-a≤0,即a≥0时,有x+a>0,f′(x)>0,所以f(x)在(0,π)上单调递增;
②当-a≥π,即a≤-π时,有x+a<0,f′(x)<0,所以f(x)在(0,π)上单调递减;
③当0<-a<π,即-π


图5
①当-a>0,即a<0时,m(x)的单调递增区间为(0,-a),递减区间为(-∞,0)和(-a,+∞);②当-a<0,即a>0时,m(x)的单调递增区间为(-a,0),递减区间为(-∞,-a)和(0,+∞);③当-a=0,即a=0时,m(x)在R上单调递减.
小结与反思:利用导数判断函数单调性关键在于确定导函数的正负取值,通过将导函数进行等价转化成比较简单的函数,再根据其函数图象来判断函数值的正负,从而确定原函数的单调性,需要注意的是,根据转化后的函数图象不能判断原函数增减的快慢.在具体教学过程中我们可以比较转化与不转化之间的异同,体会转化后函数图象的神奇功效.
二.以形助式
以形助式就是借助函数图象或是等价图形,从中获得问题解答思路或是对原问题进行等价变形.一般地,在函数问题解决过程中,函数图象作为函数问题解答的灵魂,起着隐形统领作用.
1.绘制切线与割线,放缩证明不等式
切线是割线的极限形式,切割线是与函数图象联系紧密的两种直线.一般地,放缩有两个方向:①纵向放缩,就是借助切线将函数值在切点附近进行放大或缩小,或是求解函数值的近似值;②横向放缩,就是将函数图象上的点左移或右移到切割线上,从而实现对图象上点的横坐标进行放缩.切割线放缩法是一种证明不等式的重要手段,需要借助函数图象的凹凸性,对函数图象的绘制要求较高,在证明过程中能达到事半功倍的效果.

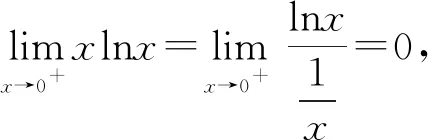

图6
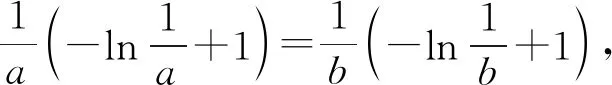

图7
所以x1+x2 小结与反思:切割线放缩法是证明不等式的一种重要方法,就是结合函数图象的凹凸性,利用切线和割线对自变量或函数值进行放大或缩小,通常进行一次放缩或两次放缩.本题经过两次放缩,恰好证明了结论成立.在实际教学过程中,引导学生探究图象的结构特点,挖掘图象中隐含的信息,体会数形结合的数学思想. 公切线的证明通常有两种方法:方法一,先求出曲线1的切线方程,再求出曲线2的切线方程,最后说明这两条切线为同一条直线;方法二,先分别找出曲线1和曲线2的切点A,B,再分别计算曲线1和曲线2在切点处的切线斜率k1,k2和直线AB的斜率kAB,最后验证k1=k2=kAB.在具体问题中,应坚持具体问题具体分析,尝试选择最优解答方法. 图8 图9 在恒成立问题解答中,若分离参数等方法难以实现,而且在端点处恰好满足条件,则可以先找不等式成立的必要条件,再证明其充分性即可.在整个分析过程中,不等式作为明线,函数图象作为暗线来引导问题解决. 小结与反思:在此问题解答过程中恰好有g(1)=0,而且分离参数等其他方法处理比较困难,所以我们可以考虑寻找其必要条件.结合函数简图(图10),存在δ使得g(x)在(1,δ)内递增,即有g′(1)≥0,进而得到一个必要条件,再证明其充分性即可.在实际教学过程中,要引导学生自然而然地思考问题,体会数学计算与证明的严谨性. 图10 在直观想象素养的培养目标上,课标要求能够通过想象对复杂的数学问题进行直观表达,反映数学问题的本质,形成解决问题的思路,能够在综合的情境中,借助图形,通过直观想象提出数学问题.在具体教学过程中,教师要设置恰当问题情境,从“由式探形”和“以形助式”这两个方面引导学生进行思考.对于数学问题的分析解答我们不能满足于具体问题的答案,需要探究更一般的问题解答模型,引导学生深度分析准确理解.2.以斜率寻找切点,两线合一证结论
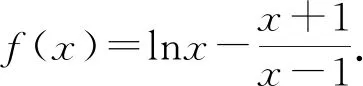
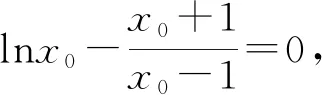



3.起始点引领探路,充要性严谨证明





三、总结与展望

