一道2023年模考题的多视角探究

广东省云浮市黄岗实验中学 (527400) 陈汉邦

一、问题呈现与解法探究

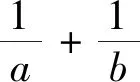
本题是二元约束条件下的二元函数最值问题,试题简洁、对称、优美,有一定的难度,本文给出多种视角下的解法.

视角1 拆项+均值不等式

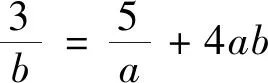
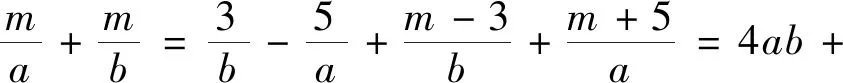
视角2 升幂+比值换元+均值不等式

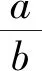
视角3 函数视角

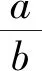
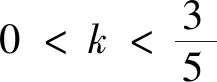
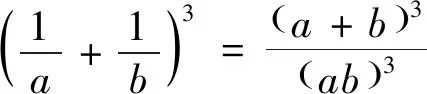
视角4 用求根公式减元

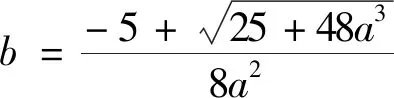
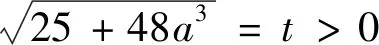
视角5 双换元+均值不等式

二、变式拓展

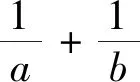
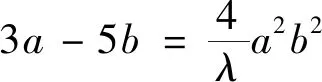
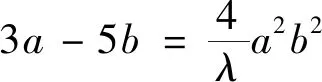
三、试题背景

本题背景是拉格朗日乘数法求极值问题,拉格朗日乘数法时高等数学中求多元函数条件极值的重要方法,方法程序性强,容易掌握,其优点,一是把目标函数和等式约束统一到一个拉格朗日函数中;二是把条件最值问题转化为无条件最值问题.对文首模考试题,应用拉格朗日乘数法解答如下.

四、追本溯源

本题是一道对思维有较高要求的好题,试题与教材有着紧密的联系,体现了高考命题源于教材、高于教材的理念.本题来源于人教2019版(数学)选修1第58页综合运用第5题:若a>0,b>0,且ab=a+b+3,求ab的取值范围.这题课本习题就是采用化二元为一元的策略去处理,与本题相通.因此,教师在教学中应重视对课本习题的深度挖掘,挖掘其中蕴含的数学背景、剖析背后的数学本质,感悟试题设计所蕴含的数学思想等.