一道教材习题在求解高考题中的应用

广东省珠海市广东实验中学金湾学校 (519040) 汪 文

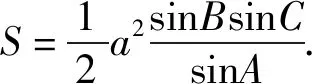
例1 (2023新课标全国卷Ⅰ)已知ΔABC中,A+B=3C,2sin(A-C)=sinB.

(1)求sinA;(2)设AB=5,求AB边上的高.

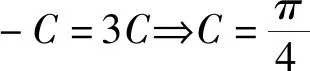
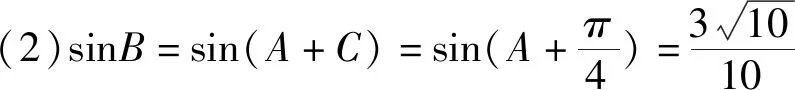
评注:由第(1)问的结果可轻松求得各角的正弦值,借助其中一边长得到面积,进而求得边上的高线长.

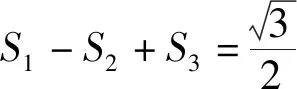
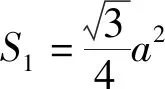
评注:借助面积公式和第(1)问的结果,第(2)问可以轻松得到,提高了效率.

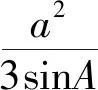
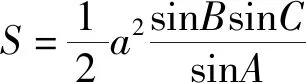
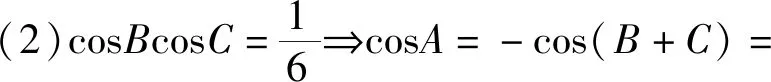
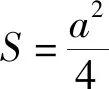
解析:(1)由正弦定理得b+c=2acosB⟹sinB+sinC=2sinAcosB⟹sinB+sin(A+B)=2sinAcosB⟹sinB+sinAcosB+cosAsinB=2sinAcosB⟹sinB=sin(A-B)⟹B=A-B⟹A=2B,得证.

评注:第(1)问将边换成正弦合并后即可得证,第(2)借助面积公式二倍角公式和诱导公式求得∠A大小.

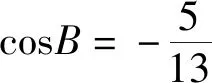
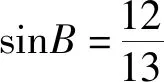
评注:第(1)问利用两角和的正弦公式可得,第(2)借助面积公式可快速求出BC的长.

教材是学生学习的中心,根植于教材,来源于课本,着眼于提高是很多高考试题的真实写照,在高考复习中,让学生回归教材,重视课本的再学习,看清课本习题与高考题之间的联系,揭开高考试题的神秘面纱,既让学生看清了问题的本质,又让学生学会了思考,从而达到了事半功倍的复习效果.