2023年全国新高考Ⅰ卷解几压轴题解法探究*

江苏省苏州第一中学 (215000) 王 耀 蔡玉书

在2023年全国高考数学新高考Ⅰ卷中,压轴题是一道解析几何试题,命题者以直线和抛物线的位置关系为命题背景,巧妙地设计了矩形周长的最值问题,对学生的应用数学知识的能力进行了有效地考查.本文以此题为例,从不同的角度研究其解题思路,并总结一般性结论,与读者分享.

1.试题呈现

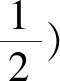
2.解法探究

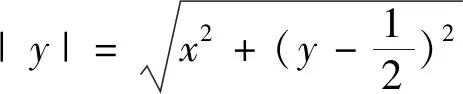
第(2)问,在处理解析几何问题时,常用的方法是设k法,直线与圆锥曲线进行联立方程组,利用斜率k表示弦长,再进行求解:

思路一引入双参数:点A的坐标,直线AB和AD的斜率.利用直线与抛物线方程进行“曲直”联立,得到弦长之和的表达式,通过分类讨论处理双绝对值函数的最小值问题.

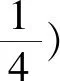
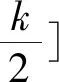
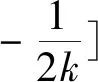
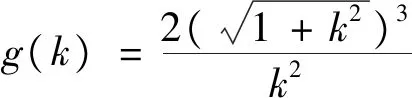
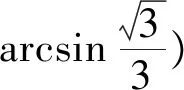
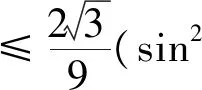
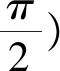
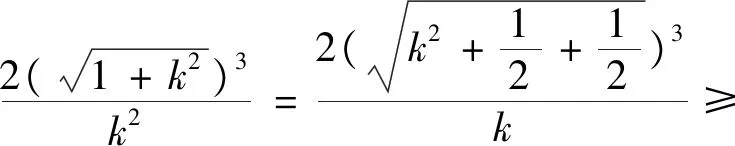
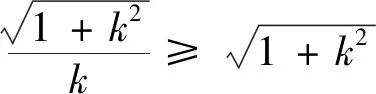
在国家考试中心网站上,还给出了利用直线的方向向量来处理旋转90°的几何问题,即如下的设角法:

思路二引入双参数:点、角度,即长方形的三个顶点的坐标,再引入相邻两边所在直线的方向向量、法向量,从而可表示矩形各边的长度,并得到证明.

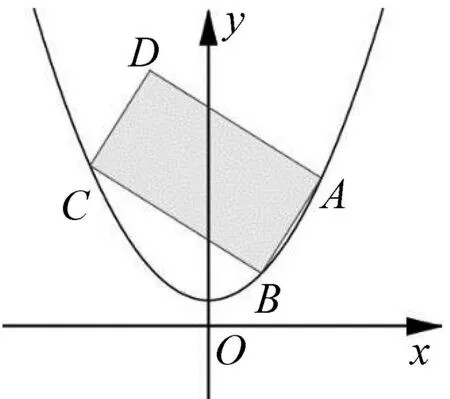
图1

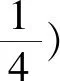
笔者研究后发现,人教A版(2019年)新教材非常重视向量在新知证明中的应用,上述思路中,在直线的方向向量、法向量的双重作用下,顺利得到长度和角度的等量关系. 事实上,笔者回顾平时的教学过程,在处理与旋转相关的几何问题时,既可以使用直线的参数方程的几何意义来求解,也可以使用圆的参数方程去运算,最终转化为三角函数的最值问题.即如下两种求解思路:

思路三引入双参数:点A的坐标,直线AB的倾斜角θ.利用直线参数方程的几何意义进行求解.

图2

证法3:由平移的不变性,将抛物线化为y=x2考虑(如图2).

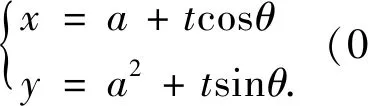
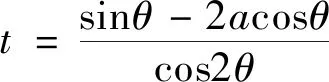
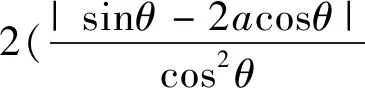
思路四引入双参数:点A的坐标,线段AB的长r1.利用圆的参数方程的表示r1,同理可表示AC的长r2.得到关系式进行分析.

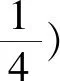
上述思考角度最终都转化为三角函数问题,事实上,若直接引入点的坐标进行运算(设点法),也能找出其中的等量关系后,再利用两点距离公式进行求证:

思路五引入三参数:点A,B,D的坐标.利用AB⊥AD找出参数之间的内在联系,进行转化求解.

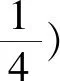
由AB⊥AC可知(a-b,a2-b2)·(a-d,a2-d2)=0,化简得(a+b) (a+d)=-1.

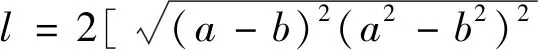
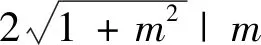
3.一般性结论及试题溯源

根据前面的几种解题思路,进一步研究后,还能得到如下一般化结论,并将问题进行题源追溯,可以发现与1998年的上海市高中数学联赛试题有相似性,一并整理如下:

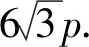
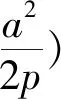
结论2 已知矩形ABCD有三个顶点在抛物线W:x2=2py(p>0)上,则矩形ABCD的对角线长的最小值为4p.

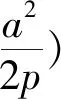
题源(1998年上海市高中数学竞赛)一个正方形的三个顶点A,B,C在抛物线y=x2上,求正方形面积的最小值.

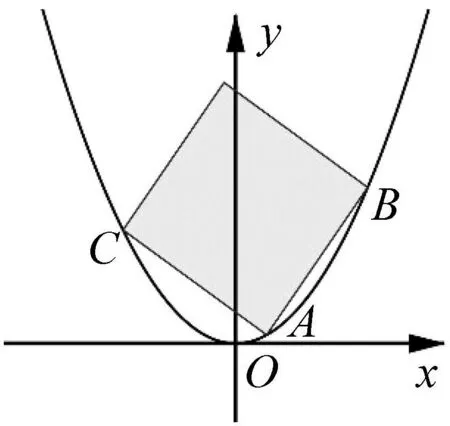
图3

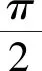
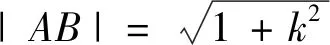
4.题后反思

美国数学家、心理学家哈尔莫斯曾经在《数学的心脏》一文中指出:“问题是数学的心脏”.的确如此, 问起于题,疑源于思,本文中,从一道高考压轴题的解法开展思考,自觉以问题为中心,不断地进行探寻通法,优化解法,解法之间有联系,更有创新,各具特色.由此可见,面对数学问题,只要学会广泛的联想和生动的类比,就会发现宽阔的思路,探究出各式各样的方法来. 如果在解题过程中,对于每一个细节再进一步深入思考,继续追寻下去,那么解法还能不断改进,不断优化,化复杂为简单,聚分散为统一.