平面向量模问题的求解策略研究*——从一道高考真题说起

福建省福安市第一中学 (355000) 徐志刚

平面向量是高考命题的重要考点,尤其是平面向量模的问题,时常出现在高考题的填空题中.我们知道,向量既有大小又有方向,这里的大小就是指向量的模,也叫向量的长度.计算向量的模或模的最值(取值范围)是一类常考题型.那么这类问题该如何破解,本文从一道高考真题谈起.

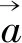
本题题干中的两个向量满足的条件都是以向量模的形式出现,无论是已知条件还是所求结论都统一到向量的模这个“焦点”上,主题十分明确.可以说,本题是一道语言精炼,考点明确不可多得的好题.那么这道题该如何解呢?

首先,我们都知道向量模的运算往往与两类的数量积有关,于是出现了一下两种思路:

思路1直接利用向量数量积的律运算求解

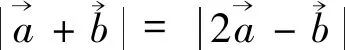
思路2换元再结合数量积的运算律求解

上述两种解法只是表述上的不同,实质是一致的,有时应用了向量的数量积运算的有关公式.其实,在求解向量问题时,还有一种方法不可忽视,那就是坐标法.

思路3引入向量坐标,转化为方程组

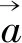
解答高考题,直接法固然是最常用的方法,但对于单选题与填空题来说,特殊化法有时省时又省力,值得尝试.

思路4应用特殊化思想

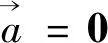
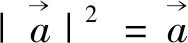
为了更好的研究这类问题,我们不妨将上述高考真题加以变式后再作研究.

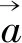
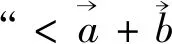
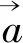
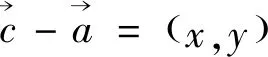
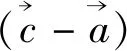
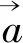
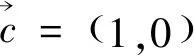
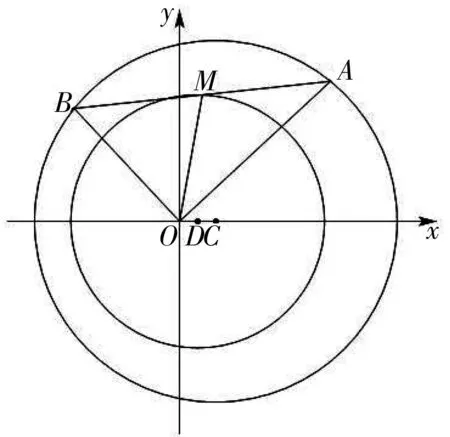
图1

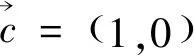
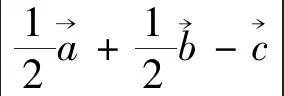
点评:本题考查向量模的取值范围的求解,对于较为复杂的题型,一般可以考虑将向量特殊化、坐标化来处理,利用解析法结合平面几何的相关知识、向量模的三角不等式来求解.