基于双液晶偏振光栅的机载光电跟瞄平台技术研究

张季丰，宋延嵩，王俊尧，刘洋

（长春理工大学 光电工程学院 光电测控与光信息传输技术教育部重点实验室，长春 130022）

0 引言

随着光电跟瞄技术的不断进步，光电跟瞄平台在机载平台中的应用日益广泛，而在某些特殊情况下由于安装空间狭窄、平台载重有限和更高要求的跟瞄精度与响应速度等因素使得传统光电跟瞄设备的应用受到极大限制［1-3］。液晶偏振光栅是一种衍射光学元件，它由平面单轴双折射液晶分子构成，液晶分子矢量随其位置呈周期性变化；不同偏振态的光束经过其衍射后出射光束不同于一般光栅，由于其偏振特性当线偏振光束经过其衍射后出射能量主要集中并均分于±1 级，经1/4 波片检偏后可保留单一光束用于目标跟瞄；当入射光束为左旋或右旋偏振光束时，出射光束主要集中于-1 级或+1 级，该特性为液晶偏振光栅光束偏转的基础。双液晶偏振光栅光电跟瞄设备是一种通过旋转两共轴液晶偏振光栅进行光束偏转的新型光束偏转设备，该设备具有转动惯量小、体积小、跟踪精度高等优点。在激光雷达、自由空间激光通信、激光制导、空间观测等领域，双液晶偏振光栅光束偏转机构因其结构紧凑、偏转角度大、指向精度高、动态特性好、可靠性高等优点，在激光光束扫描、瞄准和目标跟踪等方面具有广阔的应用前景［4-5］。

2009 年，KIM J 等［6-8］提出了“双液晶偏振光栅”的光束控制系统，该系统由正交圆偏振干涉内接的两个独立旋转的偏振光栅组成。通过两共轴旋转光栅控制衍射出射光束，可以在固定区域内进行轨迹扫描。实现双液晶偏振光栅或Risley 棱镜光束偏转的基础是光束偏转反向公式的推导及验证，2015 年，同济大学李安虎等［9］针对现有Risley 双棱镜反向解算公式解算精度较低的问题进行研究分析，对现有基于两步法反向解算公式进行改进，提出了利用正反向公式迭代的方法，使系统指向误差小于0.000 1 mm，并进行了轨迹扫描验证。2016 年， ZHOU Y 团队［10］使用两个独立旋转的偏振光栅实现了光束偏转指向，称之为Risley 光栅，其方式类似于Risley 棱镜，并对其正反向光束偏转解算公式进行了分析，并进行了轨迹扫描实验。2020 年，同济大学李安虎团队［11］利用光束矢量传播方法推导了从目标到相机的旋转Risley 双棱镜的迭代成像跟踪模型，实现了对运动速度为50 mm/s 移动目标的跟踪实验，跟踪误差低于8.5 像素的跟踪实验。该实验虽实现了双透射镜片系统光束跟瞄实验，但跟踪目标速度较慢并且其迭代法位置解算模型计算时间较长不能应用于载体扰动快速目标跟瞄场景中。液晶偏振光栅由于其独特的衍射特性，已成为新型光束偏转技术领域研究热点。而现阶段级联液晶偏振光栅系统的研究停留在光束大角度偏转指向等问题［12-14］，级联液晶偏振光栅系统光束偏转存在最小偏转角度导致其光束偏转不连续，与其相比通过两片液晶偏振光栅共轴旋转进行光束偏转可以实现偏折光束角度连续变化，角度变化分辨率为0.001°；与Risley 棱镜光电跟瞄系统相比，该系统利用液晶偏振光栅薄板对大体积、大质量的棱镜进行替代从而使双液晶偏振光栅光电跟瞄系统获得了更小的体积质量与转动惯量。综合上述研究分析，双棱镜光电设备多集中于光束指向扫描等领域，而液晶偏振光栅研究集中于理论模型推导、光束指向扫描与级联大角度偏转等领域。为将双透镜式光电跟瞄设备向机载激光通信等工程应用领域进一步拓展，将双液晶偏振光栅光束偏转模型与空间角度解耦算法相结合并制定详细跟瞄控制策略，再进行双轴载体扰动情况下的目标跟瞄实验，实现系统在模拟机载扰动情况下的稳定跟踪。

双液晶偏振光栅系统进行机载跟瞄的基础是明确其反向解算模型，并制定控制策略。本文研究以拓展液晶偏振光栅系统在机载激光通信、光电跟瞄等工程领域中的实际应用为目的，设计了一种基于视轴解耦与双液晶偏振光栅反向解算公式相结合的跟踪模型，并结合线性二次型调节器（Linear Quadratic Regulator，LQR）最优控制理论对这一新型光电跟瞄系统的跟踪性能进行实验测试，验证了跟踪模型的有效性。

1 双液晶偏振光栅跟踪原理分析

1.1 正向指向原理

在激光通信、光电跟踪等工程领域中，需要对探测器捕捉到的光斑进行实时跟踪对准。在目标跟踪理论和应用中旋转双液晶偏振光栅进行目标跟踪的基本前提是得到两片光栅的旋转角度与出射光束偏转角度之间的数学关系，其可分为正向解算过程和反向解算过程。通过两光栅的当前旋转角度推算出射光束的偏折角度为正向解算过程，通过出射光束的偏转角度推算出双液晶偏振光栅旋转角度为反向解算过程，双液晶偏振光栅跟踪过程就是以反向解算过程为基础。

双液晶偏振光栅光束偏转示意如图1，两液晶偏振光栅沿光线入射光轴平行放置，以Z轴方向为正方向，当激光光束沿Z轴入射两共轴独立安装的液晶偏振光栅时，入射激光光束皆为圆偏振光，由于激光光束经过两液晶偏振光栅后发生衍射，两液晶偏振光栅旋转角度分别为θ1与θ2，因此发生光束偏转，出射光束高度角为ϕ，方位角为θ。

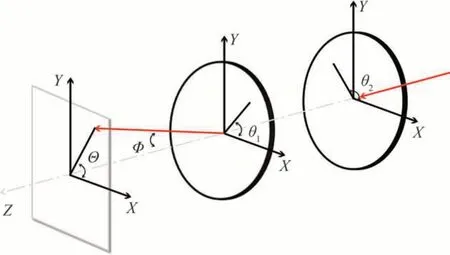
图1 双液晶偏振光栅光束偏转示意Fig. 1 Schematic of dual grating beam deflection

OH C 等［6］建立了在方向余弦空间中两独立旋转平行排列的偏振光栅的衍射模型，该模型可以描述为

式中，K、L、M为出射光束的方向余弦光束方向，λ为光束波长，Λ为光栅周期。出射光束的高度角ϕ和方位角θ可表示为

1.2 反向解算跟踪原理

基于方向余弦空间的反向解算公式是由正向解算公式逆解反推得出。可以由跟踪目标所需的空间偏折角度反向解算出两光栅各自旋转角度，反向解算公式为

也可表示为

机载平台在运动过程中对跟瞄系统会存在姿态扰动，姿态扰动与光轴偏转存在耦合关系，导致跟踪性能下降。由于双液晶偏振光栅光电跟瞄平台独特的光束偏转机制，无法像传统两轴伺服转台一样结合轴上陀螺反馈数据实现载体与目标的相对稳定控制，因此设计双液晶偏振光栅视轴解耦算法（Decoupling Algorithm for Double Grating Axis of Sight，DADG），将视轴解耦算法与双液晶偏振光栅反向解算公式相结合对视轴扰动进行补偿，提高系统性能。根据空间几何关系机载平台扰动与双液晶偏振光栅偏转光轴耦合约束关系可表示为

式中，[ωr ωp ωy]T为惯性测量元件测量姿态角速度，[]T为解算后视轴坐标系下视轴角速度，θx与θy为双液晶偏振光栅的初始出射光束的方位角和俯仰角。首先将机载平台扰动角速度解算到双液晶偏振光栅光束偏转视轴上，其刚体坐标系相对参考坐标系OXoYoZo的转动如图2，然后绕Zo旋转至OXaYaZa，再绕Ya旋转至OXbYbZb，旋转角度分别为θx、θy。

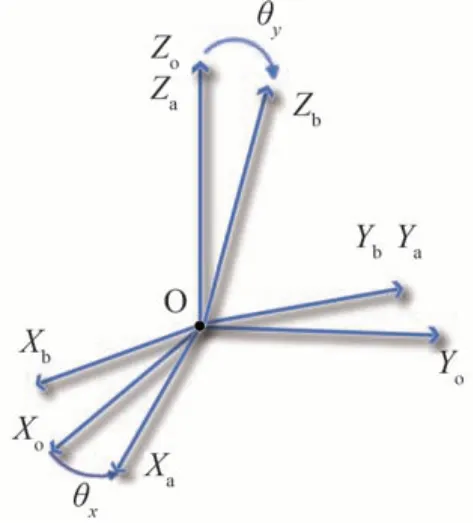
图2 欧拉角角速度解耦示意Fig. 2 Schematic of Euler angular velocity decoupling

解耦矩阵表示为

由于机载平台扰动等因素导致初始出射光束偏离实际目标位置，为了实现双液晶偏振光栅机载平台跟踪功能，将脱靶量与平台姿态信息引入双液晶偏振光栅反向解算公式；引入解耦之后的视轴角速度与图像处理单元输出的目标脱靶量对目标进行跟踪，机载平台下双液晶偏振光栅反向解算跟踪目标位置为

式中，θyaw与θpit为隔离扰动后最终出射光束的方位角与俯仰角，θmx、θmy为根据脱靶量值解算偏离目标的方位、俯仰角度；k1、k2为姿态稳定系数；kx、ky为脱靶量系数。

将跟踪目标空间位置通过极坐标系转换为空间旋转角ϕ'与俯仰角θ'，分别表示为

式中，ϕ'为空间旋转角，θ'为俯仰角。综合上述推导可得出双液晶偏振光栅光电跟踪系统两共轴旋转光栅的旋转角度为

也可表示为

式中，θ1、θ2为两光栅旋转角度，通过系统零点标定得到双液晶偏振光栅视轴坐标系与相机靶面坐标系空间角度偏差θe1、θe2。

2 双液晶偏振光栅控制系统设计

2.1 系统构成

设计了如图3 所示的双液晶偏振光栅光电跟瞄系统，采用两个独立旋转的共轴光栅作为光束偏转执行机构，每个光栅在伺服电机带动下旋转，由编码器测量电机转动位置作为系统反馈，激光光束经过旋转至特定位置的两共轴光栅后衍射，进而发生光束偏转；偏转光束经离轴光学天线、窄带滤波器等器件后进入跟踪相机，相机输出图像数据经图像处理单元反馈光斑目标脱靶量信息；惯性测量单元（Inertial Measurement Unit，IMU）安装于光学系统平台上以反馈平台姿态信息用于系统控制。

图3 双液晶偏振光栅系统构成Fig. 3 Composition of the dual grating system

2.2 控制器设计

双液晶偏振光栅光电跟瞄系统在进行目标跟踪时，需根据当前载体扰动、视轴偏转角度等信息来进行目标跟踪，同时由于双液晶偏振光栅独特的偏转特性需保证两光栅运动控制性能一致。虽然比例积分微分（Proportional Integral Derivative，PID）控制算法应用广泛，对于系统的模型准确度不敏感，但是并不能满足该系统的高精度跟瞄需求，且位置式PID 控制存在积分饱和等问题使其在提升系统跟踪精度以及稳定性等方面存在极大限制。因此，为提高系统跟踪性能设计了一种结合视轴扰动解耦环节的LQR 控制器，双液晶偏振光栅跟瞄系统控制结构如图4。

图4 双液晶偏振光栅控制结构Fig. 4 Dual grating control structure

通过实验与公式原理推导相结合的方法得到系统传递函数。根据现代控制理论将系统传递函数转换为状态空间方程，直流伺服电机数学模型为

现代控制理论状态空间方程建模一般模型为

式中

设计全状态反馈控制器，令u(t)=-Kz(t)，可得，则该系统闭环矩阵为Acl1=A-BK，其中K=[k1k2k3] 。

闭环系统的闭环状态矩阵特征值决定了闭环系统的控制表现，为了更好地选择闭环矩阵特征值引入代价函数J，通过求解Jmin得到闭环矩阵特征值，进而得出全状态反馈控制器反馈系数矩阵K。矩阵Q和矩阵R分别是状态变量和动态系统输入量的权重矩阵，两矩阵皆为正定的对称矩阵。该系统为三状态单输入系统，则

权重系数的不同意味着对不同空间状态变量的关注度不同，通过综合电机性能、控制精度、输入能耗等各方面因素确定权重参数，保证闭环系统在电机额定参数内达到稳定的快速收敛状态。在系统构建过程中，环路电流反馈值不能直接获得，为使动态系统闭环需要引入观测器对系统的电流进行观测。根据现代控制理论分析，该系统满足可观测性，状态观测器的状态空间方程为

式中，L=[l1l2l3]，观测误差为，则观测器观测误差z͂(t)平衡点为[0]，观测器闭环矩阵为Acl2=A-CL。通过闭环矩阵特征值的选取对L进行参数配置使观测器收敛速度为LQR 控制器收敛速度的两倍，以保证LQR 控制器的设计基于一个最优的观测值上。

3 实验及结果分析

为验证基于双液晶偏振光栅的光电跟瞄系统的跟踪性能进行动态跟踪实验，搭建了双液晶偏振光栅光电跟瞄系统跟踪性能检测系统，液晶偏振光栅有效口径为50 mm，离轴反射系统波像差均方根值（Root Mean Square，RMS）统计小于λ/12，选择入射光波段为λ=1 053 mm，光学天线镀膜后，对1 053 nm 激光光束反射率大于99.95%。根据上述参数设置双液晶偏振光栅系统最大光束偏转角度为±15°。由于该系统针对1 053 nm 波长激光光束进行设计，考虑不同波段光束经过液晶偏振光栅系统后传播方向会发生不同程度的变化，因此在光学窗口镀增透膜、光学天线主次镜镀增反膜以提高对应波段光束接收效率，后续加窄带滤光片滤除杂散光，选择窄线宽激光器根据激光中心波长对镀膜透射波段和带宽进行匹配优化，以最大程度削弱光束波长变化对镀膜效果的影响。在双液晶偏振光栅系统运动控制中选择STM32F4 系列MCU 作为运动控制主控单元，通过绝对式编码器采集到的光栅旋转角度数据作为反馈来设计伺服闭环系统，系统采样频率为1 000 Hz，最终的测试结果通过式（26）进行计算。

式中，δ为双液晶偏振光栅光电跟瞄系统RMS 统计跟踪精度，单位为μrad；Xi与Yi为跟踪光斑中心位置的方位与俯仰脱靶量，单位为μrad；Xˉ与Yˉ为光斑中心位置的方位与俯仰脱靶量均值，单位为μrad；N为数据记录次数。双液晶偏振光栅跟踪视场如图5。

图5 双液晶偏振光栅跟踪视场图像Fig. 5 Dual grating tracking field of view image

为了测试双液晶偏振光栅光电跟踪平台在跟踪区域内的跟踪性能，将光电跟踪平台放置于六自由度摇摆台上，将3 m 焦距平行光管对准跟踪平台，由平行光管后方激光器出射波长为1 053 nm 激光，光束经平行光管后射出，以模拟远距离目标，如图6。

图6 系统跟踪实验现场Fig. 6 System tracking experiment site long-distance targets and tracking field of view

近似平行光射入双液晶偏振光栅光端机内，双液晶偏振光栅光端机捕获光斑进行跟踪，摇摆台分别在绕X轴与绕Z轴方向同时进行摆动，摆动幅度分别为2°@0.5 Hz 与5°@0.2 Hz，两轴正弦运动相位相差90°。惯性测量单元采集的平台姿态数据如图7、图8。

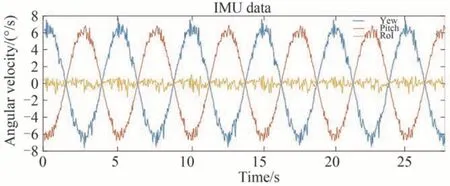
图7 IMU 采集5°@0.2 Hz 扰动下姿态数据Fig. 7 Acquisition of attitude data under 5°@0.2 Hz disturbance

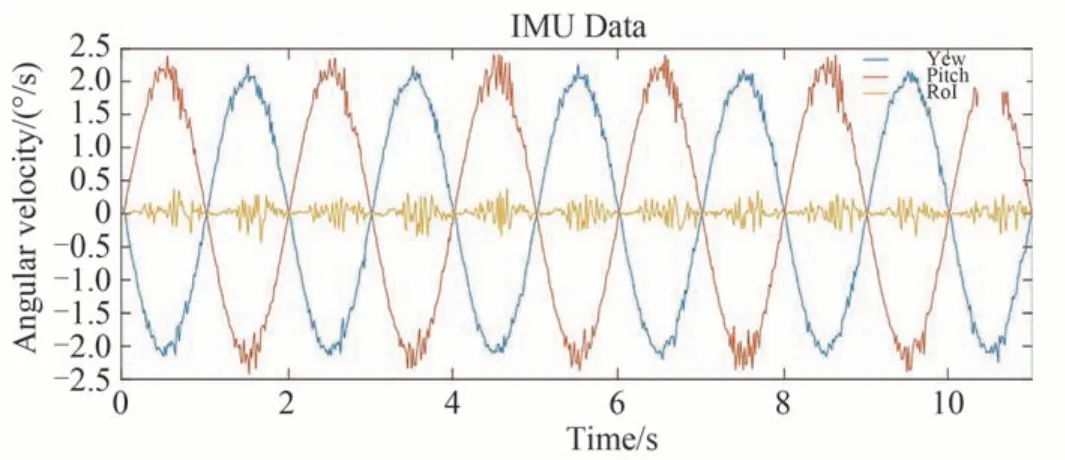
图8 IMU 采集2°@0.5 Hz 扰动下姿态数据Fig. 8 Acquisition of attitude data under 2°@0.5Hz disturbance

通过动态实验结果对比，在双轴5°@0.2 Hz 扰动的情况下，LQR 与视轴解耦相结合算法对光电跟踪系统的跟踪性能有显著提升。应用LQR 算法后与PID 算法相比，系统方位坐标脱靶量峰峰值下降30%，俯仰坐标脱靶量峰峰值下降30.86%；应用LQR+DADG 算法后与PID 算法相比，系统方位坐标脱靶量峰峰值下降47.8%，俯仰坐标脱靶量峰峰值下降45.26%。在双轴2°@0.5 Hz 扰动的情况下，应用LQR 算法后与PID 算法相比，系统方位坐标脱靶量峰峰值下降31.24%，俯仰坐标脱靶量峰峰值下降28.2%；应用LQR+DADG算法后与PID 算法相比，系统方位坐标脱靶量峰峰值下降43.49%，俯仰坐标脱靶量峰峰值下降42.06%。

通过上位机记录方位、俯仰脱靶量数据3 000 个，进行双轴脱靶量数据RMS 计算，加入LQR 与视轴解耦算法后在2°@0.5 Hz 与5°@0.2 Hz 扰动情况下双轴脱靶量RMS 统计数值分别为 328 μrad 与289 μrad。通过实验验证将PID 参数调整为最佳状态，保证其快速性的前提下将阶跃响应超调量优化为4.54%，参数分别为Kp=53.2、Ki=0.3、Kd=4.88。应用PID 算法时双轴脱靶量RMS 统计数值分别为632 μrad 与503 μrad，系统跟踪残差结果如图9、图10，故应用LQR 与视轴解耦算法后与PID 跟踪算法相比系统跟踪性能得到明显提升。

图9 2°@0.5 Hz 扰动下跟踪残差图Fig. 9 Tracking residual plot at 2°@0.5 Hz perturbation

图10 5°@0.2 Hz 扰动下跟踪残差图Fig. 10 Tracking residual plot at 2°@0.5 Hz perturbatio

4 结论

通过开展基于视轴解耦与LQR 算法结合的双液晶偏振光栅光电跟踪平台跟踪性能研究，建立了视轴解耦与双液晶偏振光栅反向解算相结合的光束偏转模型，推导了双液晶偏振光栅视轴解耦过程并将结果引入双液晶偏振光栅反向解算公式，设计了基于LQR 最优控制理论的双液晶偏振光栅控制器，实现了机载扰动下对目标的高精度跟踪，将液晶偏振光栅光束偏转技术在机载激光通信等工程技术应用中做进一步拓展。搭建了跟踪功能验证实验，对基于视轴解耦与LQR 控制器的双液晶偏振光栅跟踪平台进行了实验验证，实验结果表明，改进后算法相比传统PID 算法双液晶偏振光栅跟瞄系统方位与俯仰轴实时跟踪精度均提升了40%以上，达到了双轴脱靶量RMS 统计小于350 μrad 的指标，跟踪精度得到极大提升；该精度下的双液晶偏振光栅跟瞄系统作为粗跟踪环路时其方位轴与俯仰轴扫描范围均为±15°，满足轻量型机载平台对光电跟瞄设备的使用需求；可以将光斑稳定在精跟踪视场内，满足粗精复合跟瞄系统中粗跟踪环路精度需求。通过实验证明了双液晶偏振光栅光电跟瞄系统的优异性，验证了LQR 控制理论与视轴解耦算法相结合的正确性与有效性，为基于双液晶偏振光栅的新型光电跟瞄技术的发展提供了实验参考与理论支持。后续研究工作将继续对机载平台下的双液晶偏振光栅光电跟踪系统进行改进，优化系统跟踪性能。针对双液晶偏振光栅光束指向两光栅旋转位置与光束偏折角度的非线性关系，将继续优化系统结构，改进控制算法，选取更优性能的探测器以进一步提高跟瞄精度。